HDU

传送门：http://acm.hdu.edu.cn/showproblem.php?pid=6158

本题是一个计算几何题——四圆相切。

平面上的一对内切圆，半径分别为R和r。现在这一对内切圆之间，按照如图所示的方式依次放置N个相切的圆。求放置的这N个圆的面积之和。

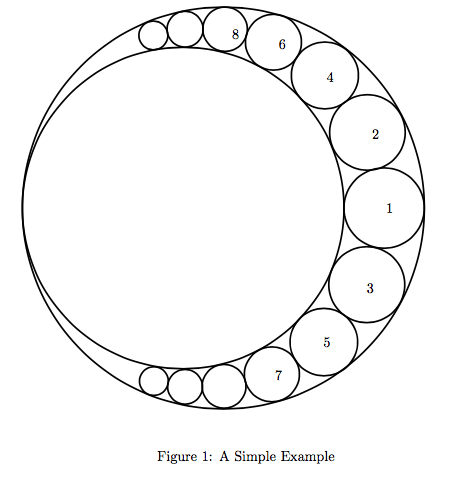
在此，首先介绍一个定理：笛卡尔定理。Wiki: Descartes' theorem。

平面上的四个圆，第i个圆的半径为r[i]，曲率为κ[i]（注：κ=r­^-1）。若这四个圆中的每一对均构成外切，则其曲率满足约束：

$left(sum_{i=1}^4 kappa _i ight)^2 = 2cdot sum_{i=1}^4 kappa _i^2$

通过这个定理，可以得到以下情景相应的约束：

平面上的三个圆，第i个圆的半径为r[i]，曲率为κ[i]。若这三个圆中的每一对均构成外切，且同时内切于一个半径为R，曲率为K的大圆，则其曲率同样满足以上的关系（注：此处大圆的曲率应取负值，即K=-R^-1）。半径的约束式相应地写成：

$left(sum_{i=1}^3 kappa _i -frac{1}{R} ight)^2 = 2left( sum_{i=1}^3 kappa _i^2+frac{1}{R^2} ight)$

接下来，首先考虑上半侧的情况（下半侧与之对称）。设上半侧放置的第k个圆的曲率为c[k]（约定放置于中间的圆的曲率为c[0]），则其与半径为r的圆、放置的第k-1个圆相外切，并同时内切于半径为R的圆。根据四圆相切的关系写出约束式：

$left(frac{1}{r}-frac{1}{R} +c_k+c_{k-1} ight)^2 = 2left(frac{1}{r^2}+frac{1}{R^2} +c_k^2+c_{k-1}^2 ight)$

相应地考虑第k+1个圆，则有：

$left(frac{1}{r}-frac{1}{R} +c_k+c_{k+1} ight)^2 = 2left(frac{1}{r^2}+frac{1}{R^2} +c_k^2+c_{k+1}^2 ight)$

两式相减，则有：

$(c_{k+1}-c_{k-1})left( 2frac{R-r}{Rr}+2c_k+c_{k+1}+c_{k-1} ight )=2(c_{k+1}+c_{k-1})(c_{k+1}-c_{k-1})\Rightarrow 2frac{R-r}{Rr}+2c_k=c_{k+1}+c_{k-1}Rightarrow (c_{k+1}-c_k)-(c_k-c_{k-1})=2frac{R-r}{Rr}$

设d[k]=c[k]-c[k-1]，则d[]是一个等差数列。为求得这个等差数列，首先需要求解首项。

c[0]是显然的，而c[1]则可以借助与R、r、c[0]的关系求解。

$c_0=frac{1}{R-r}\c_1=frac{R^2+r^2-Rr}{Rr(R-r)}$

于是，d[]的通项公式：$d_k=(2k-1)frac{R-r}{Rr},k=1,2,3,cdots$

于是，c[]的通项公式：$c_k=frac{1}{R-r}+frac{R-r}{Rr}k^2,k=0,1,2,3,cdots$

求解时注意精度控制。参考程序如下：

#include <bits/stdc++.h>
using namespace std;

const double pi = acos(-1);
const double eps = 1e-14;

int R, r;
double a, b;

double get_curv(int k)
{
    return a + b * k * k;
}

int main(void)
{
    int t;
    scanf("%d", &t);
    while (t--) {
        int n;
        scanf("%d%d%d", &R, &r, &n);
        if (R == r) {
            printf("%.5f
", 0);
            continue;
        }
        if (R < r) swap(R, r);
        a = 1.0 / (R - r);
        b = 1.0 * (R - r) / (R * r);
        //Add first circle.
        int rad = 1.0 / get_curv(0);
        double ans = rad * rad;
        //Add following circles.
        for (int i = 2; i <= n; i += 2) {
            double rad = 1.0 / get_curv(i / 2);
            double ds = rad * rad;
            if (ds < eps) break;
            ans += ds * (i < n ? 2 : 1);
        }
        printf("%.5f
", ans * pi);
    }
    return 0;
}

本题还有一种更为简单的解法，即通过笛卡尔定理与韦达定理进行迭代。参考程序如下：

#include <bits/stdc++.h>
using namespace std;

const double pi = acos(-1);
const double eps = 1e-14;

int R, r;

int main(void)
{
    int t;
    scanf("%d", &t);
    while (t--) {
        int n;
        scanf("%d%d%d", &R, &r, &n);
        if (R == r) {
            printf("%.5f
", 0);
            continue;
        }
        if (R < r) swap(R, r);
        //Add first circle.
        double ans = (R - r) * (R - r);
        double k_1 = -1.0 / R;
        double k_2 = 1.0 / r;
        double k_3 = 1.0 / (R - r);
        double k_4 = k_1 + k_2 + k_3;
        //Add following circles.
        for (int i = 2; i <= n; i += 2) {
            double ds = 1.0 / (k_4 * k_4);
            if (ds < eps) break;
            ans += ds * (i < n ? 2 : 1);
            double k_5 = 2.0 * (k_1 + k_2 + k_4) - k_3;
            k_3 = k_4;
            k_4 = k_5;
        }
        printf("%.5f
", ans * pi);
    }
    return 0;
}