HMM学习 viterbi算法1

维特比算法（Viterbi Algorithm）

寻找最可能的隐藏状态序列(Finding most probable sequence of hidden states)。
对于一个特殊的隐马尔科夫模型(HMM)及一个相应的观察序列，我们常常希望能找到生成此序列最可能的隐藏状态序列。

穷举搜索

　　我们使用下面这张网格图片来形象化的说明隐藏状态和观察状态之间的关系：

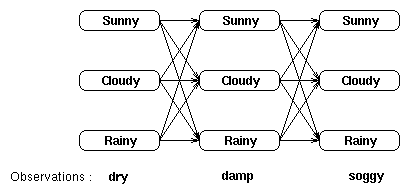
　　我们可以通过列出所有可能的隐藏状态序列并且计算对于每个组合对应的观察序列的概率来找到最可能的隐藏状态序列。最可能的隐藏状态序列是使下面这个概率最大的组合:
　　　　　　

P r （ 观 察 序 列 | 隐 藏 状 态 的 组 合 ）

　　例如，对于网格中所显示的观察序列，最可能的隐藏状态序列是下面这些概率中最大概率所对应的那个隐藏状态序列：
　　

P r (d r y, d a m p, s o g g y | s u n n y, s u n n y, s u n n y), P r (d r y, d a m p, s o g g y | s u n n y, s u n n y, r a i n y), . . . . P r (d r y, d a m p, s o g g y | r a i n y, r a i n y, r a i n y)

　　这种方法是可行的，但是通过穷举计算每一个组合的概率找到最可能的序列是极为昂贵的。与前向算法类似，我们可以利用这些概率的时间不变性来降低计算复杂度。

使用递归降低复杂度

给定一个观察序列和一个隐马尔科夫模型（HMM），我们将考虑递归地寻找最有可能的隐藏状态序列。我们首先定义局部概率 $δ$ ,它是到达网格中的某个特殊的中间状态时的概率。然后，我们将介绍如何在t=1和t=n(>1)时计算这些局部概率。这些局部概率与前向算法中所计算的局部概率是不同的，因为它们表示的是时刻t时到达某个状态最可能的路径的概率，而不是所有路径概率的总和。

局部概率 $δ$ 和局部最佳途径

考虑下面这个网格，它显示的是天气状态及对于观察序列干燥，湿润及湿透的一阶状态转移情况：

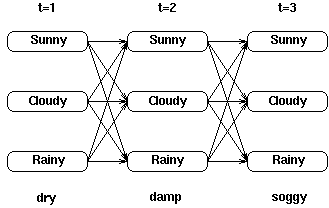
对于网格中的每一个中间及终止状态，都有一个到达该状态的最可能路径。举例来说，在t=3时刻的3个状态中的每一个都有一个到达此状态的最可能路径，或许是这样的：

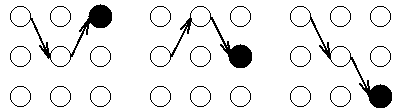
我们称这些路径为局部最佳路径(partial best paths)。其中每个局部最佳路径都有一个相关联的概率，即局部概率或

δ

。与前向算法中的局部概率不同，

δ

是到达该状态（最可能）的一条路径的概率。
因而 $δ (i, t)$ 是t时刻到达状态i的所有序列概率中最大的概率，而局部最佳路径是得到此最大概率的隐藏状态序列。对于每一个可能的i和t值来说，这一类概率（及局部路径）均存在。
　　特别地，在t=T时每一个状态都有一个局部概率和一个局部最佳路径。这样我们就可以通过选择此时刻包含最大局部概率的状态及其相应的局部最佳路径来确定全局最佳路径（最佳隐藏状态序列）。

计算t=1时刻的局部概率 $δ$

　我们计算的局部概率 $δ$ 是作为最可能到达我们当前位置的路径的概率（已知的特殊知识如观察概率及前一个状态的概率）。当t=1的时候，到达某状态的最可能路径明显是不存在的；但是，我们使用t=1时的所处状态的初始概率及相应的观察状态k1的观察概率计算局部概率 $δ$ ；即
　

δ_{1} (i) = π (i) b_{i k_{1}}

与前向算法类似，这个结果是通过初始概率

π

和相应的观察概率

b

相乘得出的。

计算t>1时刻的局部概率 $δ$

利用t-1时刻的局部概率 $δ$ 计算t时刻的局部概率 $δ$ ?
考虑如下的网格：

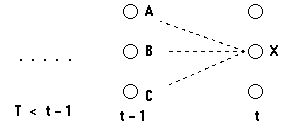
　我们考虑计算t时刻到达状态X的最可能的路径；这条到达状态X的路径将通过t-1时刻的状态A，B或C中的某一个。因此，最可能的到达状态X的路径将是下面这些路径的某一个
　　　　　　　（状态序列），…，A，X
　　　　　　　（状态序列），…，B，X
或　　　　　　（状态序列），…，C，X
我们想找到路径末端是AX,BX或CX并且拥有最大概率的路径。
回顾一下马尔科夫假设：给定一个状态序列，一个状态发生的概率只依赖于前n个状态。特别地，在一阶马尔可夫假设下，状态X在一个状态序列后发生的概率只取决于之前的一个状态，即

P r (到 达 状 态 A 最 可 能 的 路 径) . P r (X | A) . P r (观 察 状 态 | X)

与此相同，路径末端是AX的最可能的路径将是到达A的最可能路径再紧跟X。相似地，这条路径的概率将是：

P r (到 达 状 态 A 最 可 能 的 路 径) . P r (X | A) . P r (观 察 状 态 | X)

　因此，到达状态X的最可能路径概率是：

fig5

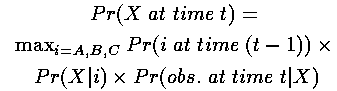
其中第一项是t-1时刻的局部概率

δ

，第二项是状态转移概率以及第三项是观察概率。泛化上述公式，就是在t时刻，观察状态是kt，到达隐藏状态i的最佳局部路径的概率是：

fig6

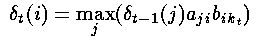
这里，我们假设前一个状态（局部概率）是已知的，同时利用了状态转移概率和相应的观察概率之积。然后，我们就可以在其中选择最大的概率了（局部概率

δ

）。

反向指针

　考虑下面这个网格，在每一个中间及终止状态我们都知道了局部概率 $δ (i, t)$ 。然而我们的目标是在给定一个观察序列的情况下寻找网格中最可能的隐藏状态序列——因此，我们需要一些方法来记住网格中的局部最佳路径。

回顾一下我们是如何计算局部概率的，计算t时刻的

δ

我们仅仅需要知道t-1时刻的

δ

。在这个局部概率计算之后，就有可能记录前一时刻哪个状态生成了

d e l t a (i, t)

——也就是说，在t-1时刻系统必须处于某个状态，该状态导致了系统在t时刻到达状态i是最优的。这种记录（记忆）是通过对每一个状态赋予一个反向指针

ϕ

完成的，这个指针指向最优的引发当前状态的前一时刻的某个状态。
形式上，我们可以写成如下的公式,其中argmax运算符是用来计算使括号中表达式的值最大的索引

j

的。

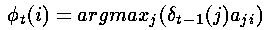
　　这个表达式是通过前一个时间步骤的局部概率和转移概率计算的，并不包括观察概率（与计算局部概率本身不同）。这是因为我们希望这些

ϕ

能回答这个问题“如果我在这里，最可能通过哪条路径到达下一个状态？”——这个问题与隐藏状态有关，因此与观察概率有关的混淆（矩阵）因子是可以被忽略的。

维特比算法的优点

使用Viterbi算法对观察序列进行解码有两个重要的优点：
　　1. 通过使用递归减少计算复杂度——这一点和前向算法使用递归减少计算复杂度是完全类似的。
　　2.维特比算法有一个非常有用的性质，就是对于观察序列的整个上下文进行了最好的解释（考虑）。事实上，寻找最可能的隐藏状态序列不止这一种方法，其他替代方法也可以，譬如，可以这样确定如下的隐藏状态序列：

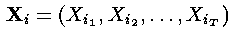
其中

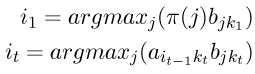
这里，采用了“自左向右”的决策方式进行一种近似的判断，其对于每个隐藏状态的判断是建立在前一个步骤的判断的基础之上（而第一步从隐藏状态的初始向量 $π$ 开始）。
这种做法，如果在整个观察序列的中部发生“噪音干扰”时，其最终的结果将与正确的答案严重偏离。相反，维特比算法在确定最可能的终止状态前将考虑整个观察序列，然后通过 $ϕ$ 指针“回溯”以确定某个隐藏状态是否是最可能的隐藏状态序列中的一员。这是非常有用的，因为这样就可以孤立序列中的“噪音”，而这些“噪音”在实时数据中是很常见的。

小结

　　维特比算法提供了一种有效的计算方法来分析隐马尔科夫模型的观察序列，并捕获最可能的隐藏状态序列。它利用递归减少计算量，并使用整个序列的上下文来做判断，从而对包含“噪音”的序列也能进行良好的分析。
　　在使用时，维特比算法对于网格中的每一个单元(cell)都计算一个局部概率，同时包括一个反向指针用来指示最可能的到达该单元的路径。当完成整个计算过程后，首先在终止时刻找到最可能的状态，然后通过反向指针回溯到t=1时刻，这样回溯路径上的状态序列就是最可能的隐藏状态序列了。

转自：“我爱自然语言处理”：www.52nlp.cn
链接：http://www.52nlp.cn/hmm-learn-best-practices-six-viterbi-algorithm-1
译自：http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html