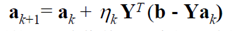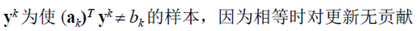讨论前提:两类,线性可分(广义判别函数意义下)
准备工作:样本规范化(如果样本集是线性可分的,将属于类别2 的所有样本由 y变成 –y,对所有 n 样本,将得到 aTy>0)
样本增广(将所有样本写成齐次坐标形式,即 y = (x',1) ,把n维样本加上阈值构成n+1维的样本)
求解:
对应每个样本yi ,通过令a' * yi=0,可以得到一个超平面,n个样本将得到n个超平面,它们的正半空间的交集区域内存在解向量。
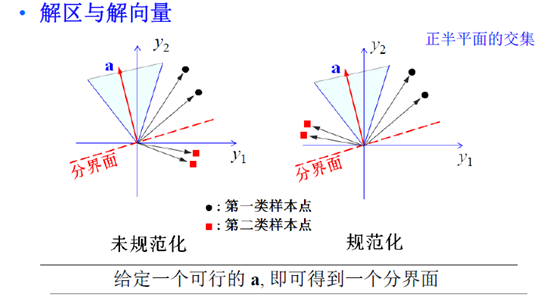
问题出现在无论这个交集有多大,只要样本线性可分,总是会存在无穷多个候选的a,我们要取用哪一个。
这就需要一个准则来判断a的好坏:

这里由于y分错了,a*y就会小于零,换而言之,这个J(a)总是大于等于零的,就训练样本而言我们当然希望他是零,也就是不存在错分点。
接下来的问题就是要最小化J(a).
使用的算法是梯度下降法:
参数更新值 = 参数当前值 - 迭代步长 * 目标函数的梯度 。
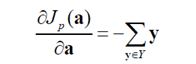
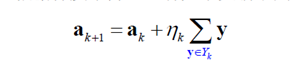

图形化解释上面的过程,就是不断的改变a的方向以使得错分样本能够进入正半空间。
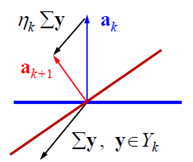
判断a如何的准则不止一个,又如:
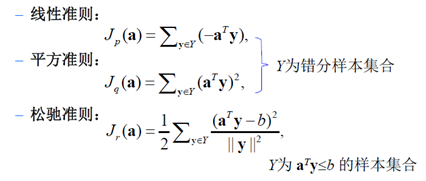
综合来讲,松弛准则会更好一点,克服了梯度不连续(线性准则),与下降过慢(平方准则)等缺点。
最小平方误差(MSE)准则函数
过去的目标是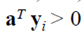 ,现在改成
,现在改成
这样子的好处是:将n个样本得到的n个不等式规划问题,转换成了n个等式的联合求解过程(即解方程组)。
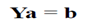
由于样本个数要大于空间维数,所以Y通常不可逆,所以我们要评价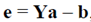 ,解得a使得e最小。
,解得a使得e最小。
准则是
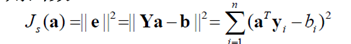
求偏导数得:
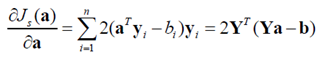
想求得偏导数等于零的点,由于高维中的伪逆并不好求,所以常用梯度下降进行处理: