树状数组(用于每次只修改一个值的区间查询)
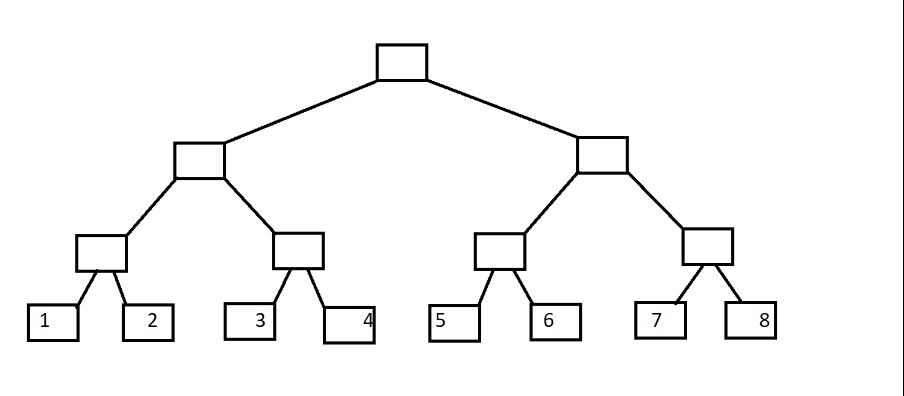
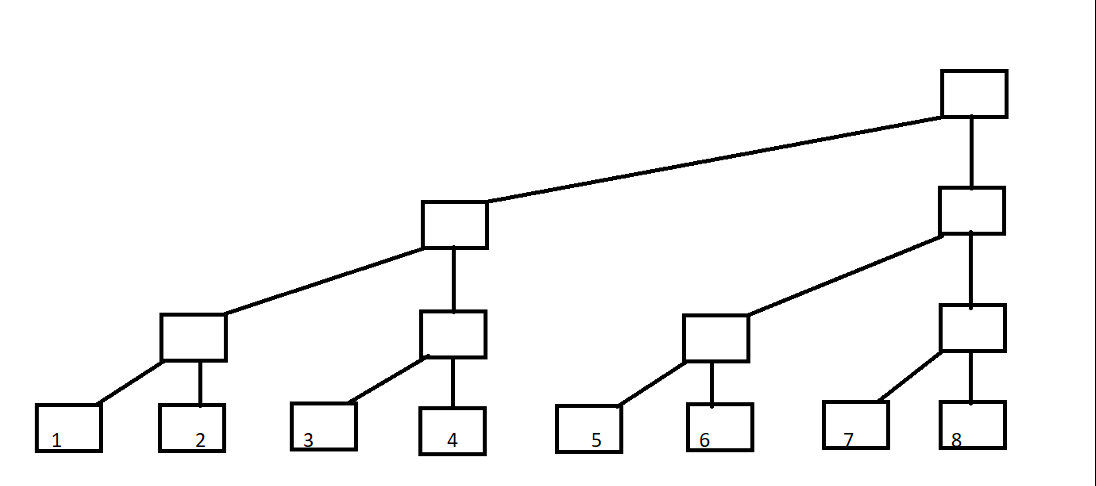
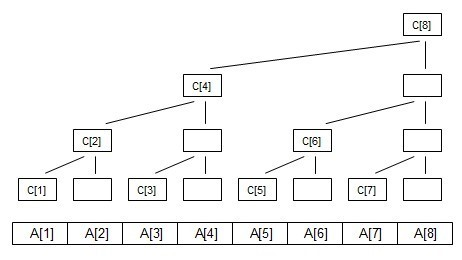
这里A[] 是原数组,C[] 就是树状数组了。
由演变过程来看,这里运用了二分的思想。设节点编号为x,那么这个节点所管理的区间长度为 2^k (k为x二进制末尾0的个数)。所以 Cn = A(n - 2^k + 1) + ... + An
关于Lowbit(x) ,这里返回的是 x 用二进制表示时,最低位的1所表示的数,例如x的二进制1100100,返回的是100,就是十进制的4,也就是c[x]所管理的区间长度
感觉结合图跟模板不难懂
int n, m, a[MAXN], c[MAXN << 1]; //计算该点所管理的区间长度 2 ^ k int Lowbit(int x) { return x & (-x); } //修改 void change(int x, int num) { while(x <= n) { c[x] += num; x += Lowbit(x); } } //查询 int sum(int x) { int ans = 0; while(x > 0) { ans += c[x]; x -= Lowbit(x); }
return ans; }
线段树
本文参考这篇(By 岩之痕)膜拜大佬
目录
1、线段树的简单操作(建树,点修改,查询)
2、区间修改(区间都加上 num, 区间都变成 num)
3、非递归线段树(此部分为原文加以排版以及我个人理解,写得真不错)

上图就是线段树的样子,给个简单的解释,例如这棵树是求区间和的话,那个 [1, 10]算的就是 [1, 10]的和
1、线段树的简单操作(建树,点修改,查询)
//建树,rt代表根,这里不懂的话手动结合上图模拟,从根开始 void Build(int l, int r, int rt) { if(l == r) { scanf("%d", &sum[rt]); return ; } int m = (l + r) >> 1; Build(l, m, rt << 1); Build(m + 1, r, rt << 1 | 1); //更新sum sum[rt] = sum[rt << 1] + sum[rt << 1 | 1]; }
//修改,设原数组为 a ,即为 a[x] += num void Update(int x, int num, int l, int r, int rt) { if(l == r) { sum[rt] += num; return ; } int m = (l + r) >> 1; //看 x 在左区间还是右区间 if(x <= m) Update(x, num, l, m, rt << 1); else Update(x, num, m + 1, r, rt << 1 | 1); sum[rt] = sum[rt << 1] + sum[rt << 1 | 1]; }
//查询 int Query(int L, int R, int l, int r, int rt) { if(L <= l && r <= R) return sum[rt]; int m = (l + r) >> 1; int ans = 0; if(L <= m) ans += Query(L, R, l, m, rt << 1);//左子区间与[L, R]有重叠 if(R > m) ans += Query(L, R, m + 1, r, rt << 1 | 1); return ans; }
上题题解

#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <sstream> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <iomanip> #include <stack> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int MAXN = 50005; const int MOD = 1e9 + 7; #define MemI(x) memset(x, -1, sizeof(x)) #define Mem0(x) memset(x, 0, sizeof(x)) #define MemM(x) memset(x, 0x3f, sizeof(x)) #define lson l, m, rt << 1 #define rson m + 1, r, rt << 1 | 1 int sum[MAXN << 2]; //建树,rt代表根,这里不懂的话手动结合上图模拟,从根开始 void Build(int l, int r, int rt) { if(l == r) { scanf("%d", &sum[rt]); return ; } int m = (l + r) >> 1; Build(l, m, rt << 1); Build(m + 1, r, rt << 1 | 1); //更新sum sum[rt] = sum[rt << 1] + sum[rt << 1 | 1]; } //修改,设原数组为 a ,即为 a[x] += num void Update(int x, int num, int l, int r, int rt) { if(l == r) { sum[rt] += num; return ; } int m = (l + r) >> 1; //看 x 在左区间还是右区间 if(x <= m) Update(x, num, l, m, rt << 1); else Update(x, num, m + 1, r, rt << 1 | 1); sum[rt] = sum[rt << 1] + sum[rt << 1 | 1]; } //查询 int Query(int L, int R, int l, int r, int rt) { if(L <= l && r <= R) return sum[rt]; int m = (l + r) >> 1; int ans = 0; if(L <= m) ans += Query(L, R, l, m, rt << 1);//左子区间与[L, R]有重叠 if(R > m) ans += Query(L, R, m + 1, r, rt << 1 | 1); return ans; } int main() { int T; scanf("%d", &T); for(int cas = 1;cas <= T;++cas) { printf("Case %d: ", cas); int n; scanf("%d", &n); Build(1, n, 1); char s[15]; while(1) { scanf("%s", s); int x, y; if(s[0] == 'A') { scanf("%d%d", &x, &y); Update(x, y, 1, n, 1); } else if(s[0] == 'S') { scanf("%d%d", &x, &y); Update(x, -y, 1, n, 1); } else if(s[0] == 'Q') { scanf("%d%d", &x, &y); printf("%d ", Query(x, y, 1, n, 1)); } else break; } } return 0; }
后面一些线段树的具体题目,链接就不贴了。
2、区间修改(区间都变成 num,区间都加上num)
(1)区间都变成num
我这里定义了一个 book[] 数组作为标记, book[] 也是线段树,在这里存的是修改的值,则代表某一区间的 sum[x] = book[x] * (r - l + 1),这里基本上book[] 就照这个公式存值。如果 book[x] 被标记了,就代表该区间的值已经改变了,同时我们把 sum[x] 的值进行修正,但是!此时该区间的子区间的值没有被修正(对查询操作没有影响,已经得到所要区间的值sum[x])!之后,如果遍历该区间已经被标记了的话,就把该区间的两个子区间进行标记,同时去掉改区间的标记。(延迟下推,直到遍历到该区间才下推)
void Update(int L, int R, int num, int l, int r, int rt) { if(L <= l && r <= R) { sum[rt] = num * (r - l + 1); book[rt] = num; return ; } int m = (l + r) >> 1; //看这个区间有没有被标记,延迟下推 PushDown(rt, m - l + 1, r - m); if(L <= m) Update(L, R, num, lson); if(R > m) Update(L, R, num, rson); PushUp(rt); } void PushDown(int rt, int ln, int rn) { if(book[rt]) { //标记下推到该区间的两个子区间,同时删除该标记 book[rt << 1] = book[rt << 1 | 1] = book[rt]; sum[rt << 1] = ln * book[rt << 1]; sum[rt << 1 | 1] = rn * book[rt << 1 | 1]; book[rt] = 0; } }
(2)区间都加上num
这个跟上面类似,上述代码稍微修改一下即可,此时book[] 代表的是增加值
POJ-3468
跟上面模板的不同:PushUp() 里面用的是 +=;
Update()里面用的是 +=;
Query()里面加了PushDown(),不加会错,因为查询的时候可能会下推标记区间

#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <sstream> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <iomanip> #include <stack> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int MAXN = 100005; const int MOD = 1e9 + 7; #define MemI(x) memset(x, -1, sizeof(x)) #define Mem0(x) memset(x, 0, sizeof(x)) #define MemM(x) memset(x, 0x3f, sizeof(x)) #define lson l, m, rt << 1 #define rson m + 1, r, rt << 1 | 1 LL sum[MAXN << 2], book[MAXN << 2]; void PushUp(int rt) { sum[rt] = sum[rt << 1] + sum[rt << 1 | 1]; } void PushDown(int rt, int ln, int rn) { if(book[rt]) { book[rt << 1] += book[rt]; book[rt << 1 | 1] += book[rt]; sum[rt << 1] += book[rt] * ln; sum[rt << 1 | 1] += book[rt] * rn; book[rt] = 0; } } void Build(int l, int r, int rt) { if(l == r) { scanf("%lld", &sum[rt]); return ; } int m = (l + r) >> 1; Build(lson); Build(rson); PushUp(rt); } void Update(int L, int R, int num, int l, int r, int rt) { if(L <= l && r <= R) { sum[rt] += num * (r - l + 1); book[rt] += num; return ; } int m = (l + r) >> 1; PushDown(rt, m - l + 1, r - m); if(L <= m) Update(L, R, num, lson); if(R > m) Update(L, R, num, rson); PushUp(rt); } LL Query(int L, int R, int l, int r, int rt) { if(L <= l && r <= R) return sum[rt]; int m = (l + r) >> 1; LL ans = 0; PushDown(rt, m - l + 1, r - m); if(L <= m) ans += Query(L, R, lson); if(R > m) ans += Query(L, R, rson); return ans; } int main() { Mem0(book); Mem0(sum); int n, q; scanf("%d%d", &n, &q); Build(1, n, 1); char c[5]; int l, r, num; while(q--) { scanf("%s%d%d", &c, &l, &r); if(c[0] == 'Q') printf("%lld ", Query(l, r, 1, n, 1)); else { scanf("%d", &num); Update(l, r, num, 1, n, 1); } } return 0; }
这里再贴出参考博客的解释,他的 Add[] 如同我的 book[]
线段树的区间修改也是将区间分成子区间,但是要加一个标记,称作懒惰标记。
3、非递归线段树(此部分为原文加以排版以及我个人理解。。。)
(1)点修改:
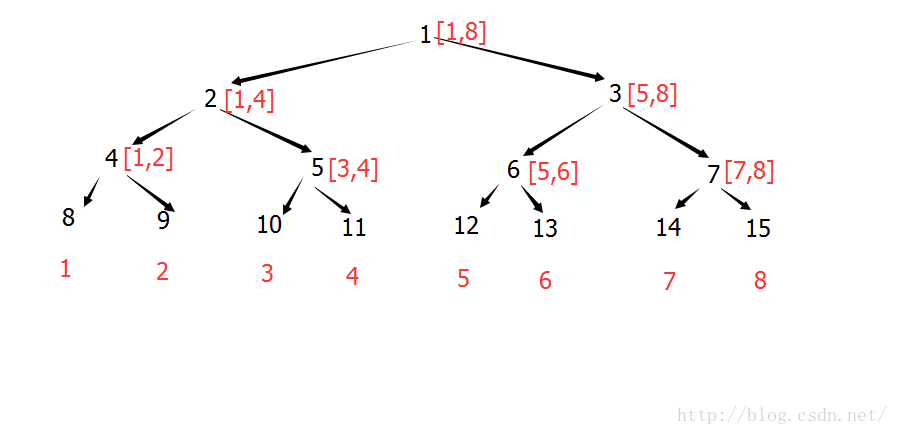
(2)点修改下的区间查询:
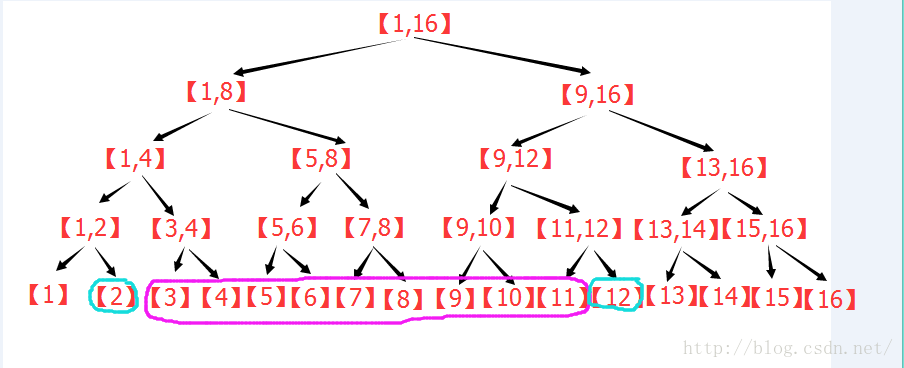
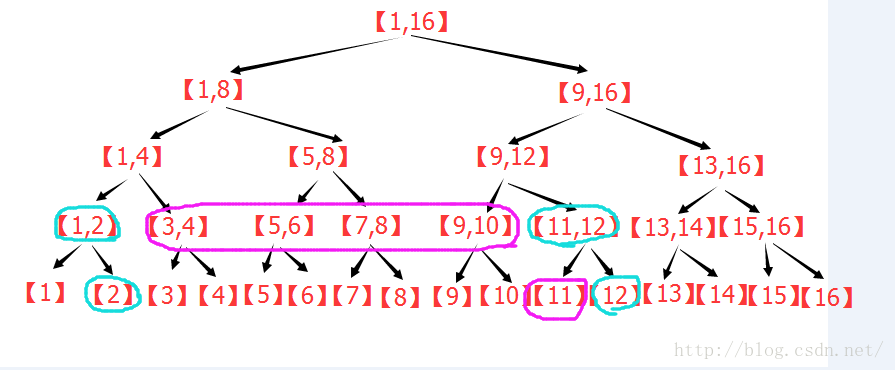
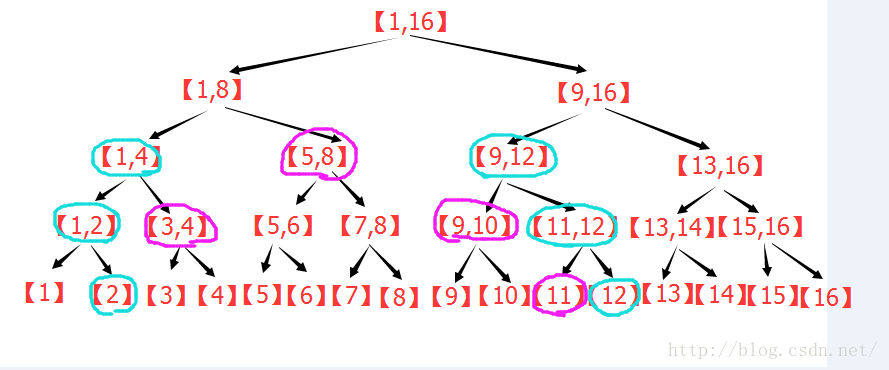
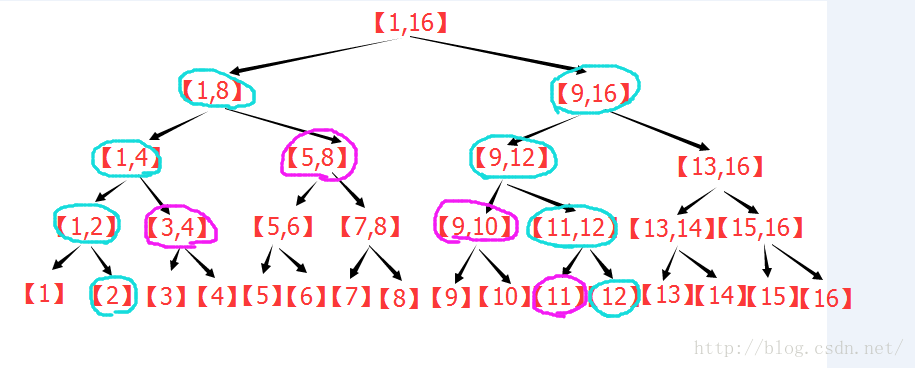

(3)区间修改下的区间查询:

(4)区间修改:
(5)非递归实现
(0)定义:
#define maxn 100007 int A[maxn],n,N;//原数组,n为原数组元素个数 ,N为扩充元素个数 int Sum[maxn<<2];//区间和 int Add[maxn<<2];//懒惰标记
(1)建树:
void Build(int n){ //计算N的值 N=1;while(N < n+2) N <<= 1; //更新叶节点 for(int i=1;i<=n;++i) Sum[N+i]=A[i];//原数组下标+N=存储下标 //更新非叶节点 for(int i=N-1;i>0;--i){ //更新所有非叶节点的统计信息 Sum[i]=Sum[i<<1]+Sum[i<<1|1]; //清空所有非叶节点的Add标记 Add[i]=0; } }
(2)点修改:
void Update(int L,int C){ for(int s=N+L;s;s>>=1){ Sum[s]+=C; } }
(3)点修改下的区间查询:
int Query(int L,int R){ int ANS=0; for(int s=N+L-1,t=N+R+1;s^t^1;s>>=1,t>>=1){ if(~s&1) ANS+=Sum[s^1]; if( t&1) ANS+=Sum[t^1]; } return ANS; }
(4)区间修改:
void Update(int L,int R,int C){ int s,t,Ln=0,Rn=0,x=1; //Ln: s一路走来已经包含了几个数 //Rn: t一路走来已经包含了几个数 //x: 本层每个节点包含几个数 for(s=N+L-1,t=N+R+1;s^t^1;s>>=1,t>>=1,x<<=1){ //更新Sum Sum[s]+=C*Ln; Sum[t]+=C*Rn; //处理Add if(~s&1) Add[s^1]+=C,Sum[s^1]+=C*x,Ln+=x; if( t&1) Add[t^1]+=C,Sum[t^1]+=C*x,Rn+=x; } //更新上层Sum for(;s;s>>=1,t>>=1){ Sum[s]+=C*Ln; Sum[t]+=C*Rn; } }
(5)区间修改下的区间查询:
int Query(int L,int R){ int s,t,Ln=0,Rn=0,x=1; int ANS=0; for(s=N+L-1,t=N+R+1;s^t^1;s>>=1,t>>=1,x<<=1){ //根据标记更新 if(Add[s]) ANS+=Add[s]*Ln; if(Add[t]) ANS+=Add[t]*Rn; //常规求和 if(~s&1) ANS+=Sum[s^1],Ln+=x; if( t&1) ANS+=Sum[t^1],Rn+=x; } //处理上层标记 for(;s;s>>=1,t>>=1){ ANS+=Add[s]*Ln; ANS+=Add[t]*Rn; } return ANS; }
以下为个人做题练手
hdu1754

#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <queue> #include <iomanip> #include <stack> #include <algorithm> #include <vector> #include <functional> using namespace std; typedef long long LL; #define FIL(Array, len, num) fill(Array, Array + len, num) #define lson l, m, rt << 1 #define rson m + 1, r, rt << 1 | 1 const double PI = 3.1415926; const double E = 2.1718281828; const int MAXN = 200005; const int INF = 0x3f3f3f3f; const int MOD = 1e9 + 7; inline int read() { int x = 0, f = 1;char ch = getchar(); while(ch < '0' || ch > '9'){if(ch == '-')f = -1;ch = getchar();} while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();} return x * f; } //推算都是由子叶开始推向根 //cnt 线段树下标 int n, cnt; int sum[MAXN << 2]; void Build() { cnt = 1; //根据原数组下标 + cnt = 存储下标 while(cnt < n + 2) cnt <<= 1; for(int i = 1;i <= n;++i) scanf("%d", &sum[cnt + i]); for(int i = cnt - 1;i > 0;--i) sum[i] = max(sum[i << 1], sum[i << 1 | 1]); } void Update(int L, int C) { sum[cnt + L] = C; for(int i = (cnt + L) >> 1;i > 0;i >>= 1) sum[i] = max(sum[i << 1], sum[i << 1 | 1]); } int Query(int L, int R) { int ret = 0; //想过把左右蓝色边界去掉,但是是不可行的 //例如取得区间是[3, 6],跟取区间[3, 4]的一样的结束条件 for(int l = cnt + L - 1, r = cnt + R + 1;l ^ r ^ 1;l >>= 1, r >>= 1) { if(~ l & 1) ret = max(ret, sum[l ^ 1]); if(r & 1) ret = max(ret, sum[r ^ 1]); } return ret; } int main() { int m; while(scanf("%d%d", &n, &m) != EOF) { Build(); while(m--) { char c[10]; int a, b; scanf("%s%d%d", &c, &a, &b); if(!strcmp(c, "Q")) printf("%d ", Query(a, b)); else Update(a, b); } } return 0; }
