做数据结构的课程设计顺便总结一下这四大算法,本人小白学生一枚,
如果总结的有什么错误,希望能够告知指正
普里姆算法如图所示prim
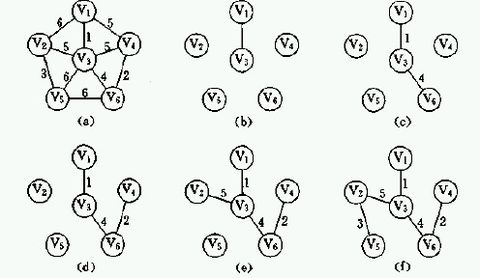
找出最短的边,再以这条边构成的整体去寻找与之相邻的边,直至连接所有顶点,生成最小生成树,时间复杂度为O(n2)
克鲁斯卡尔算法如图所示kruskal
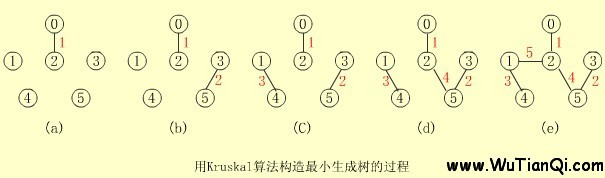
克鲁斯卡尔算法,假设连通网N=(N,{E}),则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V,{}),图中每个顶点
自成一个连通分量。在E中选择代价最小的边,若该边依附的定顶点落在T中不同的连通分量上,则将此边加入到T中,否则社区次边而选择
下一条代价最小的边。依次类推,直至T中所有的顶点都在同一连通分量上为止
迪杰斯特拉算法Dijkstra
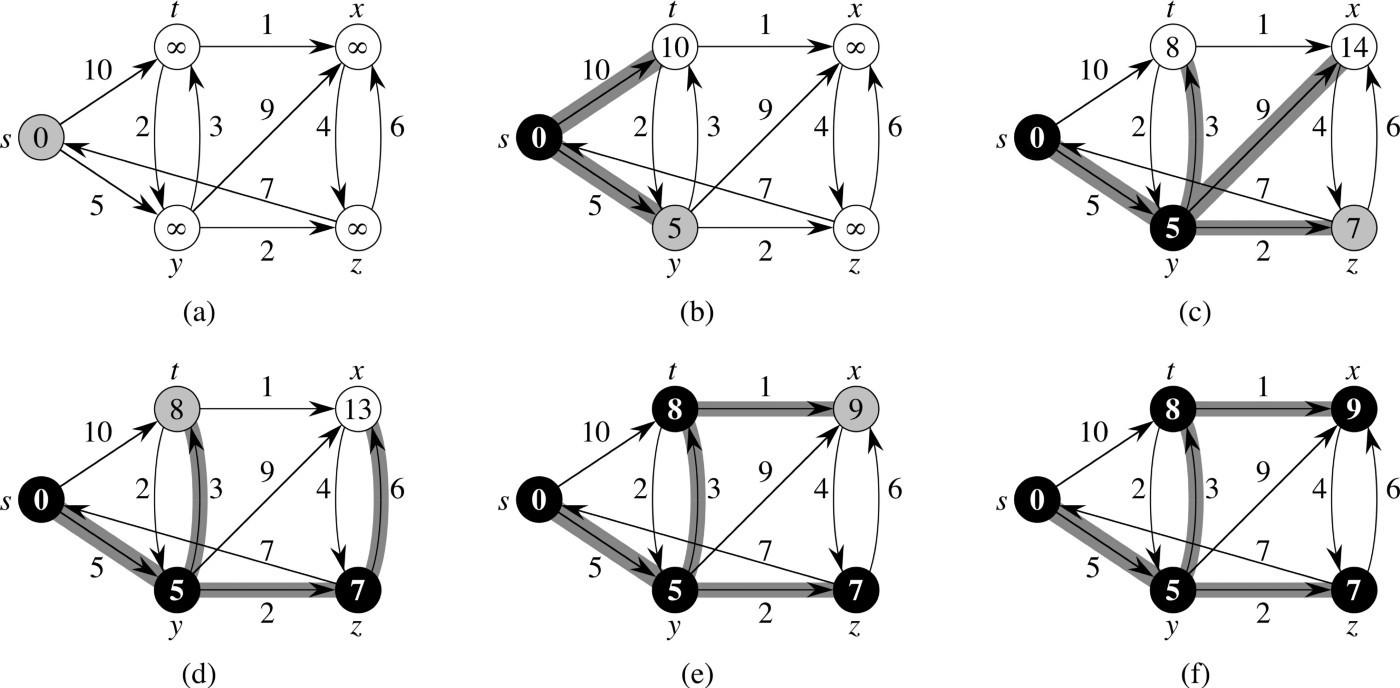

迪杰斯特拉算法和普里姆算法有相似的地方但是也有区别,都是贪心算法,但是普里姆算法的源点是任意的
而迪杰斯特拉算法的源点是特定的,他们都是把顶点分成两个集合
弗洛里德算法floyd
时间复杂度:O(n^3);
弗洛里德算法是求加权图中两个顶点之间的最短路路径,而迪杰斯特拉算法是求一个顶点到所有定点之间的距离
Floyd算法又称为弗洛伊德算法,插点法,是一种用于寻找给定的加权图中顶点间最短路径的算法。
算法过程:1,从任意一条单边路径开始。所有两点之间的距离是边的权,或者无穷大,如果两点之间没有边相连。
2,对于每一对顶点u和v,看看是否存在一个顶点w使得从u到w再到v比己知的路径更短。如果是更新它。
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
算法步骤如下:
1.初使时令S={V0},T={其余顶点},T中顶点对应的距离值
若存在,d(V0,Vi)为弧上的权值
若不存在,d(V0,Vi)为∝
2.从T中选取一个其距离值为最小的顶点W且不在S中,加入S
3.对T中顶点的距离值进行修改:若加进W作中间顶点,从V0到Vi的
距离值比不加W的路径要短,则修改此距离值
重复上述步骤2、3,直到S中包含所有顶点,即S=T为止