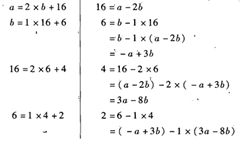1. 秦九昭算法:<多项式>
||
/
求n次多项式f(x)的值就转化为求n个一次多项式的值。
处理 :减ai后,除B,直到0为止
复数的模 |Z|=|a+bi|=sqrt(a*a+b*b) , 除法 (a+bi)/(c+di)=(ac+bd)/(c*c+d*d)+(bc-ad)/(c*c+d*d) (分子分母同乘(c-di))
2. 差分 <多项式>
前向差分
函数的前向差分通常简称为函数的差分。对于函数![]() ,如果在等距节点:
,如果在等距节点:
在微积分学中的有限差分(finite differences),前向差分通常是微分在离散的函数中的等效运算。差分方程的解法也与微分方程的解法相似。当![]() 是多项式时,前向差分为Delta算子(称
是多项式时,前向差分为Delta算子(称![]() 为差分算子[2]),一种线性算子。前向差分会将多项式阶数降低 1。
为差分算子[2]),一种线性算子。前向差分会将多项式阶数降低 1。
逆向差分
一阶差分的差分为二阶差分,二阶差分的差分为三阶差分,其余类推。记:
![]() 为
为![]() 的
的![]() 阶差分。] -------[From Wikipedia]
阶差分。] -------[From Wikipedia]
处理:计算xi相邻两项差 得序列x2i,计算x2i相邻两项差 得序列x3i,重复以上过程,直到xni的各项值相等。再回算。
3. 抽屉原理
任何一个自然数都可分解质因数。N!=1*2*3*4*5*6*...*N=2^a*3^b*5^c*7^d......=(2*5)^c*2^(a-c)*3^b*7^d......=10^c*2^(a- c)*3^b*7^d....
在分解质因数时小的质数的幂次一定不小于大的质数的幂次大,所以a>=c。求 N! (1*2*3*4*5*...*N)里有多少个5其实可以转化成:
N!中:是5的倍数的数+是5^2的倍数的数+5^3.....
如50!:
含有10个5的倍数的数:5,15,20,25,30,35,40,45,50 【50/5=10】
含有2个5^2的倍数的数:25,50【50/(5^2)=2】
可见N!中一共有12个5相乘,那么尾0也必有12个
4. i^2%m
n:1~![]() 循环结m (5: 1 4 4 1 0 6: 1 4 3 4 1 0 7: 1 4 2 2 4 1 0 21: 1 4 9 16 4 15 7 1 18 16 16 18 1 7 15 4 16 9 4 1 0)
循环结m (5: 1 4 4 1 0 6: 1 4 3 4 1 0 7: 1 4 2 2 4 1 0 21: 1 4 9 16 4 15 7 1 18 16 16 18 1 7 15 4 16 9 4 1 0)
对称:m/2
推广:i^x%m 循环结都是m,若x为偶数,关于m/2对称
处理: 如果 a[1%n] != a[2%n],那么 a[2%n] != a[4%n],那么 a[1%n] == a[4%n];
如果 a[1%n] == a[2%n],那么 a[2%n] == a[4%n],那么 a[1%n] == a[4%n]。
所以 a[1%n] == a[4%n]
同样的方法得到:
a[1%n] == a[9%n],
a[1%n] == a[16%n],
所有下标是 i 平方 mod n 都相等,下标不是 i 平方 mod n 都相等。
5. 扩展欧几里得 <二元一次方程>
int x=1,y=0,xx=0,yy=1; int gcd(int a,int b) { if(b==0) return a; int tx,ty; tx=x,ty=y; x=xx,y=yy; xx=tx-(a/b)*xx,yy=ty-(a/b)*yy; gcd(b,a%b); } //改良版:ax+by=bx’+(a-a/b)y’ int gcd(int a,int b) { int t,d; if(b==0) { x=1,y=0; return a; } d=gcd(b,a%b); t=x, x=y, y=t-(a/b)*y; return d; }
推论:线性丢番图方程(二元一次方程)ax+by=c有解 ![]() gcd(a,b)|c 否则无解;
gcd(a,b)|c 否则无解;
解为:x=x0+(b/d)*k , y=y0-(a/d)*k (d=gcd(a,b))
6. 逆元
1. 扩展欧几里得解法:
前提:gcd(a,m)=1;
处理:a*x![]() 1(mod m)
1(mod m) ![]() a*x+m*y=1; 扩展欧几里得解得x0;
a*x+m*y=1; 扩展欧几里得解得x0;
x=x0+k*m/gcd(a,m) ![]() 逆元结果:x=x0>0?(x0%m):(x0%m+m);
逆元结果:x=x0>0?(x0%m):(x0%m+m);
2. 费马小定理解法:
前提:gcd(a,m)=1; m为素数;
处理:
7. 素因子分解系列
n = p1 ^ e1 * p2 ^ e2 *..........*pn ^ en
大素数判断和素因子分解(miller-rabin,Pollard_rho算法)
1. 素因子个数
sum ( n)= ( 1 + e1 ) * ( 1 +e2 ) * ...* ( 1 +en );
sum (n * n) = (1+2*e1)*(1+2*e2)*...*(1+2*en) ;
2. 因子和
Sum=(p1^0+p1^1….p1^e1)*(p2^0+p2^1…p2^e2)……(pn^0+…pn^en);
因子和 s是积性函数,即 :gcd(a,b)=1==> s(a*b)= s(a)*s(b)
3.欧拉函数 (小于等于n的,与n互质的数的个数)
![]() (mn)=
(mn)=![]() (n)*
(n)*![]() (m)只在gcd(n,m)=1时成立(积性)
(m)只在gcd(n,m)=1时成立(积性)
8. 素数筛选
bool prime[N]; void is_prime() { memset(prime,0,sizeof(prime)); for(int i=2;i<N;i++) { if(!prime[i]) { for(int j=i+i;j<N;j+=i) prime[j]=1; } } }