题意：

线段树求面积并

分析：

看了几个博客+自己画画图+看代码，试着理解了扫描线，有一些感受，但是还是没能掌握。
推荐几个博客，觉得讲的还是比较好的。

我就简单记录一下我现在的一些体会。

有一个很重要的概念就是投影，

分析:

1.矩形比较多，坐标也很大，所以横坐标需要离散化（纵坐标不需要），熟悉离散化后这个步骤不难，所以这里不详细讲解了，不明白的还请百度

2.重点：扫描线法：假想有一条扫描线，从左往右（从右往左），或者从下往上（从上往下）扫描过整个多边形（或者说畸形。。多个矩形叠加后的那个图形）。如果是竖直方向上扫描，则是离散化横坐标，如果是水平方向上扫描，则是离散化纵坐标。下面的分析都是离散化横坐标的，并且从下往上扫描的。

扫描之前还需要做一个工作，就是保存好所有矩形的上下边，并且按照它们所处的高度进行排序，另外如果是上边我们给他一个值-1，下边给他一个值1，我们用一个结构体来保存所有的上下边

struct segment
{
double l,r,h;   //l，r表示这条上下边的左右坐标，h是这条边所处的高度
int f;   //所赋的值，1或-1
}

接着扫描线从下往上扫描，每遇到一条上下边就停下来，将这条线段投影到总区间上（总区间就是整个多边形横跨的长度），这个投影对应的其实是个插入和删除线段操作。还记得给他们赋的值1或-1吗，下边是1，扫描到下边的话相当于往总区间插入一条线段，上边-1，扫描到上边相当于在总区间删除一条线段（如果说插入删除比较抽象，那么就直白说，扫描到下边，投影到总区间，对应的那一段的值都要增1，扫描到上边对应的那一段的值都要减1，如果总区间某一段的值为0，说明其实没有线段覆盖到它，为正数则有，那会不会为负数呢？是不可能的，可以自己思考一下）。

每扫描到一条上下边后并投影到总区间后，就判断总区间现在被覆盖的总长度，然后用下一条边的高度减去当前这条边的高度，乘上总区间被覆盖的长度，就能得到一块面积，并依此做下去，就能得到最后的面积

（这个过程其实一点都不难，只是看文字较难体会，建议纸上画图，一画即可明白，下面献上一图希望有帮组）

引用一下一个图片

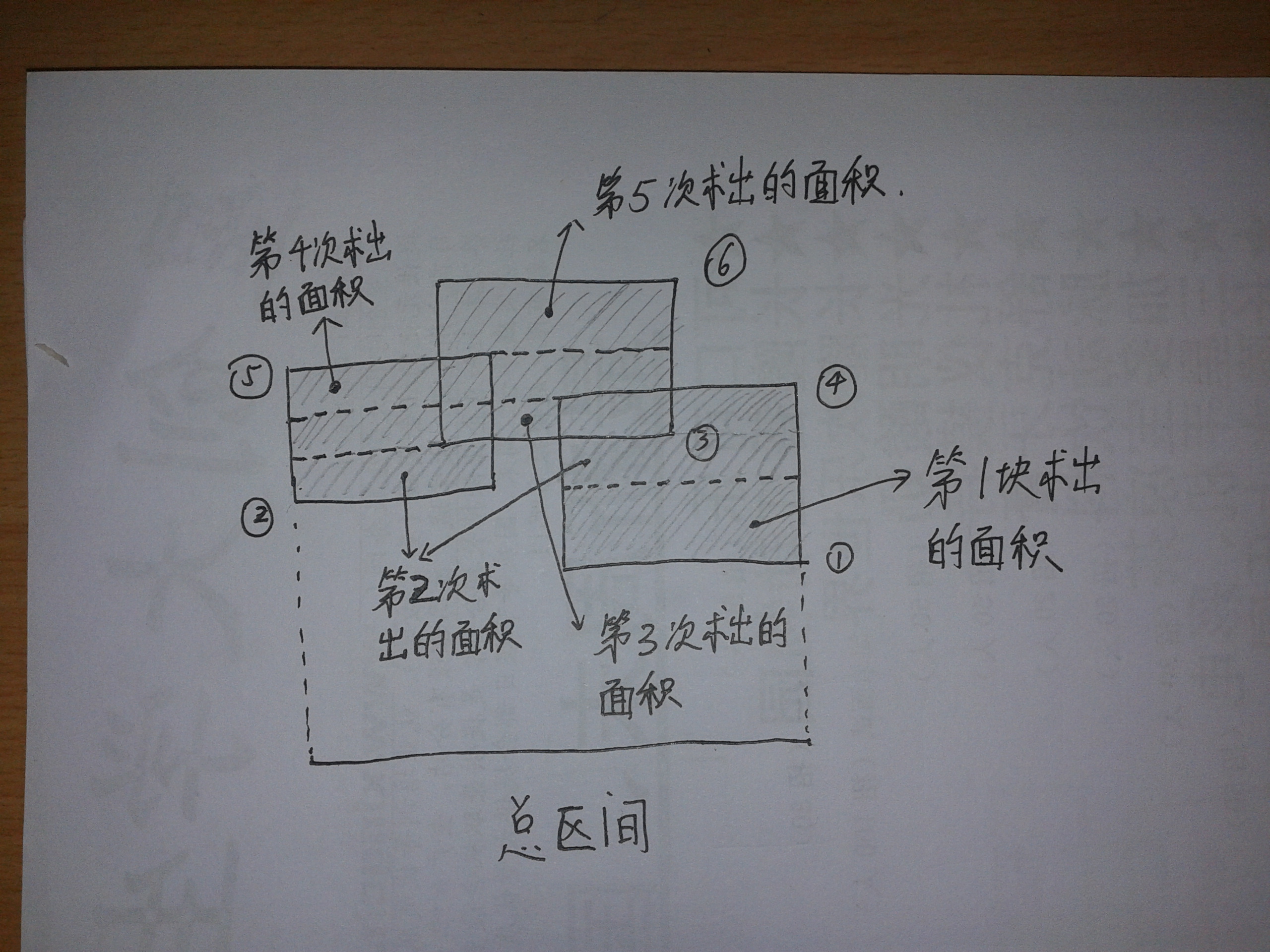
Online AC Code

#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1

const int maxn = 2222;
int cnt[maxn << 2];		//对于rt，若cnt[rt]>0，则对应子树的线段区间被完全覆盖；若cnt[rt]==0，则被部分覆盖/完全没有覆盖
double sum[maxn << 2];	//对于rt,sum[rt]为对应子树覆盖的到线段区间的长度
double X[maxn];			//所有矩形的左右边界“直线”（每个矩形有两条这种直线，分别占用本数组的两个元素）

//（矩形）上/下边界“线段”
struct Seg {
	double h , l , r;	//h高度, l左端点, r右端点
	int s;	//s==1为下边界线段； s==-1为上边界线段
	Seg(){}
	Seg(double a,double b,double c,int d) : l(a) , r(b) , h(c) , s(d) {}

	//需要按照上/下边界线段的高度来排序
	bool operator < (const Seg &cmp) const {//看运算符重载???
		return h < cmp.h;
	}
}ss[maxn];

void PushUp(int rt,int l,int r) {
	if (cnt[rt]) sum[rt] = X[r+1] - X[l];		//子树rt的线段区间完全覆盖			
	else sum[rt] = sum[rt<<1] + sum[rt<<1|1];	//子树rt的线段区间没有完全覆盖（没有覆盖/部分覆盖）
}

//需要插入/移出线段树的“上/下边界线段”： 左端点X[L], 右端点X[R+1], c==1下边界/c==-1上边界
//待插入/移除的线段树子树范围
void update(int L,int R,int c,int l,int r,int rt) {
	if (L <= l && r <= R) {
		cnt[rt] += c;
		PushUp(rt , l , r);
		return ;
	}

	int m = (l + r) >> 1;
	if (L <= m) update(L , R , c , lson);
	if (m < R) update(L , R , c , rson);

	PushUp(rt , l , r);
}
//二分
int Bin(double key,int n,double X[]) {
	int l = 0 , r = n - 1;
	while (l <= r) {
		int m = (l + r) >> 1;
		//1. 第1个分支是“递归终止条件”
		if (X[m] == key) return m;
		//2. 第2、3个分支是“二分后的两个子问题”
		if (X[m] < key) l = m + 1;
		else r = m - 1;
	}
	return -1;
}

int main() {
	int n , cas = 1;
	while (~scanf("%d",&n) && n) {
		int m = 0;
		while (n --) {
			double a , b , c , d;
			scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
			X[m] = a;
			ss[m++] = Seg(a , c , b , 1);
			X[m] = c;
			ss[m++] = Seg(a , c , d , -1);
		}
		sort(X , X + m);
		sort(ss , ss + m);

		//X[]已经递增排序后，如下操作使得X[]中不等的数字依次放在靠前
		//例如X[]={1,2,2,5,5,7} --> X[]={1,2,5,7,5,7}
		//处理后，其中X[0, ... ,k-1]为不等的数字
		int k = 1;
		for (int i = 1 ; i < m ; i ++) {
			if (X[i] != X[i-1]) X[k++] = X[i];
		}

		memset(cnt , 0 , sizeof(cnt));
		memset(sum , 0 , sizeof(sum));

		//下面为m-1轮扫描的过程
		double ret = 0;
		for (int i = 0 ; i < m - 1 ; i ++) { //i=0-->m-2
			int l = Bin(ss[i].l , k , X);
			int r = Bin(ss[i].r , k , X) - 1;

			//printf("L: %d  R： %d
",l,r);
			//“上/下边界线段”长度不为0时，采取更新线段树。否则，这种“上/下边界线段”横向收缩为一个点
			if (l <= r) update(l , r , ss[i].s , 0 , k - 1, 1);

			//每轮扫描：更新线段树后，累计本轮扫描新增的面积大小
			ret += sum[1] * (ss[i+1].h - ss[i].h);
		}
		printf("Test case #%d
Total explored area: %.2lf

",cas++ , ret);
	}
	return 0;
}