原文:http://users.rowan.edu/~polikar/WTpart3.html
译文:https://blog.csdn.net/alihouzi/article/details/45190489
小波级数:CWT的离散化
连续小波函数为:
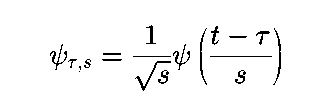
式 3.22
将s = s_0^j,tau = k*s_0^j*tau_0代入上式,则小波函数变为:
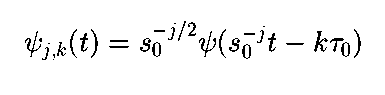
式 3.23
如果{psi_(j,k)}为一组正交基,则小波级数变换变为:
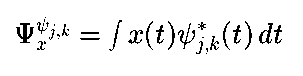
式 3.24
或者
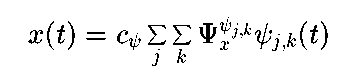
式 3.25
小波级数需要{psi_(j,k)}满足正交,或者双正交,或者框架条件。如果{psi_(j,k)}不是归一化正交,则式3.24变为:
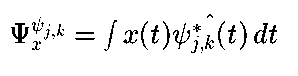
式 3.26
其中hat{ psi_{j,k}^*(t)}为二重双正交或者二重框架(此处*表示共轭)。
如果{psi_(j,k) }为正交或者双正交,上述变换为非冗余的。如果{psi_(j,k) }为框架,则变换是冗余的。当然,从另外一方面讲,构造框架比发现正交或者双正交基要容易得多。
下面的类比可能会帮助更清晰地理解上述概念。将整个处理过程当作观察一个具体的物体,人眼首先是粗略地对物体进行观察,其程度与眼睛距物体的远近而有所不同。这对应着调整尺度参数s_0^(-j)。如果是近距离详细观察物体,j为负,并且绝对值很大(低尺度,高频率,对信号进行详细分析)。以很小的幅度缓慢地移动眼睛,对应着很小的tau = k*s_0^j*tau_0。如果j为负数并且绝对值很大时,tau则对应着时间上的微小变化(高采样频率),而s_0^-j则变化很大(低尺度,高频率,采样频率很高)。尺度参数也可以看作是放大。
采样频率到底最低到多少仍然能保证信号的完全重构?这是对上述过程进行最优化时必须回答的主要问题。从编程的角度来说,最方便的数值是 s_0=2,tau=1。显然,当采样频率尽可能低的时候,可能的正交小波数目也自然减少了。
前面给出的连续小波变换的例子实际上就是给定信号的小波级数。其参数的选择与信号有关。由于并不需要信号的重构,采样频率有时候远偏离于标准值。在不同的例子中,s_0的取值范围从2到10,tau_0的范围从2到8。
在结束小波级数讨论的时候,还有一个问题需要讨论。虽然离散化的小波变换,即小波级数可以利用计算机来运算,但运算时间从数秒到数小时不等。这主要依赖于信号的长度及所需的分辨率。计算信号的小波变换还有一种令人着迷的快速算法,即离散小波变换(DWT)。关于DWT的内容稍后介绍。