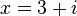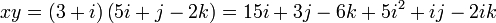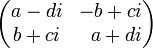四元数
四元数是由爱尔兰数学家威廉·卢云·哈密顿在1843年发现的数学概念。四元数的乘法不符合交换律。
明确地说，四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话，四元数就代表着一个四维空间，相对于复数为二维空间。
定义
复数是由实数加上元素 i 组成，其中
。
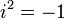相似地，四元数都是由实数加上三个元素 i、j、k 组成，而且它们有如下的关系：
每个四元数都是 1、i、j 和 k 的线性组合，即是四元数一般可表示为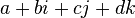
。
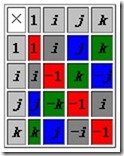
要把两个四元数相加只需将相类的系数加起来就可以，就像复数一样。至于乘法则可遵循以下的乘数表：
例子
假设：
那么：
性质
四元数不像实数或复数那样，它的乘法是不可交换的，例如
；
；
。
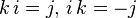四元数是除法环的一个例子。除了没有乘法的交换律外，除法环与域是相类的。特别地，乘法的结合律仍旧存在、非零元素仍有唯一的逆元素。
四元数形成一个在实数上的四维结合代数（事实上是除法代数），并包括复数，但不与复数组成结合代数。 四元数（以及实数和复数）都只是有限维的实数结合除法代数。
四元数的不可交换性往往导致一些令人意外的结果，例如四元数的 n-阶多项式能有多于 n 个不同的根。 例如方程式 
就有无数多个解。 只要是符合 
的实数，那么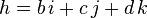 
就是一个解。
一个四元数 
的共轭值定义为：
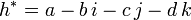
而它的绝对值则是非负实数，定义为：
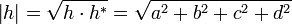
注意
，一般状况下不等于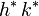
。
四元数的乘逆可以
算得。
以矩阵表示四元数
有两种方法能以矩阵表示四元数，并以矩阵之加法、乘法应用于四元数之加法、乘法。
第一种是以二阶复数矩阵表示。若 h = a + bi + cj + dk 则它的复数形式为：
这种表示法有如下优点：
- 所有复数 (c = d = 0) 就相应于一个实矩阵。
- 四元数的绝对值的平方就等于矩阵的行列式。
- 四元数的共轭值就等于矩阵的共轭转置。
- 对于单位四元数 (|h| = 1) 而言，这种表示方式给了四维球体和SU(2)之间的一个同型，而后者对于量子力学中的自旋的研究十分重要。
第二种则是以四阶实数矩阵表示：
其中四元数的共轭等于矩阵的转置。