题面
因为有一点忘了算法,然后想借助题来复习一下,所以有一些算法会复习的比较详细。
首先可以看到,这是一个先以(1)为根建一颗最大生成树,再用倍增求(LCA)。
并查集
具体来说现将一个集合的中所有元素进行个体分离,然后根据关系进行集合,最后判断几个点是否有关系只需判断是否在一个集合中即可。
int find(int t)
{
if(f[t]==t)
{
return t;
}
else
{
return f[t]=find(f[t]);
}
}
最大生成树
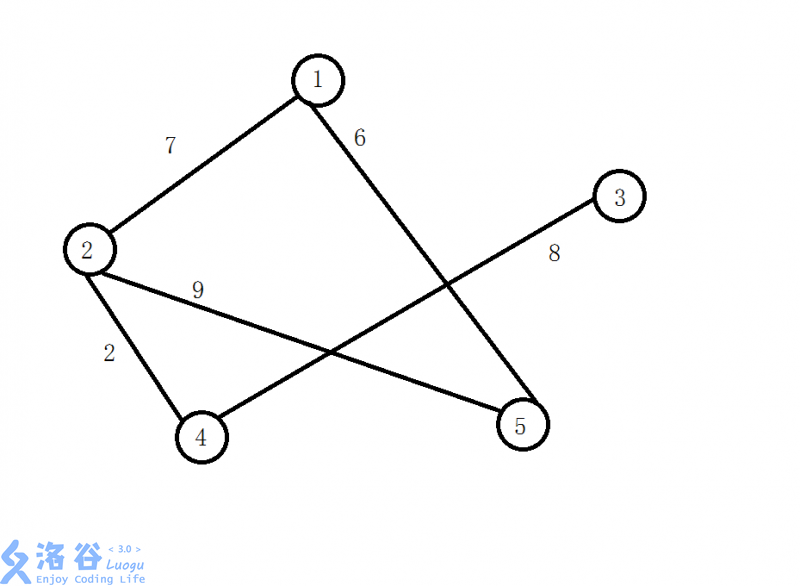
我们将对边权进行排序,边权大的将被优先选择。选边时,若这一条边的两个顶点不在一个集合内就将二者合并,这里就用到了并查集的思想,并将加入的边的条数增加(1),然后建边,当已经选了(n-1)条边时就跳出循环,因为(n)个点需要(n-1)条边才能够两两互达且为树。
下面就是该图的最大生成树:
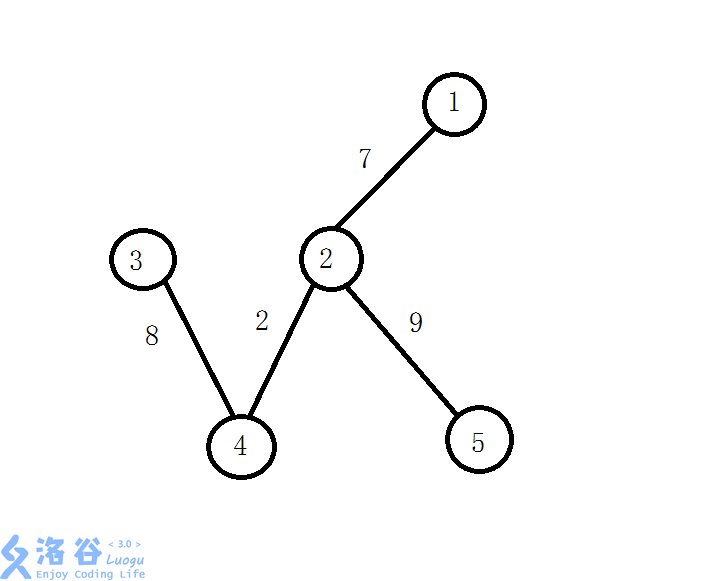
倍增
1号点第(i)次跳跃跳到的格子为(1+2^i)。那么如果我们设(g[x][i])表示的是(x)号点跳第(i)次的位置的话,那么(g[x][i]=g[g[x][i−1]][i−1]),此处感觉十分的好理解。显然,我们可以先从(x)点跳到离(y)点最近的且不超过(y)点的那个点。然后再从该点起步,继续跳下去,直到跳到(y)点为止。这种算法的时间复杂度为(O(nlog2n))。
LCA
最近一直在刷LCA的题,然后就不在这里展开讲了。
int lca(int x,int y)
{
int ans=inf;
if(deep[x]<deep[y])
{
int t=x;
x=y;
y=t;
}
for(int i=20;i>=0;i--)
{
if(deep[p[x][i]]>=deep[y])
{
ans=min(ans,w[x][i]);
x=p[x][i];
}
}
if(x==y)
{
return ans;
}
for(int i=20;i>=0;i--)
{
if(p[x][i]!=p[y][i])
{
ans=min(ans,min(w[x][i],w[y][i]));
x=p[x][i];
y=p[y][i];
}
}
ans=min(ans,min(w[x][0],w[y][0]));
return ans;
}
注意了,当有(2)棵树或多棵树时,要将没有深度的点(即不与点(1)在同一棵树内的点)的深度改为(1),如果不改的话就会输出(0)哦。
下面我将把代码中的一些重要的部分拆开来解释,方便大家理解。
代码段还请见(lca())部分。
因为我们规定了是(x)去找(y),所以当(y)比(x)深时就要交换(x)和(y)。调换(x)和(y)并不会影响答案,因为(lca(x,y)=lca(y,x))。
if(deep[x]<deep[y])
{
int t=x;
x=y;
y=t;
}
这里是让(x)和跳到和(y)同一层,并在路上记录最小值, 若(y)就是(x)的公共祖先(见下图)就直接返回答案即可。否则就让(x)和(y)一起跳到它们的最近公共祖先的前一步的那个点去,最后再跳一步(即跳到(x)和(y)的最近公共祖先那里去)。最后再返回所经过的路径中的最小值即可。注意赋值的顺序不要反了。
for(int i=20;i>=0;i--)
{
if(deep[p[x][i]]>=deep[y])
{
ans=min(ans,w[x][i]);
x=p[x][i];
}
}
if(x==y)
{
return ans;
}
for(int i=20;i>=0;i--)
{
if(p[x][i]!=p[y][i])
{
ans=min(ans,min(w[x][i],w[y][i]));
x=p[x][i];
y=p[y][i];
}
}
ans=min(ans,min(w[x][0],w[y][0]));
return ans;