problem0

2、基本形式:令a[l~r]/b[l~r]=x
3、二分关键:二分x,通过二分过程中的a[l~r]/b[l~r]与m比较](m是二分x时的mid) ,根据x的二分结果调正分子分母大小。
4、令c[i]=a[i]-m*b[i
则问题转化成 有没有c[l~r]>=0
等价于判断c中有没有大于等于0的数(只要有一个就可以了,有一个的时候子区间就那一位)
5、注意事项,所有变量几乎都是double类型,所以没有类似于整形的终止条件,故直接二分50次即可达到既定精度。

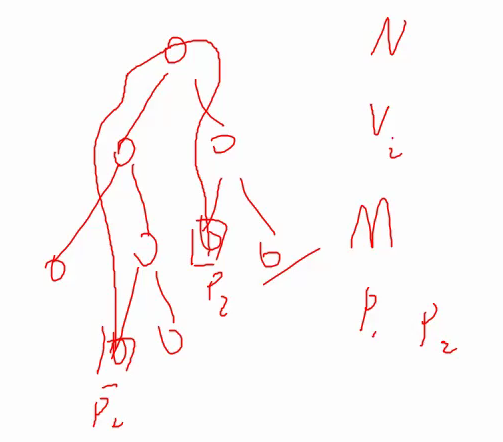
题目:n个点(用n-1条边)组成一棵树,每个点有一个权值vi,现在有m条询问,每条询问给两个点p1,p2,两点之间会有一条路径相连接(事实证明在树中是只有一条的)。询问内容是路径p1到p2上的所有点权,能否组出至少一个三元组(a,b,c),使以a,b,c为边长能形成一个三角形。(对于每个询问,输出yes或no)
范围:1<=n,m<=100000 1<=vi<2^31 1<=p1,p2<=100000
这道题就相当于把路径上的点从小到大与斐波那契数列相对照。设a<=b<=c,由常识可知a+b>c时,三遍才能组成三角形。由于只要有一组a,b,c满足条件就输出yes,那我们直接看看什么情况下才输出no(因为情况少)。当路径上的点从小到大排序后,从第三项起每项大于等于斐波那契数列对应项的时候(1,1,2,3,5,8...),这些边就刚好组不成三角形。最坏情况下,就是刚好等于斐波那契数列。而斐波那契数列大约在第46项的时候就超过int最大值(2^31),而点权都是int范围的,因此当路径上有超过45个点的时候,第46大的数肯定小于int最大值(2^31),达不到斐波那契数列的第46项,而这样的话第46大的数就一定小于第44大的数加第45大的数(假设前45个数为斐波那契数列),那么将至少有三条边就能组成一个三角形。因此路径上点数>45时直接输出yes,否则暴力一下(暴力方法:把路径上的所有点权取出来排序,从小到大判断连续3个数是否能组成三角形即可),毕竟 100000*(45*log(45)+45)≈100000*(45*6+45)=100000*45*7=31500000 的时间复杂度还是能接受的。(用sort排序的话时间复杂度最大是是45*log(45))
另外两个结点的最短距离(也就是两节点最短路径之间的节点数量)需要通过两点LCA求得。这里建议倍增。