我是一个小沙比,爆零本领强~
T1
看起来是一道很捞的、做过无数遍的区间最大值。
直接$O(n^3)$做一做就完了……
具体做法就是预处理每行的前缀和,然后二重循环枚举一个固定的列区间,再用单调队列的思想,从第一行不停向下扩展行区间,如果矩阵内总和$gt k$ 了就从行区间顶部不停删行,删到矩阵内总和$le k$ 为止。每当矩阵总和满足限制时,更新矩阵面积最大值即可。
当然如果你很想大战$T1$的话,可以写个$O(n^2*log(n^2))$的主席树?

1 #include<cmath> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<iostream> 6 #include<algorithm> 7 #define N 501 8 using namespace std; 9 inline int read(){ 10 int x=0; bool f=1; char c=getchar(); 11 for(;!isdigit(c);c=getchar()) if(c=='-') f=0; 12 for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^'0'); 13 if(f) return x; 14 return 0-x; 15 } 16 int n,m,e[N][N],sum[N][N],x,ans; 17 int main(){ 18 n=read()+1,m=read(); 19 int i,j,k,go; 20 for(i=1;i^n;++i) 21 for(j=1;j^n;++j) 22 sum[i][j]=sum[i][j-1]+read(); 23 for(i=1;i^n;++i){ 24 for(j=i;j^n;++j){ 25 x=0, go=1; 26 for(k=1;k^n;++k){ 27 x+=sum[k][j]-sum[k][i-1]; 28 while(x>m) x-=sum[go][j]-sum[go][i-1], ++go; 29 ans=max(ans,(j-i+1)*(k-go+1)); 30 } 31 } 32 } 33 printf("%d ",ans); 34 return 0; 35 }
T2
这是一道考验水平的$dp$题(机房最高分$70$)
0~30pts:
你写的开心就好
40~50pts:
不知道
60~90pts:
由于是一条链,且对于相邻的两个机场之间的点,我们可以用二分等方法快速求出每个点补给来源(就是离它最近的一个机场)的分界处。所以可以考虑链上$dp$。
设$f(i)$表示把最后一个机场设在第 $i$ 个城市时,前 $i$ 个点都得到补给所需的总代价的最小值。
易推$f(i)=min{f(j-1)+sum_{k=j}^{i}min(d_k-d_j,d_i-d_k)}+cost_i space | space (j<i,j≠0)$
其实就是枚举上一个机场的位置,然后计算中间这些点到最近机场的距离代价。
前面说过,相邻两个机场之间的点,一定会分成左右两部分计算,左边部分离左边的机场更近,右边部分离右边的机场更近。只要找到这个分界处,区间距离总和随意预处理就好了(二维前缀和?)。
找到分界处有两种方法,一种是直接二分位置($O(log(n))$),一种是根据分界处的单调变化性(左边的机场 $j$ 向一个方向移动,分界处也只会向这个方向移动)单调修改($O(n)$)。
当然有可能前面没设过机场$(j=0)$,这时转移是$f(i)=cost_i+sum_{k=1}^{i}(d_i-d_k)$。
100pts:
这个dp有点新式……
设$f(i,j)$表示当前最后一个机场设在了节点 $j$ 时(建立顺序任意),以 $i$ 号节点为根的子树中所有点都得到补给所需的总代价的最小值,$g(i)=min{f(i,j)}$。(王爷定义的 $j$ 跟我定义的不太一样,我看了代码之后感觉应该这样定义)
然后转移是这样的
$f(i,j)=sum_{v∈son_i}min(f(v,j)-cost_j,g(v))+dist(i,j)+cost_j$
其中$dist(i,j)$表示$i$与$j$在树上的距离,这个可以$O(n^2)$预处理。
转移就这么些道理:
首先我们要累加当前点得到补给的代价 以及在$j$建机场的代价,也就是 $dist(i,j)+cost_j$。
$f(v,j)-cost_j$ 表示沿用离$v$最近的机场$j$,$-cost_j$是因为建这个机场的代价已经在$f(v,j)$的转移中累加过了(因为离$v$最近的机场也是$j$),为了避免重复花费建机场的代价,我们减去它,之后再重新加上即可。
$g(v)$ 表示在 $v$ 新建一个机场,这样就可以取 $min{f(v,x)} space | space x为任意节点}$,因为跟上一个建的机场没关系了。
但这时候有个问题:新建的机场不一定离点$i$最近啊!为什么可以直接累加点$i$到最新建的机场的距离为点$i$得到补给的代价呢?
这个得有一些$dp$经验才明白,其实是因为按照我们的转移方法,所有建立机场的顺序都被考虑过,而我们取的是总代价的最小值。
再细讲,举个例子:对于机场建设完全相同,但建设顺序不同的情况(假设图中根在上方)
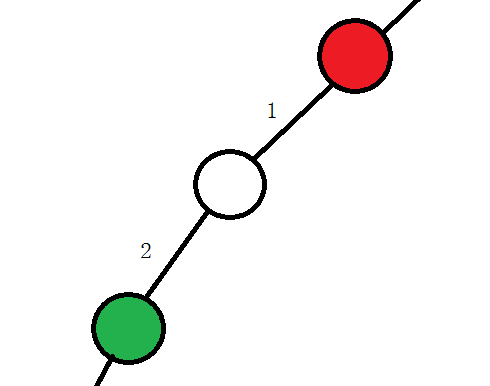
如果我们先在红点建机场,再在绿点设机场,因为绿点是白点儿子,所以对于$f(白点,绿点)$,白点的代价可能被算为到绿点的距离 $2$,但实际上它离红点更近,代价应该是到红点的距离 $1$。
但反过来想,我们既然能够考虑所有情况,那肯定包含红绿两点交换建机场的顺序的情况,比如说,我们就可以把$f(绿点,绿点)$更新给$f(白点,红点)$,这时白点的代价就计算为白点到红点的距离 $1$ 了。
以后再合并答案的时候,由于上述两种顺序的总代价只在计算白点代价时有差异,而我们求的是代价的最小值,于是错误的计算就被更新掉了(因为错误的情况计算白点的代价更大)。
最后的答案即为$g(root)$。

1 #include<cstdio> 2 #include<cstring> 3 #include<cctype> 4 #include<cmath> 5 #include<algorithm> 6 #define rep(i,s,t) for(int i=s;i<=t;i++) 7 #define dwn(i,s,t) for(int i=s;i>=t;i--) 8 using namespace std; 9 inline int read() { 10 int x=0,f=1;char c=getchar(); 11 for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; 12 for(;isdigit(c);c=getchar()) x=x*10+c-'0'; 13 return x*f; 14 } 15 typedef long long ll; 16 const int maxn=2610; 17 int n,cost[maxn],first[maxn],nxt[maxn<<1],to[maxn<<1],dis[maxn<<1],e; 18 void AddEdge(int u,int v,int w) { 19 to[++e]=v;dis[e]=w;nxt[e]=first[u];first[u]=e; 20 to[++e]=u;dis[e]=w;nxt[e]=first[v];first[v]=e; 21 } 22 int dist[maxn][maxn]; 23 void dfs(int x,int fa,int s) { 24 for(int i=first[x];i;i=nxt[i]) if(to[i]!=fa) dist[s][to[i]]=dist[s][x]+dis[i],dfs(to[i],x,s); 25 } 26 int f[maxn][maxn],g[maxn]; 27 void dp(int x,int fa) { 28 for(int i=first[x];i;i=nxt[i]) if(to[i]!=fa) dp(to[i],x); 29 rep(j,1,n) { 30 f[x][j]=cost[j]+dist[x][j]; 31 for(int i=first[x];i;i=nxt[i]) if(to[i]!=fa)f[x][j]+=min(g[to[i]],f[to[i]][j]-cost[j]); 32 } 33 g[x]=f[x][1]; 34 rep(i,2,n) g[x]=min(g[x],f[x][i]); 35 } 36 int main() { 37 //freopen("design.in","r",stdin); 38 //freopen("design.out","w",stdout); 39 n=read(); 40 rep(i,1,n) cost[i]=read(); 41 rep(i,1,n-1) { 42 int u=read(),v=read(),w=read(); 43 AddEdge(u,v,w); 44 } 45 rep(i,1,n) dfs(i,0,i); 46 dp(1,0); 47 printf("%d ",g[1]); 48 return 0; 49 }
T3
这题引出了“线段树优化建图”这个东西?我可能没写过呢。
其实很好理解,就是对于区间向区间连边的题目(而不是点向点连边),可以维护一棵线段树,线段树的每个节点存的是一段点区间,并向它的左右儿子都连一条权值为$0$的边。这样就可以在$log$级别的复杂度内从区间向区间连边。
这题更简单了,只是点向区间连边……又因为每个点只向一个它能到达的区间连一次边,我们甚至不用再建图连边,直接操作一个点能到达的的区间即可。我的$code$就没建图。
当然,我们要预处理出每个点能到达的区间。
然后我们怎么搞区间连边的单源最短路?$spfa$?
$spfa$有一个缺点,就是不能确定每个点的$dis$(到起点的最短路长度)什么时候会成为最小值(当然了,一个点被更新$总点数-1$次后肯定是最小值,但对所有点都这样判的话就被卡成暴力了),也就是$dis$值一定不会再发生变化。而我们只能用线段树快速完成区间更新$dis$值,并不知道哪些点的$dis$值发生了变化,我们只能暴力把这些点放入队列,这样时间复杂度就向暴力退化了。
那我们怎么快速求最短路?只能$dijkstra$咯,要知道这是一个很优秀的算法(带负权边除外)。这题没有负权边,所以可以用它。
于是我们只需要在线段树上维护一下区间$dis$的最小值,每次随便查询一个$dis$值最小的位置,记录它的答案为$dis$值,然后以它为起点更新它能到达的区间的$dis$值即可。用完这个点后,为了避免以后查询$dis$值最小的点再查到它,我们要把这个点从线段树上删除(删除的方法随意,我直接把这个点的$dis$值赋回$inf$ 并打上一个删除标记)。

1 #include<bits/stdc++.h> 2 #define ll long long 3 #define N 152505 4 const ll inf=1ll<<62; 5 using namespace std; 6 inline int read(){ 7 int x=0; bool f=1; char c=getchar(); 8 for(;!isdigit(c);c=getchar()) if(c=='-') f=0; 9 for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^'0'); 10 if(f) return x; 11 return 0-x; 12 } 13 int n,s,t,x[N],y[N],z[N],l[N],r[N]; 14 int root,L,R,u; ll Dis; 15 struct SegTree{ 16 struct T{ 17 int son[2]; 18 ll dis,tag; //min,max 19 bool del; 20 }tr[N<<3]; 21 int cnt; 22 inline void pushup(int o){ 23 tr[o].dis = min(tr[tr[o].son[0]].dis, tr[tr[o].son[1]].dis); 24 //printf("pushup:%lld %lld ",tr[tr[o].son[0]].dis, tr[tr[o].son[1]].dis); 25 } 26 inline void pushdel(int o){ 27 tr[o].del = tr[tr[o].son[0]].del & tr[tr[o].son[1]].del; 28 } 29 void build(int &o,int l,int r){ 30 o=++cnt; 31 tr[o].tag=inf, tr[o].del=0; 32 if(l==r){tr[o].dis=inf; tr[o].son[0]=tr[o].son[1]=0; return;} 33 int mid=(l+r)>>1; 34 build(tr[o].son[0],l,mid), build(tr[o].son[1],mid+1,r); 35 pushup(o); 36 } 37 inline void pushdown(int o){ 38 if(tr[o].tag<inf){ 39 int lc=tr[o].son[0], rc=tr[o].son[1]; 40 if(!tr[lc].del) tr[lc].dis=min(tr[lc].dis,tr[o].tag), tr[lc].tag=min(tr[lc].tag,tr[o].tag); 41 if(!tr[rc].del) tr[rc].dis=min(tr[rc].dis,tr[o].tag), tr[rc].tag=min(tr[rc].tag,tr[o].tag); 42 tr[o].tag=inf; 43 } 44 } 45 void update(int o,int l,int r){ 46 if(tr[o].del) return; 47 if(L<=l && r<=R){ 48 tr[o].dis=min(tr[o].dis,Dis), tr[o].tag=min(tr[o].tag,Dis); 49 return; 50 } 51 pushdown(o); 52 int mid=(l+r)>>1; 53 if(L<=mid) update(tr[o].son[0],l,mid); 54 if(R>mid) update(tr[o].son[1],mid+1,r); 55 pushup(o); 56 } 57 void Delete(int o,int l,int r){ 58 if(l==r){tr[o].dis=inf; tr[o].del=1; return;} 59 pushdown(o); 60 int mid=(l+r)>>1; 61 if(u<=mid) Delete(tr[o].son[0],l,mid); 62 else Delete(tr[o].son[1],mid+1,r); 63 //printf("Delete:%d %d %lld ",l,r,tr[o].dis); 64 pushup(o); //printf("Delete:%d %d %lld ",l,r,tr[o].dis); 65 pushdel(o); 66 } 67 void query(int o,int l,int r){ //查询最小值的最小下标 68 //printf("query:%d %d %lld ",l,r,tr[o].dis); 69 if(l==r){u=l, Dis=tr[o].dis; return;} 70 pushdown(o); 71 int mid=(l+r)>>1; 72 //printf("query:%d %d %lld %lld %lld ",l,r,tr[o].dis,tr[tr[o].son[0]].dis,tr[tr[o].son[1]].dis); 73 if(tr[o].dis==tr[tr[o].son[0]].dis && !tr[tr[o].son[0]].del) query(tr[o].son[0],l,mid); 74 else if(tr[o].dis==tr[tr[o].son[1]].dis && !tr[tr[o].son[1]].del) query(tr[o].son[1],mid+1,r); 75 } 76 }S; 77 ll ans[N]; 78 void Dij(){ 79 L=R=s, Dis=0; 80 S.cnt=0; 81 S.update(root,1,n); 82 int i; 83 for(int i=1;i<=n;++i){ 84 S.query(root,1,n); 85 ans[u]=Dis; 86 //printf("%d %lld %d %d ",u,ans[u],l[u],r[u]); 87 if(u==t) break; 88 Dis+=z[u]; 89 L=l[u],R=r[u]; 90 S.update(root,1,n); 91 S.Delete(root,1,n); 92 } 93 } 94 int main(){ 95 //freopen("trip9.in","r",stdin); 96 //freopen("trip.out","w",stdout); 97 n=read(),s=read(),t=read(); 98 int i; 99 for(i=1;i<=n;++i) x[i]=read(); 100 for(i=1;i<=n;++i) y[i]=read(); 101 for(i=1;i<=n;++i) z[i]=read(); 102 for(i=1;i<=n;++i){ 103 l[i]=lower_bound(x+1,x+n+1,x[i]-y[i])-x, 104 r[i]=upper_bound(x+1,x+n+1,x[i]+y[i])-x-1; 105 //cout<<i<<' '<<x[i]<<' '<<y[i]<<' '<<l[i]<<' '<<r[i]<<' '; 106 } 107 S.build(root,1,n); 108 Dij(); 109 printf("%lld ",ans[t]); 110 return 0; 111 } 112 /* 113 7 3 7 114 -1 0 1 2 3 5 10 115 11 0 1 1 4 10 2 116 3 1 1 1 2 4 5 117 */
