基本算法思想

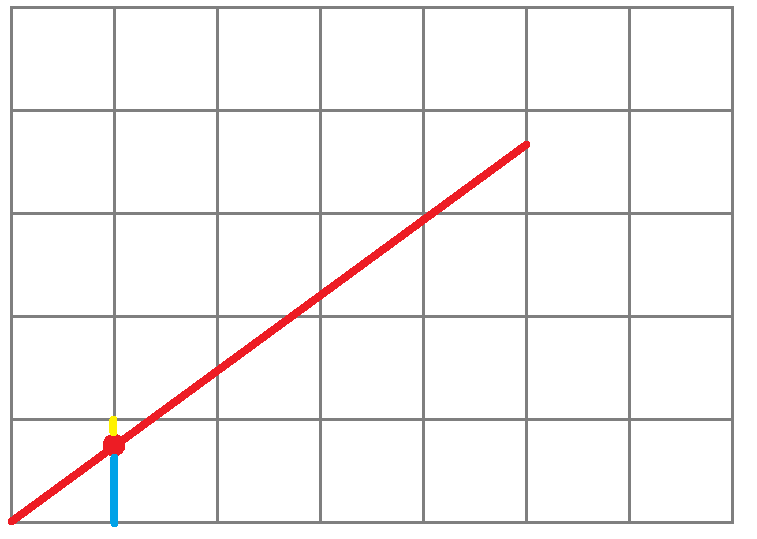
Bresenham直线算法描绘的直线。假设我们需要由 (x1, y1) 这一点,绘画一直线至右上角的另一点(x2, y2),x,y分别代表其水平及垂直坐标。为了一般化,我们假设 x2 - x1 > y2 - y1,那么我们应该如何快速地选择这条线段上最优的网格(绿色),从而绘制出直线呢?
选择原则
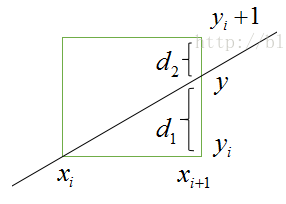
选择的方法就是比较d1,d2的大小
(1)当d1>d2,说明直线上理论点离(xi+1,yi+1)象素较近,下一个象素点应取(xi+1,yi+1)。
(2)当d1<d2,说明直线上理论点离(xi+1,yi)象素较近,则下一个象素点应取(xi+1,yi)。
代码
理解了思想,下面我们直接来看算法代码。http://members.chello.at/easyfilter/bresenham.html
void plotLine(int x0, int y0, int x1, int y1) { int dx = abs(x1-x0), sx = x0<x1 ? 1 : -1; int dy = -abs(y1-y0), sy = y0<y1 ? 1 : -1; int err = dx+dy, e2; /* error value e_xy */ for(;;){ /* loop */ setPixel(x0,y0); if (x0==x1 && y0==y1) break; e2 = 2*err; if (e2 >= dy) { err += dy; x0 += sx; } /* e_xy+e_x > 0 */ if (e2 <= dx) { err += dx; y0 += sy; } /* e_xy+e_y < 0 */ } }
WTF?! 这err是啥意思?怎么跟上面讲的判断原则一点儿也搭不上边啊。。
于是乎本作者查阅了各种微博和技术网页,总算是有所理解。首先上面这个代码非常精简,是可以应对任意象限,任意方向的线段的。同时又加入了优化,基本思想是,将每一个像素点处的小浮点数计算,乘以一个倍数,使得每一步的计算都只有整数计算。
因为各个象限的推导比较繁琐,这里也还是选择第一象限x2 - x1 > y2 - y1,这种一般情况来推导,有兴趣的时候再考虑推导其它的吧。
代码微调
首先我把代码变一下形式,加点儿注释,感觉老外写的不是很合我的胃口。
void plotLine(int x0, int y0, int x1, int y1) { int dx = abs(x1-x0), sx = x0<x1 ? 1 : -1; int dy = abs(y1-y0), sy = y0<y1 ? 1 : -1; int err = dx-dy, e2; for(;;){ setPixel(x0,y0); if (x0==x1 && y0==y1) break; e2 = 2*err; //e2 = 2dx - 2dy if (e2 >= -dy) { err -= dy; x0 += sx; } if (e2 <= dx) { err += dx; y0 += sy; } //首次循环时,e2 <= dx 就是 2dx - 2dy <= dx, 就是dx - dy <= dy } }
算法推导
因为在第一象限,且假设dx > dy(即为上面的 x2 - x1 > y2 - y1), x方向上永远都是会+1,依照选择原则, 我们需要判断的就是y轴方向是否要+1。
那么上面选择原则中描述的d1,d2之间的比较如何对应到代码中的e2 <= dx呢?
看下图
蓝色线段对应d1, 黄色部分对应d2。
传统Bresenham算法,实际上是比较线段与像素分割线交点在一个像素的上半边还是下半边,也就是直接比较图中黄色部分和蓝色部分哪个更长,从而确定下一个像素点的纵坐标是否需要加1。这种长度必定是小于1的,并且是浮点数,不利于计算。
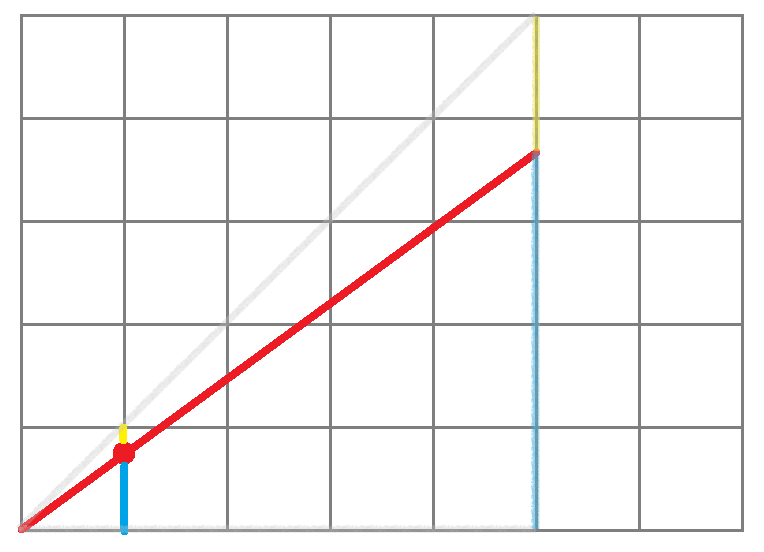
改进后的Bresenham算法,是将原来单个像素内的比较,扩大到整个线段长度上来。如上图中所示,去比较扩大后的黄色部分和蓝色部分哪个更长。如果把线段横坐标变化量记作dx,把纵坐标变化量记作dy的话,根据相似三角形定理,黄色部分的扩大倍数等于蓝色部分的扩大倍数,等于每对三角形的高的扩大倍数,也就是dx倍。这样,我们只需要比较dx-dy与dy的长度,也就是比较dx - dy <= dy,即为源码中的e2 <= dx(详见源码中的注释),也就是上图中的情况,那么就判定下一个像素的纵坐标需要加1。源码中的 y0 += sy 就是做的+1 操作。
那么err是什么呢?
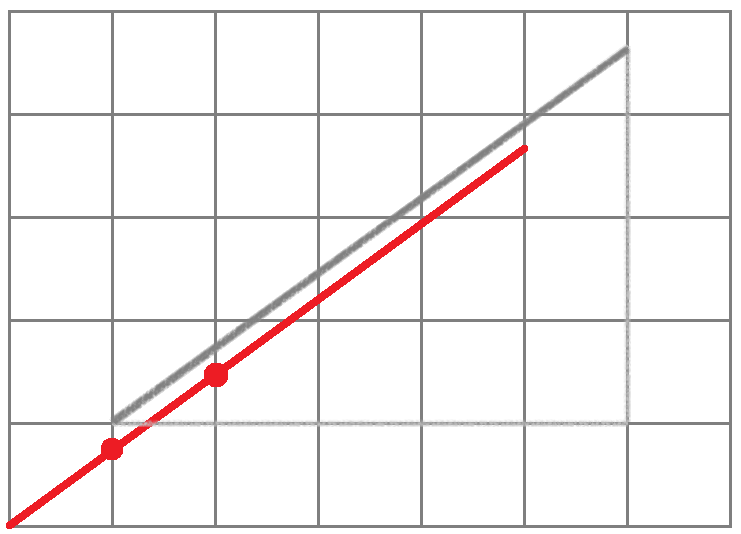
但是,当需要决定下一个像素点的位置时,我们无法再像前一个点那样在对齐像素网格的情况下使用扩大倍数的方法了。因此我们平移该线段,使其经过上一次已确定的像素格点,这样我们就又能利用相似三角形的关系进行扩大再运算了,只是这次的运算稍有不同。
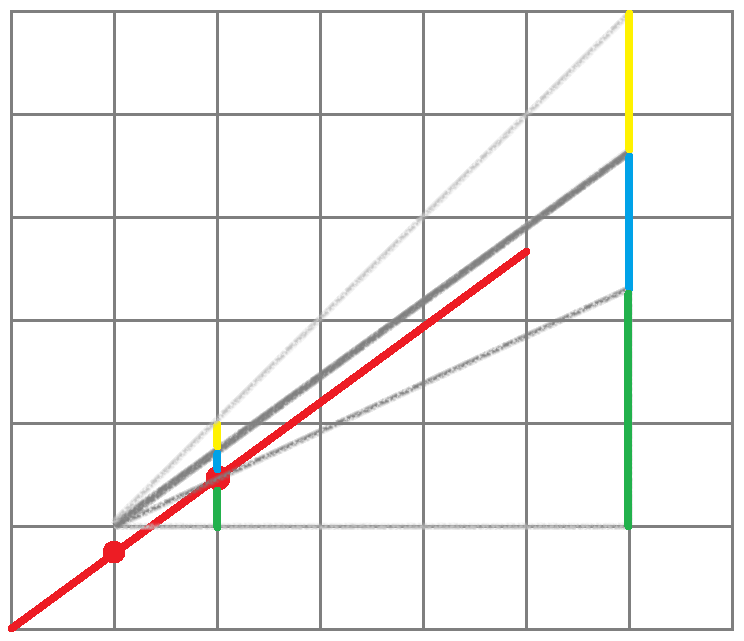
我们可以在上图中发现在一个大的灰色三角形中,有若干相似三角形的存在。其中较深一些的那根线段就是我们为了对齐像素格点而作的辅助线段,它是原线段沿x轴和y轴正方向平移一个单位长度后的线段。平移不改变dx和dy,所以大灰色三角形内相似三角形的扩大倍数依然是dx。现在要想判断下一像素点的位置,只需判断黄色部分加蓝色部分,与绿色部分,哪个大哪个小。实际上就是判断扩大后的黄色部分加蓝色部分,与扩大后的绿色部分,哪个大哪个小。也就是判断如果dx - dy + 扩大后的蓝色部分,比扩大后的绿色部分小的话,下一个像素点的纵坐标就要加1。
这里蓝色部分就是源码中的err。那么之后的像素点纵坐标加1判断就以此类推,流程是:
平移线段到上次确定的像素格点-> 求 dx - dy + err <= dy - err -> 决定下一像素点纵坐标是否加1。
参照源码中
if (e2 >= -dy) { err -= dy; x0 += sx; }
if (e2 <= dx) { err += dx; y0 += sy; }
如果上一次是横坐标加1,纵坐标加1, 就是图片中描述的情景。则原始的err - dy 以后再+dx, 就是dx - dy - dy + dx, 在下一个循环的时候, e2 < = dx, 就变成了 2*(2*dx-2*dy) < = dx, 左右两边变换以后dx - dy + (dx - dy) < = dy - (dx - dy),跟上面的流程中的不等式比较,可见如果横坐标方向加1,纵坐标方向上加1,dx - dy就是err。那么为什么在这种情况下err就是dx - dy呢?
关于err的计算
需要注意的是err这个量的产生原因。我们看到上图中扩大后的蓝色部分err除以扩大倍数dx,就是小的蓝色部分,小蓝色部分的长度就是err/dx。小的蓝色部分恰好是平移后线段与原线段的纵截距差。也就是说,err是由平移线段相对于原线段的纵截距造成的。
实际上我们在每次递推运算的时候,只有第一次平移是基于原线段的,之后并不是从原线段平移出一个线段,而是在上次平移线段的基础上,向下一个确定好的像素点平移。这样,如果要计算当前偏移线段与原线段的纵截距差err/dx,就要先计算本次偏移线段与上次偏移线段的纵截距差,再加上上次偏移线段与原线段的纵截距差,即err/dx要累加起来才是当前偏移线段与原线段的纵截距差,等价于err也要累加。
那么为什么每次原线段都平移到上次确定的像素格点呢?其实平移到其他的格点作辅助线也是可以的,只不过平移到上次确定的格点后,就恰好能通过格点的移动知道本次的偏移量,有利于进行递推运算。
那么每次平移辅助线段之后,造成的这个截距差的变化是多少呢?算出累加后的截距差,也就算出了err,也就可以决定下一像素点纵坐标是否加1了。
考察直线方程:
y = k * x + b, k = dy/dx
变换成一般式,即:
dy * x – dx * y + C = 0, C = dx * b
注意dx,dy皆为常量,是线段横坐标的变化量和纵坐标的变化量,与上文相符。
横纵坐标正向都平移一个单位长度的直线方程:
dy * x – dx * y + C + err = dy * (x - 1) - dx * (y - 1) + C = 0
其中, err = dx - dy,转换为纵截距差的形式:
y = k * x + b + (err/dx) , k = dy/dx
可见线段平移后,截距差恰好是上文中所述的err/dx,而且我们计算出了纵坐标平移一个单位长度后,err = dx,横截距差也就可以计算出来了 err = - dy。正好对应代码中的横坐标变换部分。
if (e2 >= -dy) { err -= dy; x0 += sx; }
到此,在每一步判定流程中未知的err也计算出来了,此时根据上文叙述的相似三角形原理即可通过 dx - dy + err <= dy - err 来判定下一点的纵坐标是否加1。注意,我们现在一直在讨论的是dx>dy的情况,dx<dy的情况类似可证。
参考:
https://blog.csdn.net/u012319493/article/details/53289132
https://www.cs.helsinki.fi/group/goa/mallinnus/lines/bresenh.html