最近做项目遇到曲线拟合的问题,简单做个总结。
1. 曲线拟合
先扔出一点基本概念:
如果已知函数f(x)在若干点xi(i = 1,2,……n)处的值为yi,便可根据插值原理建立插值多项式作为f(x)的近似。但在科学实验和生产实践中,往往会遇到这样一种情况,即节点上的函数值并不是很精确的,这些函数值是由实验或观测得到的数据,不可避免的带有测量误差,如果要求所得的近似函数曲线精确无误的通过所有的点(xi, yi),就会使曲线保留着一切测试误差。所以希望从给定的数据(xi, yi)出发,构造一个近似函数ψ(x),能反映数据的基本趋势即可。
2. 最小二乘法
对于曲线拟合函数ψ(x),不要求其严格的通过所有数据点,也就是说拟合函数ψ(x)在xi处的偏差(亦称残差)不都严格的等于零,即为矛盾方程组:
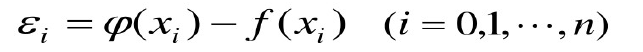
为了是近似曲线能尽量反映所给数据点的变化趋势,要求偏差按照某种度量标准最小。这后面的分析用到了范数的概念,这个不太懂,感兴趣的可以查看《数值分析》相关内容。总之,结论是要求误差的平方和最小,即要求下式具有最小值。

这种方法就叫做曲线拟合的最小二乘法。归根结底是求上式的极小值。
3. 二次函数拟合
假设拟合方程为二次曲线:
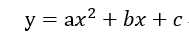
已知数据点(xi, yi),i = 1,2,……n,该近似拟合曲线的均方误差为:
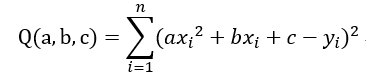
要求上式的极小值,那么归结为多元函数求极值的问题,立刻就会想到求导,则有:
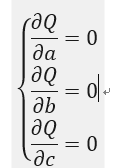
求导过程如下:

可以将上面的结果,将上述线性方程组转换为矩阵方程,即:
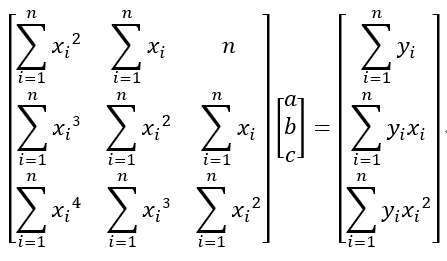
其系数行列式(行列式符号错了,懒得改)为:
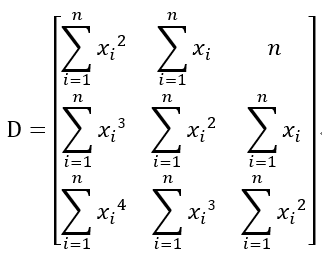
其值若不为0,则方程组有解,另外:
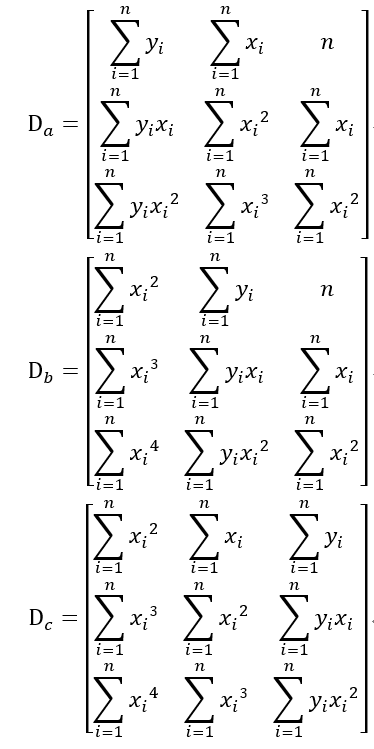
由此可以解得二次曲线的各系数:
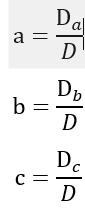
4. 高斯拟合
高斯函数形式如下:

直接采用最小二乘法,其均方误差为:
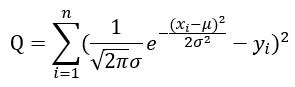
直接这样计算比较复杂,可以先对高斯函数两边求对数,则均方误差可以改写为:
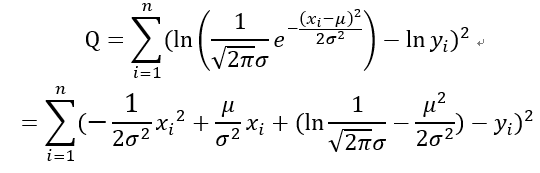
从形式上化为了二次函数,则可用多项式拟合的方法做相应的计算。