转载自quora:
连接:https://www.quora.com/What-is-a-simple-explanation-of-the-Hidden-Markov-Model-algorithm
理解一
通俗的理解就是,每天母亲做的甜点和天气有关。有天气序列,可以观测得到,甜点序列,是我们想知道但是不可以直接知道的(隐层)。
根据以往的数据统计,我们得到一个模型,然后就由三类问题:
1.给定模型(起始状态概率,转移概率, 发射概率),算出某一天吃什么甜点概率最大;(前向后向算法)
2.给定模型和甜点序列,推测什么样的天气序列可能性最大;(维特比算法)
3.给定天气序列,甜点序列,推测什么样的模型,即什么参数能够使得这样天气和甜点对应的概率最大;(EM算法)
Well, to be fair, this really depends on your mom :P Assuming that the heights of mathematical jargon in 'the mom's' dictionary is 'probability', let us try to probabilistically explain what's for dessert based on today's weather. Say the mom can make 3 types of dessert: molten chocolate cake, strawberry shake, and butterscotch icecream. And let us suppose that each day of the week may be classified as either of the following: rainy, dry, or hot. But we have no way of ascertaining what sort of day it is.
We want to develop a model that predicts which dessert the mom is going to prepare on a particular day, if we know the sequence of desserts that she has been making for the past month (say). To make the long story short, the observations (mom's desserts) are dependent on some process which is hidden from our view (the weather).
We assume that each day's weather is dependent on and only on the previous day's weather. This way the sequence of weather description turns out to be a Markov chain. The probability of today weather, given that we know yesterday's weather forms the 'transition probability' of the Markov Chain. For example, if yesterday was rainy, the probabilities of today's weather may be 0.5 for rainy, 0.3 for cold and 0.2 for dry. The matrix formed by taking all such probabilities is called the Transition probability matrix.
Now, we know that mom's dessert depends on each day's weather. Like, if it is rainy, mom is more likely to prepare molten chocolate cake. Hence the probabilities may be 0.7 for molten choc cake, 0.2 for strawberry cake and 0.1 for ice-cream. We construct a matrix containing all such probabilities for all weather conditions. This matrix is called the 'Emission probability matrix'.
There are three questions that may arise out of this scenario and the answers to all three may be arrived at using probability:
1. As I explained earlier, if we know the sequence of observations (desserts) what is the probability that a particular dessert (say ice-cream) may be prepared on a particular day?
2. If we know the sequence of observations (desserts), what is the most likely sequence of weather conditions that would explain the dessert sequence best?
3. If we know the sequence of weather conditions and the sequence of desserts, how can we arrive at the most likely values for the transition probability matrix, the emission probability matrix and the initial matrix*? (*this is simply the probability of the first day in the sequence being rainy/dry/hot.
The first question may be answered using the 'forward-backward algorithm' (in fact, for this question just the forward algorithm is sufficient).The second question may be tackled using the Viterbi algorithm and the third using the Expectation-Maximization algorithm. Does the mom need further explanation?
理解二
参考连接:
chrome-extension://oemmndcbldboiebfnladdacbdfmadadm/https://web.stanford.edu/~jurafsky/slp3/9.pdf
马尔科夫模型从马尔柯夫链讲起。
1.马尔柯夫链:
计算我们观察到的状态序列的概率。但是往往我们感兴趣的状态是不能直接观察到的,就要引入隐马尔科夫模型(HMM)。比如词性标注,我们能看到词语序列,但是我们看不到感兴趣的标注序列。
这是马尔柯夫链的两种表示:
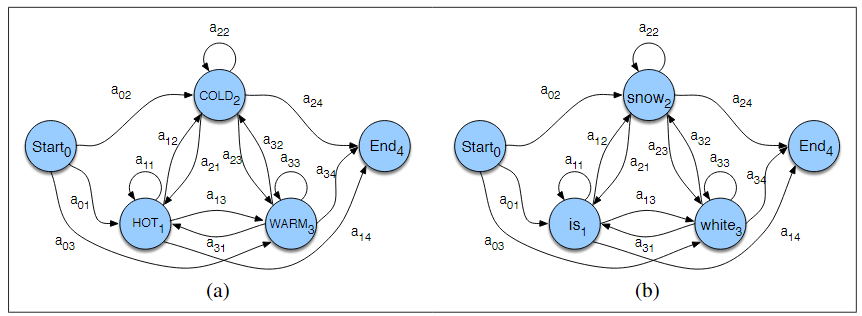

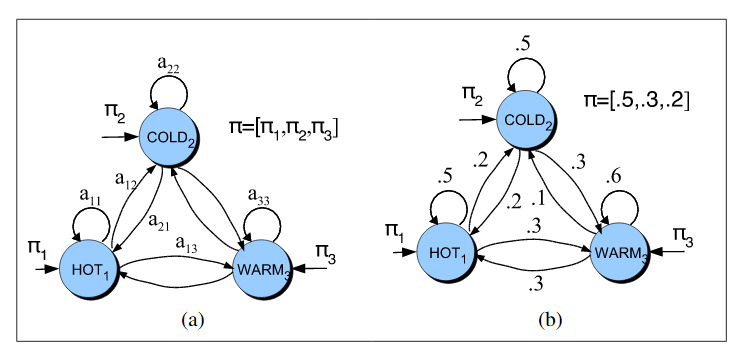

两种方式的区别就是,第一种给定马尔柯夫链的起始和结束状态,第二种不给,但是给出在各个状态起始的概率π(应该也是给出了转移概率的,图中可以看到)。
2.HMM
让我们能够计算可以看见的状态,事件,也可以和计算隐藏的状态和事件;
马尔科夫的一个规范化定义:

和马尔柯夫链一样,HMM也有一个替代的表示方法,来表示那血不受起始状态约束的HMM:

隐含马尔科夫模型HMM有两个假设:
1)每个状态只和他的前一个状态有关
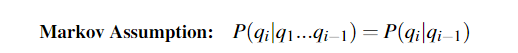
2)每个观测输出只依赖于产生这个输出的状态:

例子:
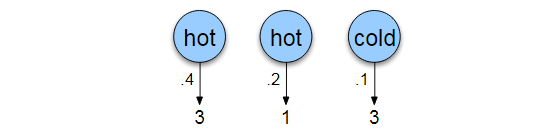
我们想知道北京2017年7月的气温情况,但是没有记录,只有记录小明同学这个夏天吃冰淇淋的情况。根据他以前吃冰淇淋和天气的历史纪录,可以建立一个模型,利用小明每天吃冰淇淋的数目(观测状态),来推测每天的天气(隐含状态)。为了简单,天气只有hot,cold,每天吃冰淇淋是整数。
建立如下HMM模型:
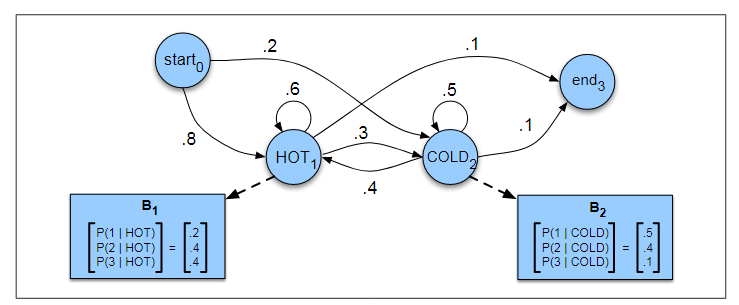
图中的表格,概率表示的是发射概率,就是给定状态下产生特定观察状态的概率;
有了HMM的结构之后,就可以讨论能够对这个结构做哪些计算了:
一般分为三种计算,计算观测状态的概率,计算隐含状态的概率(推测),计算最佳模型。就是前面第一个理解讲的三个问题;

3.HMM第一个问题-计算观察状态概率

方法一:
直接计算概率乘机,复杂度高,指数级:
马尔柯夫链和隐含马尔克付模型的区别:
我们对表层状态的观察就是隐含的状态序列,直接根据起始状态和转移概率乘机就可以得到我们的答案;
对于HMM就不是这么简单,因为有很多种可能的隐含状态序列可以产生我们需要的状态序列输出;

计算推到过程:
根据我们前面的两个假设之一,输出只和产生输出的隐含状态有关,所以给定状态观测序列和状态序列就能计算条件概率:
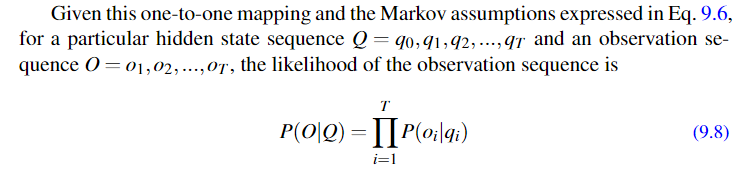
比如:

当然,上面的是理想情况,给出了与隐含的状态序列,但是事实上我们不知道这些序列,所以需要计算所有的可能。并且给每种可能乘以这种可能性出现的概率,即P(Q),所以引入了联合概率分布;
根据这里采用计算算法的策略不同,就产生了后面的前向算法。
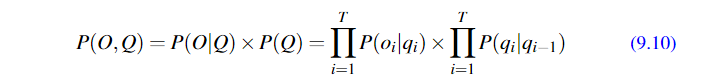
比如:

根据全概率公式:
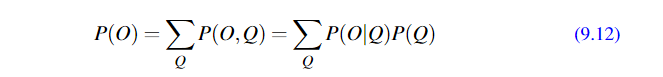
比如:
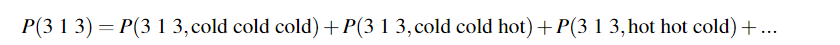
这里状态数N = 2,观测序列长度T = 3, 所以需要计算 2^3 = 8个概率;
这里的复杂度很大:
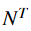
所以这里如果优化一下,就有了下面的前向算法,复杂度:
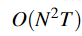
方法二:
使用前向-后向算法,复杂度低:多项式级别:
主要利用的动态规划的理论,把前面计算过的概率存储,后面不需要重复计算:
两种图形表示方法:
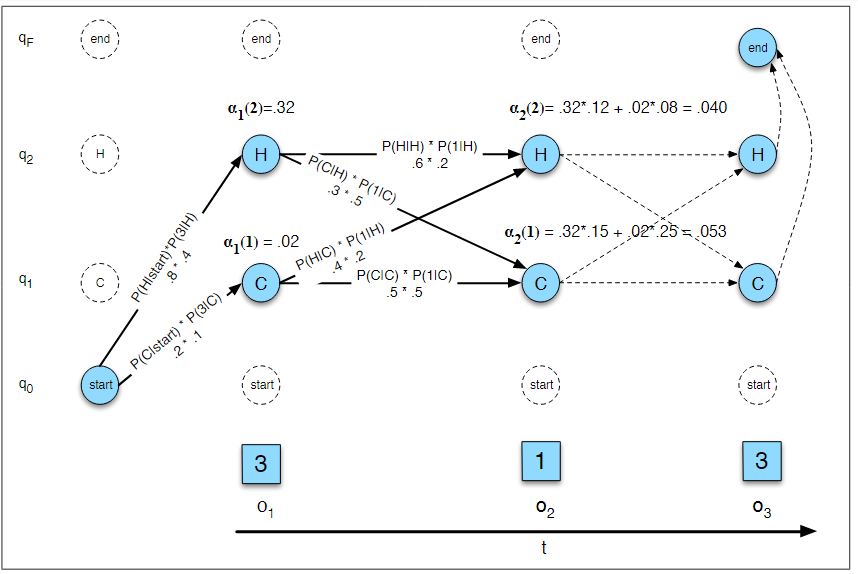
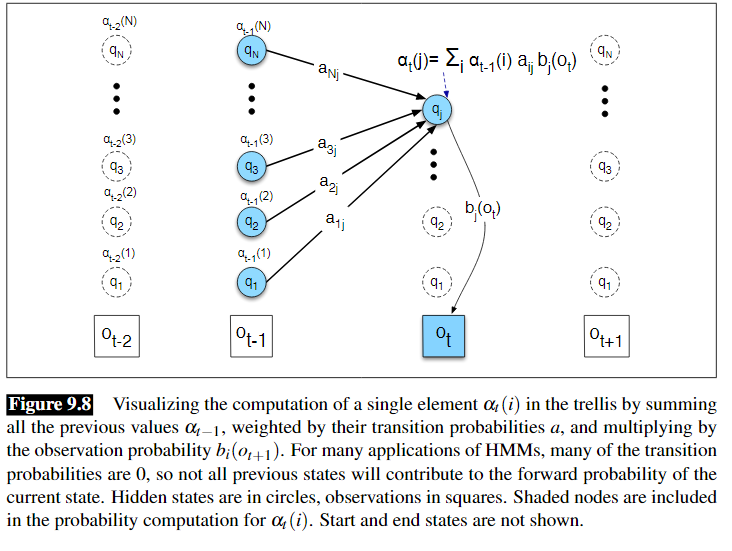
接下来给出定义和推到:
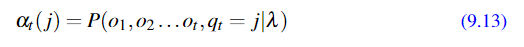
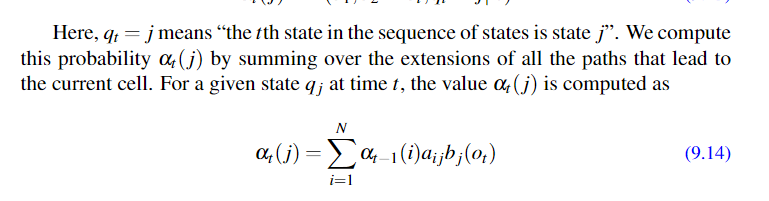

定义:

算法伪代码:

4.HMM第二个问题-计算隐含状态概率(预测问题)
这部分考虑的是如何给定模型和观察序列O,推测最有可能的隐含状态。比如给定小明吃的冰淇淋数量序列,推测这段时间的最有可能的天气状态序列。
简单的考虑,可以列举出所有的可能状态序列,比如序列长度是10,每天有两种可能,hot,cold,所以有2^10-1024种可能,利用前向算法计算出这么多状态产生我们观测序列的概率,选取最大的一个状态序列就可以。但是不可行,因为这是指数级别的算法,效率太低。
所以引入以动态规划为基本思想的维特比算法。

算法的具体定义伪代码:

维特比算法和前向算法之间的区别:
1)维特比算法求每个时间点的概率的时候是在以前路径概率上求最大值,max(),但是前向算法是求和sum();
2)维特比算法有一个backpointer【t,i】代表当前时间点 t 前一个时间点 t-1 的状态 i,因为维特比的任务是要输出最有可能的路径,但那时前向算法只需要计算概率大小;
5.HMM第三个问题-计算模型的参数