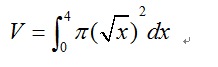定积分一个广泛的应用就是在求解一些“看似不规则”的几何体的体积,之所以说看似不规则,是因为不规则之下还是有一定的“规则性”可言的,我们就是需要抓住这些线索进行积分运算得到体积。
方法1:切片法。

这里由于处理的方法思想和典型的离散的黎曼和到连续的积分的过程类似,因此这里不再重复推导,直接给出如何应用以及实例。
基于这条定理,我们能够直接介绍一下卡瓦列里原理。卡瓦列里原理表明,高度相同并且在每个高度上的横截面积相同的几何体的体积相同,直观的理解,就像下面这两堆“叠硬币”图。

下面我们看一些实例。
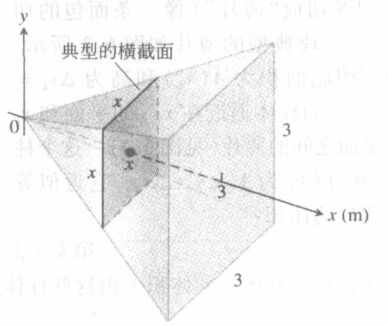
利用这种方法的计算体积具有较为严苛的限制,其中最重要的一点是,这个不规则几何体的横截面A(x)是典型的几何图形,利用这种方法计算体积能够归纳成如下的算法流程:
- 画出立体和典型的横截面草图
- 求典型横截面面积A(x)
- 求积分限
- 利用微积分基本定理求A(x)的积分
那么对于这个例子,基于草图的基础上,能够列出如下的定积分式:
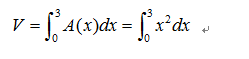
再来看一个稍微有挑战性的图。

选择横截面是有技巧的,一个关键原则是选择的这个横截面沿积分变量所在的坐标轴移动的时候,横截面需要一直保持是典型平面图形的形式。依旧将x作为积分变量,则横截面A(x)是矩形,于是我们能够列出如下的式子:
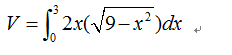
方法2:
处理旋转体的圆盘方法。
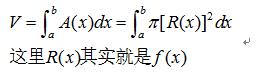
其实这种方法本质上讲是一种处理旋转体的切片法。在介绍这种方法之前,有必要先介绍一下什么是旋转体:将某平面图形绕坐标轴旋转一周形成的空间几何体我们称之为旋转体。
旋转体非常的有规律可循,假设我们旋转是曲线f(x)和x轴围成的曲边梯形,我们能够发现,将x视为积分变量,横截面处处是典型的图形——圆,而半径恰好可以通过曲线f(x)给出。
让我们看几个实例。
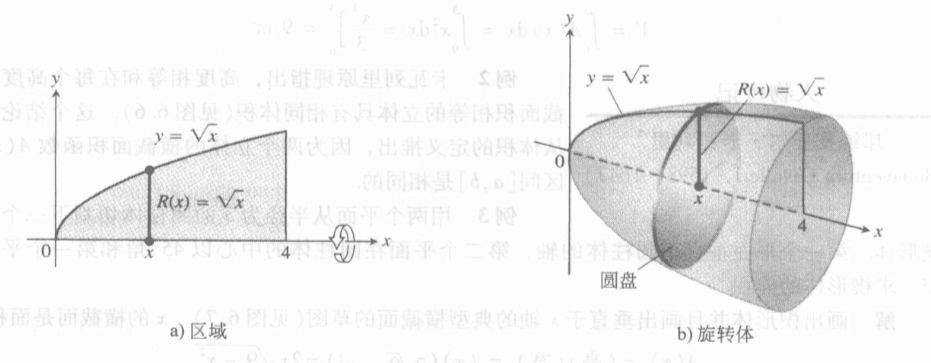
容易列出如下的定积分式。