在连续随机变量这部分,有一种特殊的随机变量X,对于X所有可能取值,P(X)都相等,我们称其为均匀随机变量。
基于均匀随机变量的定义,我们容易看到,其密度函数f(x)必然是一条平行于x轴的直线,因为这样才能够保证如下等式成立。
对于X∈[a,b]的随机变量,我们能够直接得到其密度函数是f(x)=1/(b-a),x∈[a,b].
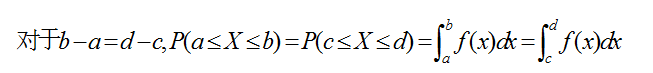
下面我们来看一个均匀随机变量的例子。
Q:向一个圆当中随机取一条弦,这条弦比该圆内接正三角形的边长要长的概率是多少?
分析:这其实是1889年法国数学家贝特朗提出的贝特朗悖论。
按照一般解决概率问题的策略,我们首相应该给出样本空间。
法一:样本空间Ω1={x|x为弦到圆心的距离}
法二:样本空间Ω2={x|x过弦端点的切线和弦围成的角度}
容易看到,对于不同的样本空间的定义方法,最终得到的结果是不同的。对于法一是1/2,对于法二的概率是1/3。
Q2(uva 12230):
给出A、B两点之间的距离,以及两点之间n条河的坐标、宽度以及该河上自动船的速度(河均与A、B两点连线垂直),人在平地行进的速度是1,人从A到B所需的时间的期望(船的停泊完全随机)。
分析:这道问题基于期望的数学概念,突破口就是找到均匀分布这个分布模型。我们先从任意一条河分析起,过该条河的最短时间是L/v,也就是说已到达这条河的岸边,船也刚好到岸,而过该条河最长时间是3L/v,也就是说刚到达这条河的岸边,船刚好开走,也就是说设随机变量X表示过该条河的时间,那么X∈[L/v , 3L/v],题目中又说船的停泊完全随机,因此X符合[L/v,3L/v]的均匀分布,那么易得,过该河的时间期望E[X]=2L/v.
对于剩余n-1条河的时间期望,采取相同的策略。再加上陆地上行走的时间D-sum(L)即可。