在之前初步介绍图的文章中,我们得知,图(graph)是表征事物之间关系的一种抽象化表示方法,而基于图的概念,我们将所有的无回路无向图拿出来,给它们一个新的名字——树。
关于树的概念性术语很多,这里我们先就简单的二叉树(一个根至多有两个子树)来进行分析。
这就是一些简单的二叉树,这里A、B、C等我们成为节点。A叫做根节点,它的两个分支是B和C,并且我们称B是一个左子树,C是一个右子树,知道了这些简单的概念,我们就可以初步的探讨一些问题了。
二叉树树作为一种特殊的图,我们也要研究其遍历的方式,正如我们研究一般的图的遍历方式。由于其基本结构包括根、左子树、右子树,所以我们遍历的时候可以改变这三个元素的输出方式来得到不同的遍历顺序。
前序遍历的递归定义:对于一个节点,访问并输出根的信息;按照前序遍历左子树;按照前序遍历右子树。
中序遍历的递归定义:对于一个节点,按照中序遍历左子树;访问输出根的信息;按照中序遍历右子树。
后序遍历的递归定义:对于一个节点,按照后序遍历左子树;按照后序遍历右子树;访问并输出根的信息。
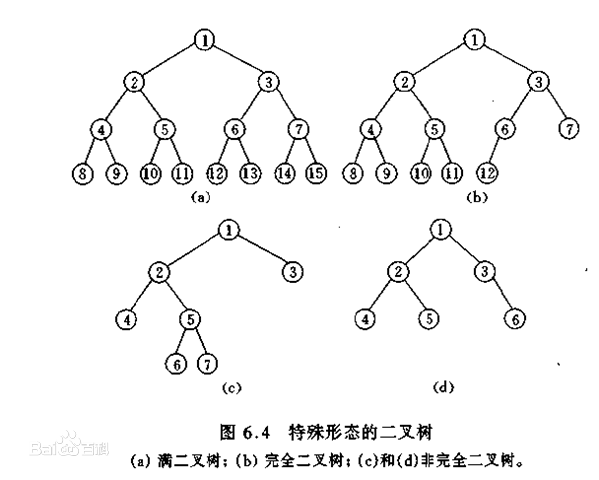
拿上图d举个例子,前序遍历:124536,;中序遍历:425361;后序遍历:452631。
值得注意的是,除了中序遍历,其余两种遍历方式可以推广到k叉树,因为对于中序遍历,每当遍历完左子树,都会访问一次根节点,这样会造成多次重复访问根节点,就谈不上“遍历”这二字了。
而且对于一个给定前(后)序遍历和中序遍历的二叉树,是可以唯一确定的。
那么我们来看一道关于二叉树这三种遍历的题目(Problem source :pku2255)
Description
D
/
/
B E
/
/
A C G
/
/
F
To record her trees for future generations, she wrote down two strings for each tree: a preorder traversal (root, left subtree, right subtree) and an inorder traversal (left subtree, root, right subtree). For the tree drawn above the preorder traversal is DBACEGF and the inorder traversal is ABCDEFG. She thought that such a pair of strings would give enough information to reconstruct the tree later (but she never tried it). Now, years later, looking again at the strings, she realized that reconstructing the trees was indeed possible, but only because she never had used the same letter twice in the same tree. However, doing the reconstruction by hand, soon turned out to be tedious. So now she asks you to write a program that does the job for her!
Input
Output
题目大意:给出一个二叉树的前序遍历、中序遍历,让你输出其后序遍历。
数理分析:根据其定义,三种遍历方式是通过递归生成的,那么现在知道了两种遍历方式,也是可以还原出原来的二叉树的。
举个例子,拿第一组数据来说,前序遍历为DBACEGF,中序遍历为ABCDEFG,那么我们通过前序遍历的定义,可知D是最大的那棵树的根,此时我们再通过中序遍历,ABC在D的左端,是左子树,而EFG在D的右端,为右子树,这样可以初步画一个树。然后我们在找前序遍历的第二个点……最终一定会还原出原来的二叉树。
这里题目要求直接输出后序遍历,那么我们在还原二叉树的同时也能构造出后序遍历。在起始情况中,前序遍历的第一个点作为整棵树的根,是要作为后序遍历的最后一个点的,这是我们再通过中序遍历和前序遍历找到此根下的右子树,我们把右子树看成一个整体,通过前序遍历又能找到一个根,再通过此根和中序遍历,分出左子树和右子树……直到这个根没有子树。
随后构造左子树。
这里之所先找根再找右子树在找左子树,是和后序遍历的递归概念呼应的。
编程实现:通过以上的描述,构造过程本质上是一种递归,也可以说是遍历图我们所熟悉的深搜。
参考代码如下。
#include<iostream> #include<string.h> using namespace std; char preorder[30]; char midorder[30]; char postorder[30]; int len; void travel(int preStar,int preEnd ,int midStar , int midEnd) { if(preStar > preEnd) return; postorder[--len] = preorder[preStar]; //记录根 if(preStar == preEnd) return; int i; for(i = 0;i <= midEnd;i++) if(midorder[i] == preorder[preStar]) break; travel(preStar + i - midStar + 1,preEnd, i + 1, midEnd); //左子树 travel(preStar + 1 , preStar + i - midStar , midStar , i - 1);//右子树 } int main() { while(cin>>preorder>>midorder) { len = strlen(preorder); postorder[len] = '�'; travel(0,len-1,0,len-1); cout << postorder<<endl; } }
我们这里下面将介绍一些树形结构在储存信息方面的一些其他应用。
首先我们介绍线段树。
线段树,顾名思义,一定是和线段有关的,我们通过一条线段[1,n]上的整数点储存信息,然后通过二分的方法形成完全二叉树来储存这些信息,并且还可以进行访问查找、更新数据等一系列操作,在后面具体问题的分析中我们都将讨论到。
线段树能够解决很多的问题,这里我们从一个简单的问题来入门线段树的学习——求指定区间的最大值问题。(Problem source : hdu1754)
不管你喜不喜欢,现在需要你做的是,就是按照老师的要求,写一个程序,模拟老师的询问。当然,老师有时候需要更新某位同学的成绩。
题目大意很明了,数理分析也没有难度,那么这里我们重点分析它的编程实现。
我们先将整个问题进行功能划分,然后再考虑函数模块化的实现。在上述问题中,我们要完成数据的存储、访问数据得到最大值、更新数据。
这里也许人们会考虑直接用数组进行记录然后遍历求最大值,但是这种方法,第一,暴力穷举时间复杂度太高;第二,这种方法是很难完成对数据的更新。所以这里我们考虑构造线段树。
数据的存储:也就是我们说的建立一棵树。这里我们将用二分加深搜(dfs)进行构造,并在每个非叶节点记录其左子树和右子树的最大值,这里是通过深搜后再回溯来实现的。此时,我们若将n个人的分数看做线段[1,n]上整数的“携带”的信息,那么整棵树构造完成后,每个非叶节点都记录着某个区间段上的最大值。
访问数据得到最大值:这里我们依然需要采用二分的查找思想,然后将所求区间与我们构造出的线段树记录的信息进行匹配,得到答案。
更新数据:这里依然基于二分查找(因为构造线段树的时候就是用的二分法,这与我们所构造的线段是本质上是完全二叉树是呼应的),一旦找到所在的叶节点,便进行数据的更新,然后进行和建树时一样的回溯操作把整个书的节点都要更新一遍。
有了以上对编程过程的分析,再理解代码就不困难了。
参考代码如下。(代码中又>>和<<操作,无非是/2或*2,这里是为了得到线段树在对应的数组里的下标,读者稍微模拟一下就可以知道代码中为什么要这么写)。
#include<cstdio> #include<cmath> using namespace std; int Max[4000001]; int max(int a , int b) { return a>b?a:b; } void Pushup(int index) //回溯构造线段树 { Max[index] = max(Max[index<<1],Max[(index<<1)+1]); } void build(int l,int r,int index) //建立线段树 { if(l == r) { scanf("%d",&Max[index]); return; } int m = (l + r)>>1; build(l,m,index<<1); build(m+1,r,(index<<1)+1); Pushup(index); } void update(int p,int q,int l,int r,int index)//更新数据 { if(l == r) { Max[index] = q; return; } int m = (r+l)>>1; if(p <= m ) update(p,q,l,m,index<<1); else update(p,q,m+1,r,(index<<1)+1); Pushup(index); } int getMax(int L,int R,int l,int r,int index)//访问给定区间的数据 { if(L<=l && R >= r) return Max[index]; int m = (r+l)>>1; int ret = 0; if(L <= m) ret = max(ret,getMax(L,R,l,m,index<<1)); if(R > m) ret = max(ret,getMax(L,R,m+1,r,(index<<1)+1)); return ret; } int main() { int n , m , a , b , i; char c; while(scanf("%d%d",&n,&m) != EOF) { build(1,n,1); for(i = 0;i < m;i++) { scanf("%*c%c%d %d",&c,&a,&b); if(c == 'Q') printf("%d ",getMax(a,b,1,n,1)); else update(a,b,1,n,1); } } }
下面我们介绍有关生成树的概念与算法。
对于给定的图G<V,E>,有树形图T<V',E'>是G的子图,并且有V' = V,那么我们就成T是G的生成树,而在G的众多生成树中,总存在一个生成树T',是的边集E'的权值之和最小值,那么则称这个T'是G的最小生成树。
最小生成树在实际的生产生活中有着很重要的应用,举个很简单的例子——交通系统(其实发现图论的很多东西都可以用在交通系统方面)。它的一个最简单的模型,对于含有n个城市的交通网络,如何给出一种方案使得道路的造价最小而且可以使这n个城市依然保持连通,其实本质上就是求解最小生成树的问题。
在这里介绍Prime算法来求解一个图的最小生成树并计算其权值之和。
其实Prime算法很类似在求解一个图的单源最短路径的Dijkstra算法,是基于一种贪心的思想或者动态维护最优情况的思想。
基于我们对Dijkstra算法的学习,我们知道,需求的最短路径的边数的最大值是确定的,那么我们便一次为基准进行遍历。同样,在这里我们容易看到,对于最小生成树T,其边的数量固定的,我们同样可以以此为基准,进行n-1次构造来完成对最小生成树的寻找。
对于G图的点集V,开始我们任取一点v1,作为构造最小生成树的起点,我们构造lowcost[i]数组,用以记录v1到vi的边的权值(这里的边是直接连着v1和vi),我们找到min(lowcost[2],lowcost[3],……,lowcost[n]),假设找到vj到v1的权值最小,那么vj和边v1vj添加到最小生成树当中完成一次构造,再以vj为初始点,重复上述步骤。
再进行n-2次构造,便可完成最小生成树的构造。
其实这个过程就是模拟一个贪心策略,访问点集V,遍历n-1次来构造最小生成树中n-1条边,当然每次只需找到权值最小的边即可。
我们通过一个题目来具体实现一下用于求解最小生成树的Prime算法。(Problem source : hdu 1102)
基于上文对该算法的论述,简单的模拟不难实现,需要一提的是,这里标记边长我们利用一个很大的书INF作为一个标准,当然也可以设置一个数组visit来进行表及操作。 参考代码如下。
#include<iostream>
#include<cstdio>
#include<string.h>
using namespace std;
const int MAX = 105;
const int INF = 9999999;
int Map[MAX][MAX];
int N , lowcost[MAX],road;
void prime()
{
for(int i = 2;i <= N;i++)
lowcost[i] = Map[1][i];
for(int i = 2;i <= N;i++)
{
int temp = lowcost[i] , k = i;
for(int j = 2;j <= N;j++)
if(temp > lowcost[j])
{
temp = lowcost[j];
k = j;
}
road += temp;
lowcost[k] = INF;
for(int j = 2;j <= N ;j++)
if(Map[k][j] < lowcost[j] && lowcost[j]<INF)
lowcost[j] = Map[k][j];
}
}
void makeSet(int n)
{
for(int i = 1;i <= n;i++)
for(int j = 1;j <= n;j++)
cin>>Map[i][j];
}
int main()
{
int Q , m , n ;
while(cin >> N)
{
road = 0;
makeSet(N);
cin>>Q;
while(Q--)
{
cin >> m>>n;
Map[m][n] = Map[n][m] = 0;
}
prime();
cout << road <<endl;
}
}
下面一份利用visit[]数组进行标记操作的Prime算法。(不是此题的AC代码,需要稍加修饰)
#include<iostream> #include<cstdio> #include<cstring> #include<string> #include<algorithm> using namespace std; #define INF 0x3f3f3f3f #define MAXN 110 int map[MAXN][MAXN], lowcost[MAXN]; bool visit[MAXN]; int nodenum, sum; void prim() { int temp, k; sum = 0; memset(visit, false, sizeof(visit)); //初始化visit visit[1] = true; for(int i = 1; i <= nodenum; ++i) //初始化lowcost[i] lowcost[i] = map[1][i]; for(int i = 1; i <= nodenum; ++i)//找生成树集合点集相连最小权值的边 { temp = INF; for(int j = 1; j <= nodenum; ++j) if(!visit[j] && temp > lowcost[j]) temp = lowcost[k = j]; if(temp == INF) break; visit[k] = true; //加入最小生成树集合 sum += temp;//记录权值之和 for(int j = 1; j <= nodenum; ++j) //更新lowcost数组 if(!visit[j] && lowcost[j] > map[k][j]) lowcost[j] = map[k][j]; } } int main() { int a, b, cost, edgenum; while(scanf("%d", &nodenum) && nodenum) { memset(map, INF, sizeof(map)); edgenum = nodenum * (nodenum - 1) / 2; for(int i = 1; i <= edgenum; ++i) //输入边的信息 { scanf("%d%d%d", &a, &b, &cost); if(cost < map[a][b]) map[a][b] = map[b][a] = cost; } prim(); printf("%d ", sum); //最小生成树权值之和 } return 0;
上文中我们讨论了求解最小生成树的prime算法,这里再给出基于并查集的kruskal算法。
如果概述一下kruskal算法的过程,非常简单。给出一个n阶图G,我们按照从小到大的顺序给边的权值排序,去掉G中所有的边,按照排序后的边依次往图中添加边,如果当前添加的边使得G中出现了回路,则不添加这条边,构造结束之后,如果新图G’满足边数m = n - 1,则G'即为G的最小生成树。
其实kruskal算法也是基于贪心算法,显然对于G的生成树,我们需要构造n - 1条边,如果这条边使得生成树产生了回路,说明这条边是不需要的,而对于不会产生回路的边,我们只需要从权值最小的边开始选择即可。
在编程实现上,我们是需要基于并查集访问根节点的算法的。在上述对算法过程的描述中,如何判断添加了当前没有被选择的边集中权值最小的边时,是否让生成树产生了图呢?就在这里用到了并查集。对于该过程中我们选择的权值最小边,我们访问这条边连接的两个节点u、v,如果这两个节点的根节点相同,那么表明这两个点已经出现在生成树的一条通路上了,由于不可能访问该边两次,所以此时连接这两个点u、v,则一定会形成回路。
基于上文的分析,我们通过一个具体而简单的题目来对kruskal算法进行编程实现。(Problem source : hdu 1863)
容易看到,这是很典型的求解一个G图的最小生成树并访问权值的问题。值得注意的是,题目给出的G图不一定存在最小生成树,即该图不一定是连通的,因此在构造最小生成树的时候只需设置一个参量ant用来记录当前构造图的边数,如果最终满足ant != n - 1(n为G的阶数),则表明不存在最小生成树。
参考代码如下。
#include<stdio.h> #include<stdlib.h> #include<algorithm> using namespace std; #define N 105 int n , m , ans , ant , v[N],u[N],w[N],f[N],r[N]; int cmp(int i , int j) { return w[i] < w[j]; } int Find(int x) //并查集:访问某个节点的根节点 { return f[x] == x ? x :f[x] = Find(f[x]); } int kruskal() { int fx , fy , ans = 0 , ant = 0; for(int i = 0;i <= n;i++) f[i] = i; //初始化各个节点的根节点 for(int i = 1;i <= n;i++) r[i] = i; //该数组用于记录边的序号 sort(r , r + n , cmp);//排序,此时r[]记录的边的序号,按照权值由小到大的顺序 for(int i = 1;i <= n;i++) { int t = r[i]; fx = Find(u[t]);//访问当前构造过程权值最小的边的两个节点的根节点 fy = Find(v[t]); if(fx!=fy) //判断是否形成了回路 { ans += w[t]; f[fx] = fy; ant++; //记录当前图中的边数 } } if(ant < m - 1) //判断是否连通 ans = 0; return ans; } int main() { int sum; while(scanf("%d%d",&n,&m)!= EOF && n) { for(int i = 1;i <= n ;i++) scanf("%d%d%d",&u[i],&v[i],&w[i]); sum = kruskal(); if(sum) printf("%d ",sum); else printf("? "); } }
了解了求解最小生成树的两个算法,我们会想,G图的所有生成树,除去了最小生成树,权值最小的生成树的权值之和是多少呢?或者对于一个图G,它的最小生成树是否唯一呢?这里就要一个新的概念——次小生成树。
次小生成树的概念顾名思义,就是G图所有的生成树中权值第二小的生成树。那么我们如何来得到这个次小生成树呢?
我们现在容易得到图G的最小生成树,而次小生成树的权值又是与最小生成树最相近的,那么我们就可以基于最小生成树来构建次小生成树。首先我们明确,次小生成树只需要在最小生成树的基础上,用一个不在最小生成树T中的边<u,v>替换一个T中的边<u',v'>,使得两边的权值之差最小,并没有影响生成树的连通性,那么替换后的T'便是G的次小生成树。
显然,由于我们是基于最小生成树T进行构造,所以无论如何操作,新图T'的权值都是要增加的,而我们用如果用矩阵将点u、v路径之间权值最大的边记录下来,那么我们在从那些不属于T但是属于G的边来构造次小生成树的时候。显然是要与矩阵记录的u、v之间权值最大的边进行交换,这显然是选择<u,v>(∈G,∉T)与最小生成树中对应的<u,v>'所有方案中最优的方案,这是一步枚举的优化。
那么我们只需要再枚举任意边<u,v>(∉T,∈G),并维持一个T'权值的最小值,我们即可以得到图G的次小生成树T'。
因此我们不难概括出次小生成树的算法步骤:
1)先用prim求出最小生成树T,在prim的同时,用一个矩阵max[u][v]记录在树中连接u-v的路径中权值最大的边.
2)枚举所有不在T中的边u-v,加入边u-v,删除权值为max[u][v]的边,不断枚举找到次小生成树。
不难看出,次小生成树其实就是一个基于最小生成树然后枚举边维持权值最小的一个算法。那么了解了如何求解次小生成树,我们不妨通过一个问题来看看它又怎样的应用。(Problem source : 1679)
Description
Definition 1 (Spanning Tree): Consider a connected, undirected graph G = (V, E). A spanning tree of G is a subgraph of G, say T = (V', E'), with the following properties: 1. V' = V. 2. T is connected and acyclic.
Definition 2 (Minimum Spanning Tree): Consider an edge-weighted, connected, undirected graph G = (V, E). The minimum spanning tree T = (V, E') of G is the spanning tree that has the smallest total cost. The total cost of T means the sum of the weights on all the edges in E'.
Input
Output
题目大意:给定一个图G,让你判断该图的最小生成树是否唯一,如果唯一则输出其权值。
数理分析:其实关于判断一个图是否有唯一的最小生成树,在上文引入次小生成树的概念中已经买下了伏笔,我们如果求解次小生成树,发现权值之和与次小生成树相等,那么显然该图次小生成树是不唯一的。因为我们基于以上的算法,构造的T'与T一定是非同构的,而T如果与T'的权值又相同,那么说明图G的最小生成树是不唯一的。
有了以上的算法分析,结合一定的编程技巧,不难将其实现。
参考代码如下。
#include<iostream> #include<cstring> #include<cstdio> using namespace std; const int INF=0x3f3f3f3f; int g[110][110],dist[110],mmax[110][110]; int pre[110]; bool mark[110]; bool connect[110][110]; int mst,mint; int n,m; int prim() { int res=0,fa,p,min,i,j; memset(mmax,0,sizeof(mmax)); for(i=1;i<=n;i++) { dist[i]=g[1][i]; pre[i]=1; mark[i]=false; } dist[1]=0; mark[1]=true; for(i=1;i<n;i++) { p=-1;min=INF; for(j=1;j<=n;j++) { if(!mark[j]&&dist[j]<min) { p=j; min=dist[j]; } } if(p==-1) return res; mark[p]=true; res+=dist[p]; fa=pre[p]; connect[fa][p]=false; connect[p][fa]=false; mmax[fa][p]=min; for(j=1;j<=n;j++) mmax[j][p]=(mmax[fa][p]>mmax[j][fa])?mmax[fa][p]:mmax[j][fa]; for(j=1;j<=n;j++) { if(!mark[j]&&dist[j]>g[p][j]) { dist[j]=g[p][j]; pre[j]=p; } } } return res; } int main() { int tc; //freopen("1.txt","r",stdin); scanf("%d",&tc); while(tc--) { scanf("%d %d",&n,&m); memset(g,INF,sizeof(g)); memset(connect,false,sizeof(connect)); while(m--) { int u,v,c; scanf("%d %d %d",&u,&v,&c); g[u][v]=c; g[v][u]=c; connect[u][v]=true; connect[v][u]=true; } mst=prim(); int i,j; bool flag=false; for(i=1;i<=n;i++) for(j=1;j<=n;j++) { if(connect[i][j]==false||g[i][j]==INF) continue; if(g[i][j]==mmax[i][j]) { flag=true; break; } } if(flag) printf("Not Unique! "); else printf("%d ",mst); } return 0; }