写在前面:当时开计算几何这个专题神奇的从解析几何开始了,然后最近发现《计算几何及应用(金博)》这本书前面那章忽略掉了一些重要的东西比如说点定位、半平面相交之类的东西,恰好还有一些和计算几何扯上边但是不需要算法的简单题目没有整理,故在此开辟一块小空间。
我们再来看一道有关几何的问题。(Problem source:hdu2073)
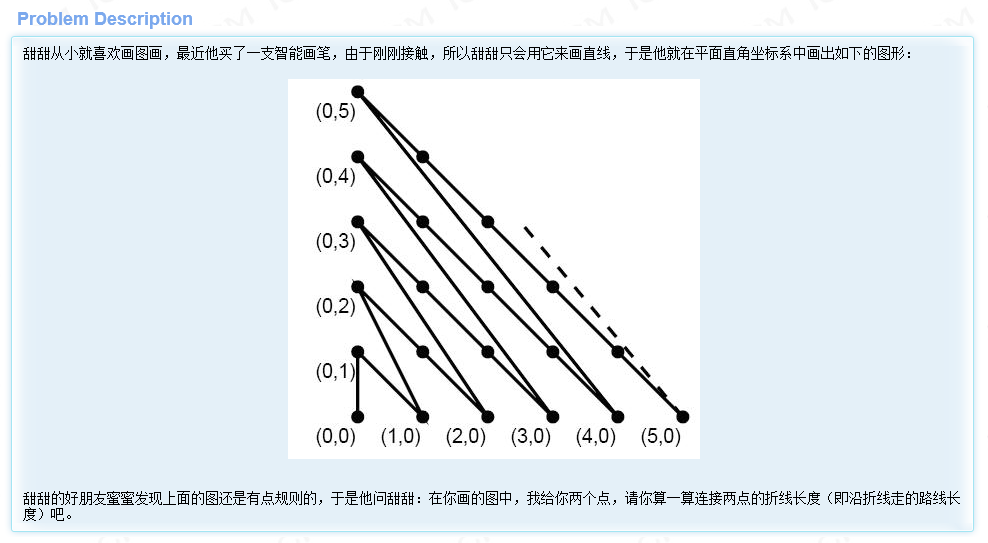
数理分析:虽然这道题异常的简单,基本算不上计算几何这个专题当中的题目,但是把它拿到这里来,是源于这道简单几何题的思路其实体现了计算几何整个体系中比较重要的思维。
这里给出两个点的坐标,我们其实只需找到这两个点到原点的距离,然后相减,便可以得到这两个点的距离。
那么我们如何得到某个点到原点的距离呢?不妨看看某个点到原点的折线呈现出怎样有规律的走向。
①一类是等腰直角三角形的斜边,考虑到这些点其实都在直线x + y = s的直线上,由此我们可以得到这类线段长的总和——s*(s - 1)*sqrt(2) / 2.
②还有一类线段尝试非等腰直角三角形的斜边,可以明显的看出,这些斜边是一系列直角边为i和i - 1的斜边。
③最后一段长度,便是相对于x + y = s这条直线上的不同点。可以说,只要是在这条直线上的点,前面的一段折线距离相等的,只需再加上输入点在该直线上多出的那一段距离,便是总距离。
从以上的数理分析不难发现,计算几何的问题中,对于几何图形的规律化的分类非常重要,这将为设计程序实现自动化编程奠定重要的基础,这一点在凸包问题其实就有所体现。
有了这一层的数理分析,编程实现在几何类的问题不是困难的事情,此处要注意sqrt函数的精度问题。
AC代码如下:
#include<stdio.h> #include<math.h> double dis(int x , int y) { double s = x + y; double distance = s * (s - 1) * sqrt(2.0) * 0.5; for(int i = s;i > 0;i--) distance += sqrt(i * i * 1.0 + (i - 1)*(i - 1)); distance += sqrt(2.0) * x; return distance; } int main() { int x1 , y1 , x2 , y2; int t; scanf("%d",&t); while(t--) { scanf("%d%d%d%d",&x1 , &y1 , &x2 , &y2); printf("%.3lf\n",fabs(dis(x1 , y1) - dis(x2 , y2))); } }
再来看一道有关叉积(在笔者的《计算几何及应用——解析几何》这篇文章有关于叉积定义的引出以及相关规律的证明,这不再累述)应用的简单题目。(Problem scoure:hdu2108)
这道题目是逆时针给出一个n边形的n个顶点,然我们判断它的凹凸性。经过上面关于利用叉积判断三个点的相对位置,这里的数理分析就不是难点了。 关于叉积判断三个点的相对位置的结论如下。
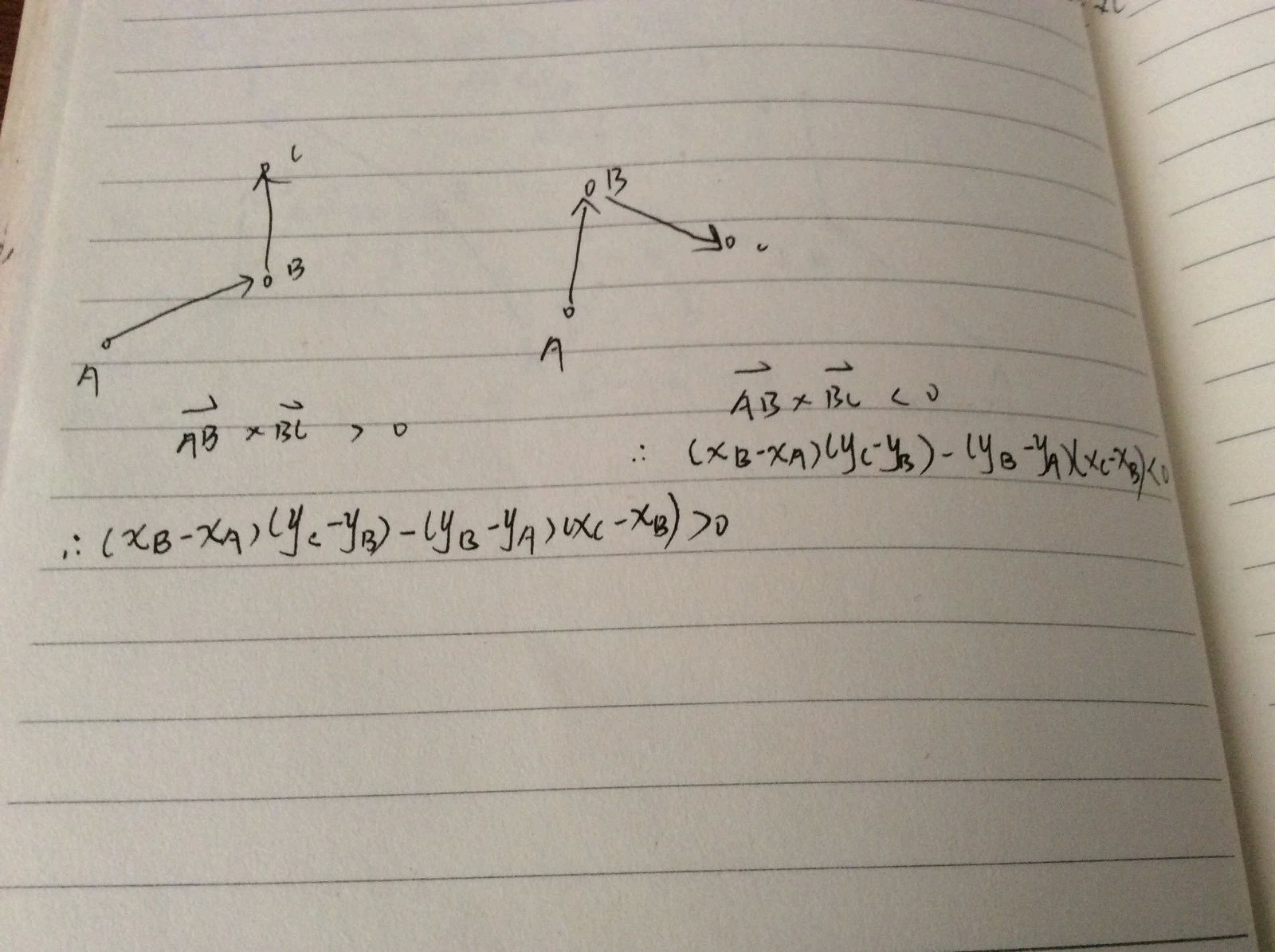
编程实现上,只需遍历的临近的三个点的所有情况,即可。
AC代码如下:
#include<stdio.h> using namespace std; struct point { int x , y; }p[1000]; int Cross_Product(point a , point b , point c) { return (b.x - a.x)*(c.y - b.y) - (b.y - a.y)*(c.x - b.x); } int main() { int n , i; while(scanf("%d",&n) != EOF && n) { for(i = 1;i <= n;i++) scanf("%d %d", &p[i].x , &p[i].y); p[n + 1] = p[1] , p[n + 2] = p[2]; for(i = 3;i <= n + 2;i++) if(Cross_Product(p[i - 2] , p[i - 1] , p[i]) < 0) break; if(i == n + 3) printf("convex\n"); else printf("concave\n"); } return 0; }
我们再来看一道关于叉积的简单题目(Problem source : pku 1106)
Description
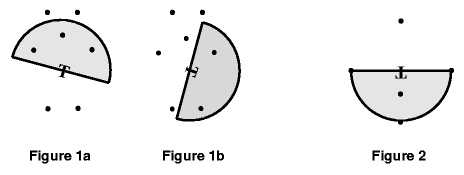
A transmitter T is located somewhere on a 1,000 square meter grid. It broadcasts in a semicircular area of radius r. The transmitter may be rotated any amount, but not moved. Given N points anywhere on the grid, compute the maximum number of points that can be simultaneously reached by the transmitter's signal. Figure 1 shows the same data points with two different transmitter rotations.
Input
Output
题目大意:给点一个半圆的圆心和半径,并给出一个含n个元素的点集,这个半圆可以绕圆心旋转,问你该半圆旋转到一定角度时,能够覆盖到的点的最大数是多少。
数理分析:首先我们当然要在输入的同时找到在整圆覆盖区域内的点,组成一个新的点集,之后我们便需要基于这个新的点集进行穷举查找。
基于这个新点集,进行遍历,我们选出第i个点,表示旋转半圆是的半径过该点,然后再遍历该点集,选出第j个点,判断第j点是否在此时的半圆内,然后进行计数。基于这两层遍历,我们便可以找到落到半圆趋于内点数的最大值。
而问题在于如何判断呢?我们连接点i、圆心o、点j,会发现我们讨论过的叉积会很好的解决这种分析相对位置的问题。
编程实现:通过上文的分析,不难发现整个过程的核心是基础的穷举算法,其中再嵌入叉积的计算公式即可解决问题。
参考代码如下。
#include <stdio.h> #include <iostream> #include <math.h> #include <algorithm> const double eps = 1e-9; using namespace std; struct point { double x , y; }P[155],o,temp; double dis(point a ,point b) { return sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y)); } double crossleft(point a , point b , point c) { return (b.x-a.x)*(c.y-b.y)-(b.y-a.y)*(c.x-b.x); } int main() { double r; int num,i,j; while(scanf("%lf%lf%lf",&o.x,&o.y,&r) != EOF) { if(r <= eps) break; int k = 0; scanf("%d",&num); while(num--) { scanf("%lf%lf",&temp.x,&temp.y); if(dis(temp,o) - r < eps) P[k++] = temp; } int ans , Max = 0; for(i = 0;i < k;i++) { ans = 0; for(j = 0;j < k;j++) { if(crossleft(P[i],o,P[j]) >= 0) ans++; } Max = max(Max , ans); } printf("%d\n",Max); } }
我们再看一道关于点定位的题目。(Problem source:hdu 1756)
题目大意:就是给出n多边形的n个顶点,然后继续输入点坐标,判断此点是否在这个n多边形内部。
数理分析:这是一个很简化的点定位问题,关于点定位问题有多重解法,包括扫描法、叉乘判断法、角度和判断法。这里我们以扫描法为例进行分析,剩下的方法以后将会介绍。
显然n多边形将整个平面分成了三部分:n边形的里面、上面、外面。而我们要判断某个点是否在这个多边形内部,假设我们任意地做了一条以该点为端点的射线,射线无线延伸最终一定是在n多边形的外边,而这条射线在延伸的过程中,与n多边形有一个交点,就意味着这条射线上的点从图形的内部过渡到了图形的外部或者从图形的外部过渡到了图形的内部,那么我们知道,射线上的点最终的归宿是图形的外面,那么过程中如何产生了1个交点,是否意味着起始点位于图形的内部呢?3、5、7个交点是否意味着相同的含义呢。而交点为2、4、6的时候是否恰好相反呢?概括起来,我们得到一个结论:以某点为端点任意做出的射线,如果和n多边形有偶数个交点,那么这个点在n多边形的外面,如果和n多边形有奇数个交点,那么这个点在n多边形的内部。当然,还有一种情况不能少,那便是这个点在n多边形上。
而仅仅知道了这个还是不够的。在实际作图中会出现下面一些特殊的情况。
(1)射线过了某个顶点;(2)射线经过了某个顶点,却没穿过;(3)射线和某个边重合。
那么现在顾及了以上几种特殊情况,我们还要一般情况下的表达式,即解决这样一个问题:如何判断一条射线与一条线段相交?我们不妨画出各种情况。
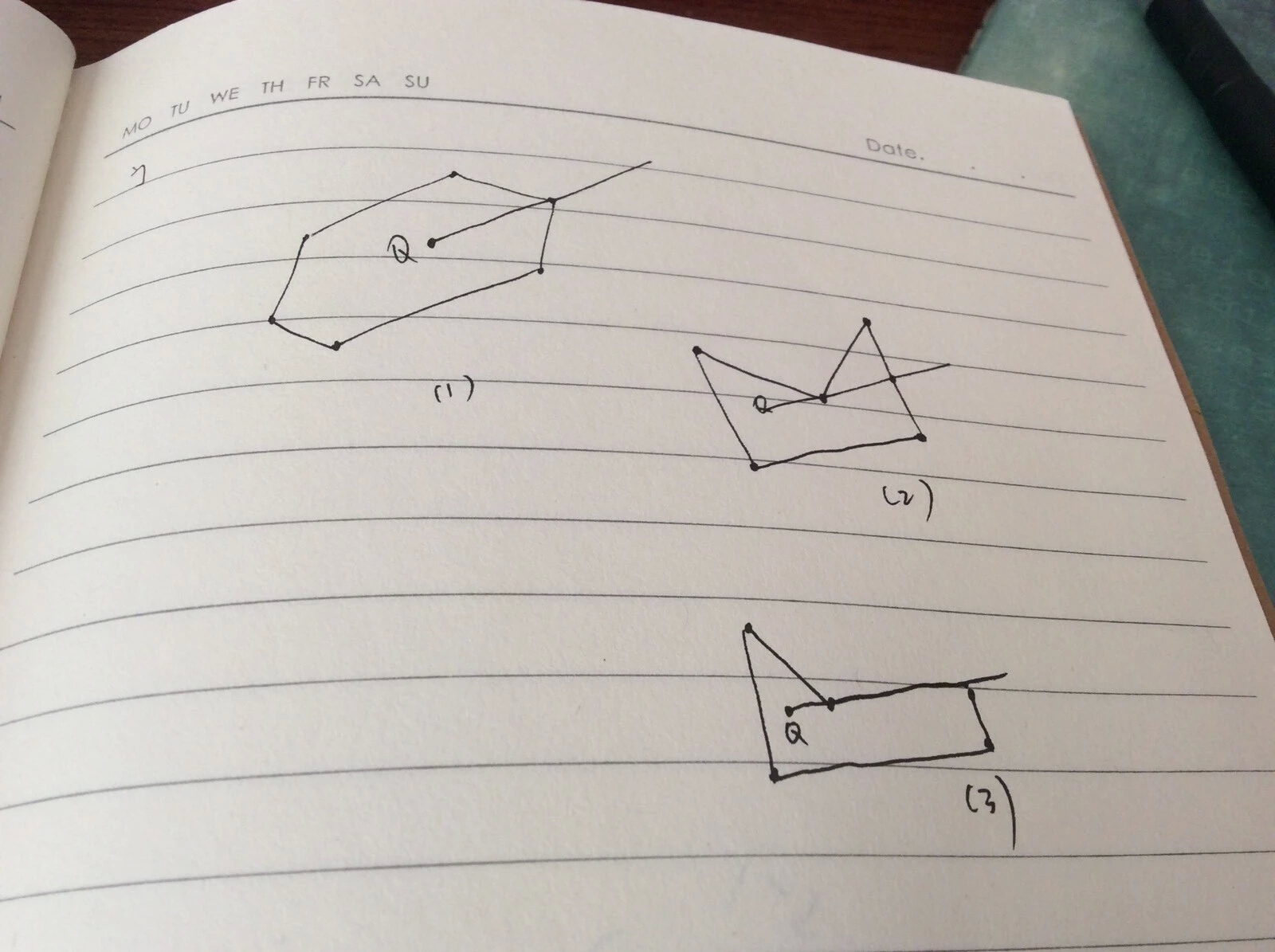
显然(2)是符合要求的情况,那么我们在详细的分析(2)。

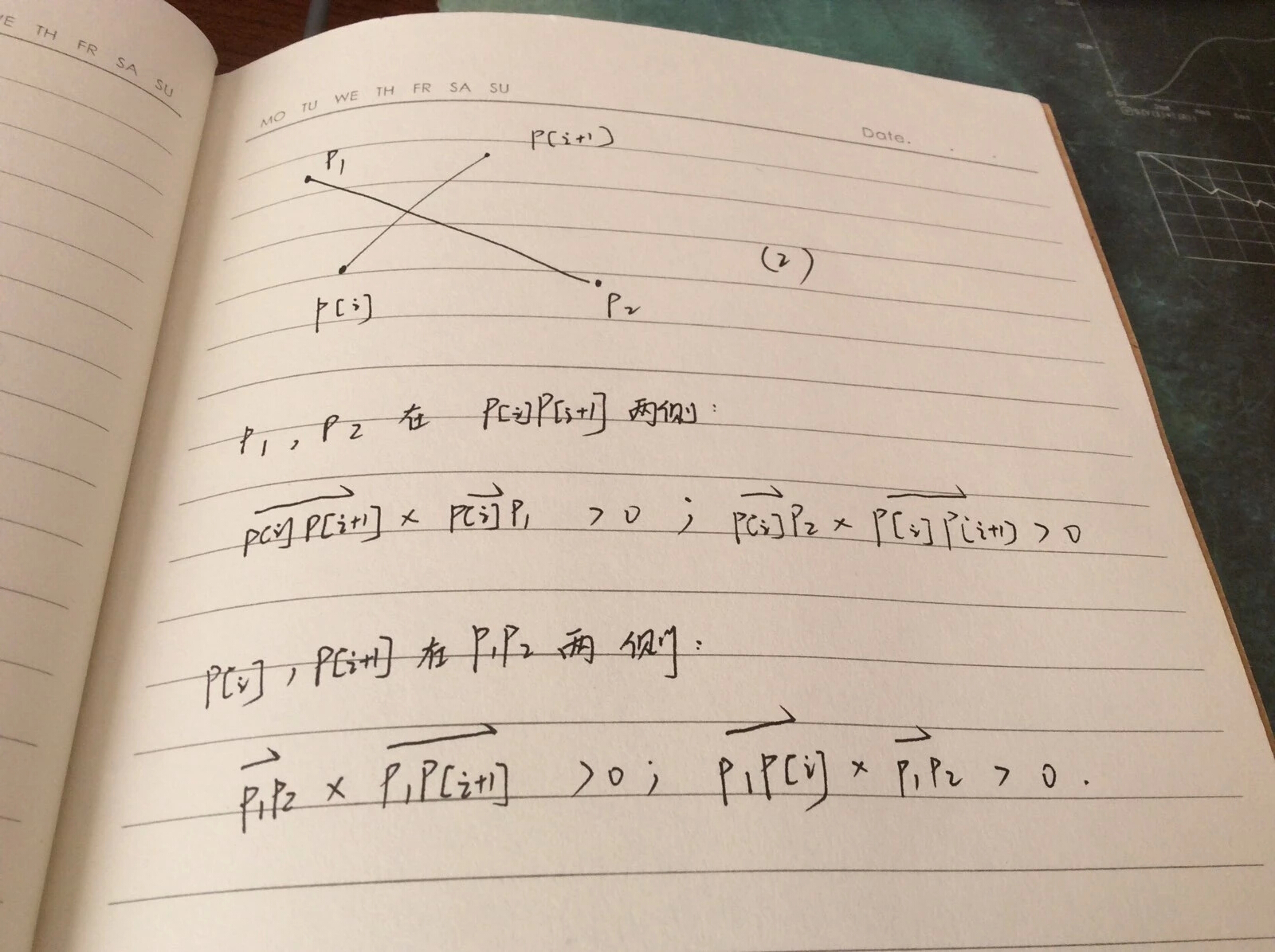
利用叉积这一工具,我们不难找到这几个点在有交点情况下的相对位置,这样我们就得到了可以判断射线和线段是否有交点的的代数表达式了。
接下来便是编程实现了,这里在编程的时候,针对过交点是否记数的问题有两种情况可以讨论,这里我们可以采用“空间换时间”的策略,遇到过交点就弃掉当前构造的射线重新生成,这样牺牲了时间复杂度但是代码相对简洁。
AC代码如下。
#include<stdio.h> #include<stdlib.h> #include<cmath> using namespace std; const double eps = 1e-10; const int offset = 1000; struct point { double x , y; }p[105] , p1 , p2; bool iszero(double x) { return fabs(x) < eps; //double不能与0直接比较 } double Crossleft(point A , point B , point C) //利用叉积判断三点的相对位置 { return (B.x - A.x) * (C.y - A.y) - (B.y - A.y)*(C.x - A.x); } int InPolygon(int n) { int cnt , i = 0; p[n] = p[0]; while(i < n) { p2.x = rand() + offset; //在很远的地方生成一个点构造射线 p2.y = rand() + offset; for(i = cnt = 0 ; i < n ; i++) { if( iszero(Crossleft(p1 , p[i] , p[i + 1])) && //所求点在多边形边上 (p[i].x - p1.x) * (p[i + 1].x - p1.x) < eps && (p[i].y - p1.y) * (p[i + 1].y - p1.y) < eps ) return true; else if(iszero(Crossleft(p1 , p2 , p[i]))) break; //射线过顶点,由于会出现两种情况,这里采取不予分析并重新生成射线 else if(Crossleft(p[i] , p[i + 1] , p1) * Crossleft(p[i] , p2 , p[i + 1]) > eps && Crossleft(p1 , p2 , p[i+1]) * Crossleft(p1 , p[i] , p2) > eps) cnt++; //射线与边相交 } } return cnt & 1; } int main() { int T , n; while(scanf("%d", &n)!= EOF) { for(int i = 0;i < n;i++) scanf("%lf%lf" , &p[i].x , &p[i].y); scanf("%d",&T); while(T--) { scanf("%lf%lf" , &p1.x , &p1.y); if(InPolygon(n)) printf("Yes\n"); else printf("No\n"); } } }
关于线段相交问题。
题目大意:给你n条线段(给你两端点的坐标以确定这条线段),然后让你确定共有多少个不同的交点。
数理分析:显然这里想得到全部的交点个数,我们需要设置穷举,然后一组一组的进行运算看能不能交到一起,那么现在的问题就是,两条已知的线段,你如何计算出二者是否相交。
我们想可以想到他们不相交的情况,通过做图不难发现。

也就是说,一旦满足上面的条件,那么一定是不存在交点的,可以直接进行下一组的判断。 随后我们再思考两线段相交需要满足怎样的条件。 这里通过作图,我们发下,当A、B分别在线段CD的两边,且C、D分别在线段AB的两边的时候,两个线段是相交的。 而既然满足了这种关系,我们再借助向量这一有用的工具,给线段赋予向量的含义,然后再结合向量的叉乘,我们不难得出点坐标之间的代数运算式,于是,线段与线段之间的位置关系,就转化成了线段的端点的点坐标之间的代数关系,这一步重要的转化也为编程的实现做出了奠定了基础。
简略的证明如下(定义向量的方法是不唯一的,因子后面的代数运算式也会呈现出多样性)
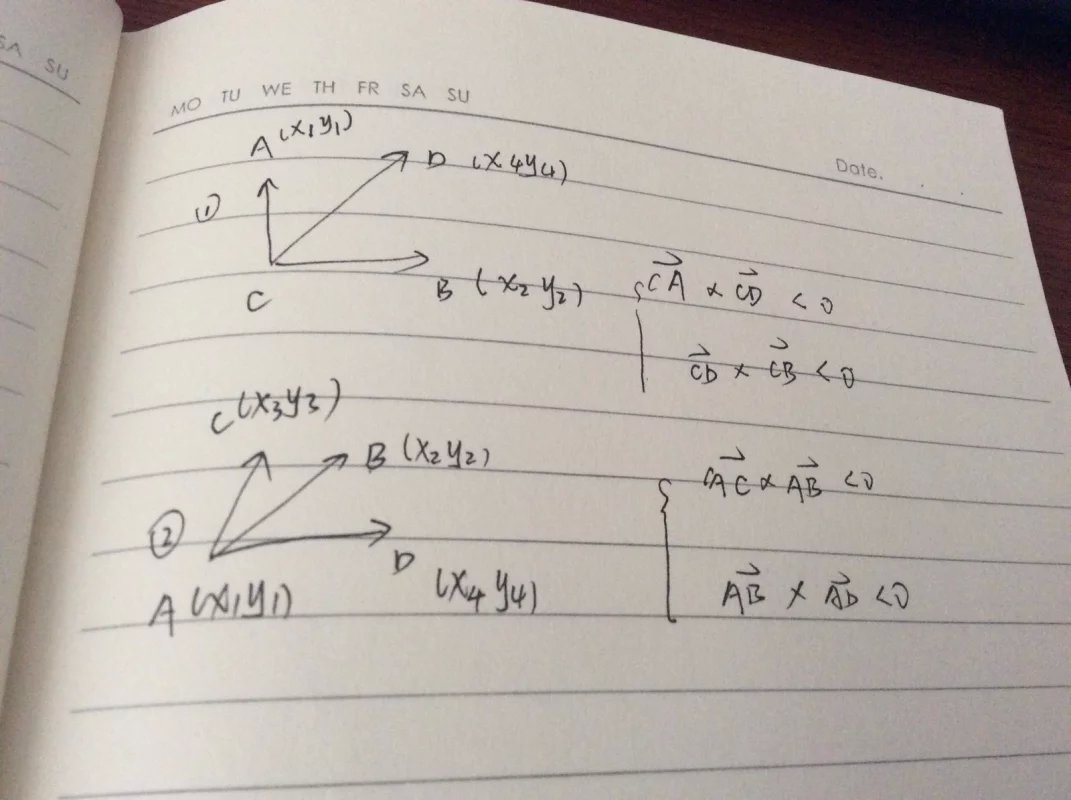
有了以上的数理分析,我们可以写出代码。
#include<stdio.h> #include<math.h> using namespace std; const double eps=1e-10; struct point { double x, y; }; double find_max(double a , double b) { return a > b ? a : b;} double find_min(double a , double b) { return a < b ? a : b;} bool if_intersect(point a ,point b , point c , point d) { if(find_min(a.x , b.x) > find_max(c.x , d.x) || find_min(a.y , b.y) > find_max(c.y , d.y) || find_min(c.x , d.x) > find_max(a.x , b.x) || find_min(c.y ,d.y) > find_max(a.y , b.y)) return 0; double h , i , j , k; h = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x); i = (b.x - a.x) * (d.y - a.y) - (b.y - a.y) * (d.x - a.x); j = (d.x - c.x) * (a.y - c.y) - (d.y - c.y) * (a.x - c.x); k = (d.x - c.x) * (b.y - c.y) - (d.y - c.y) * (b.x - c.x); return h * i <= eps && j * k <= eps; } int main() { point p[105][2]; int i , j , n; while(scanf("%d",&n) != EOF && n) { int sum = 0; for(i = 0;i < n;i++) scanf("%lf%lf%lf%lf", &p[i][0].x, &p[i][0].y, &p[i][1].x, &p[i][1].y); for(i = 0;i < n - 1;i++) for(j = i + 1;j < n;j++) if(if_intersect(p[i][0] , p[i][1] , p[j][0] , p[j][1])) sum++; printf("%d\n",sum); } }
让我们再来看一道关于线段相交的问题。(Problem source :hdu2150)
通过咨询Lele的好友——化学系的TT,Lele决定在田里挖出N条沟渠,每条沟渠输送一种肥料。
每条沟渠可以看作是一条折线,也就是一系列线段首尾连接而成(除了第一条线段开头和最后一条线段的结尾)。由于沟渠很细,你可以忽略掉它的宽度。
由于不同的肥料之间混合会发生化学反应,所以修建的沟渠与沟渠之间不能相交。
现在TT给Lele画了一些设计图,Lele请你判断一下设计图中的沟渠与沟渠之间是否有相交。
题目大意:就是给你还有ki个端点的折线n条,让你判断这些折线是否有交点。
数理分析:既然是判断折线段而且还是多条折线段是否有交点,我们拨开层层迷雾,看到这个大问题的最基元的问题——如何判断两条线段是否有交点。说到这,相信很多读者已经恍然大悟了,因为两条线断,包含着四个点,利用叉积判断其相对位置,我们在上面的一个问题(hdu 1756)中已经讨论过了。而在这里,我们介绍出它原本的学名——跨立实验。
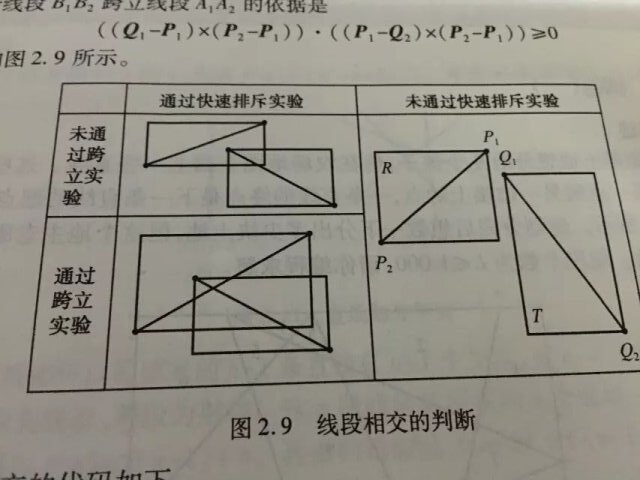
可以看到这里还有一个所谓的快速排斥实验,其实它是基于跨立实验的一步优化,它的计算量小,能够快速在跨立实验之前筛掉一些不相交的情况。(跨立实验笔者在之前的文章也讨论过,不过当时没有引出这个名词)
有了以上的数理思维的铺垫,在编程实现的时候,只需简单的设置多层循环进行端点的穷举遍历即可。
AC代码如下。
#include<stdio.h> #include<algorithm> using namespace std; const int maxn1 = 30 + 5; const int maxn2 = 100 + 5; int s[maxn1]; struct point { double x , y; }p[maxn1][maxn2]; double Crossleft(point A , point B , point C) //叉积表示四点相对位置,也是跨立实验的基础 { return (B.x - A.x)*(C.y - A.y) - (B.y -A.y)*(C.x - A.x); } bool Intersect(point A , point B , point C , point D) { if(max(A.x , B.x) >= min(C.x , D.x) && //快速排斥实验 max(C.x , D.x) >= min(A.x , B.x) && max(A.y , B.y) >= min(C.y , D.y) && max(C.y , D.y) >= min(A.y , B.y) && Crossleft(A , B , C) * Crossleft(A , D , B) >= 0 && Crossleft(C , D , A) * Crossleft(C , B , D) >= 0) //跨立实验 return 1; else return 0; } bool ok(int n) //遍历 { int k1 , k2 , i , j; for(k1 = 1;k1 < n;k1++) for(k2 = k1 + 1;k2 <= n;k2++) for(i = 1;i < s[k1] ; i++) for(j = 1;j < s[k2];j++) if(Intersect(p[k1][i] , p[k1][i+1] , p[k2][j] , p[k2][j+1])) return 1; return 0; } int main() { int n , i , j; while(scanf("%d",&n) != EOF) { for(i = 1;i <= n;i++) { scanf("%d",&s[i]); for(j = 1;j <= s[i] ; j++) scanf("%lf %lf" , &p[i][j].x , &p[i][j].y); } if(n == 1) printf("No\n"); else printf("%s\n" , ok(n) ? "Yes" : "No"); } }
让我们再看一道关于线段相交的问题。(Problem source : hdu 1147)
题目大意:依次n条线段(序号为1~n),然后按照输入的顺序依次往坐标纸上放置该线段,需要你找到所有位于最顶端的线段的序号。
基于这道题目几乎没有数理思维上的难度,我们直接分析它如何用编程来实现。
编程实现:虽然这道题需要用到判断线段相交的算法,但是怎么恰到好处的用也是这道题目的关键。
基于我们要按照输入的顺序放置线段,我们来模拟这个过程。显然我们要开辟一个数组来记录位于顶端的线段。这个过程肯定要和穷举这种基本方法有联系,那么我们就从中间过程分析起,以便我们更加容易的设置循环来实现穷举。
假设我们开的数组f[]来记录顶端的线段,此时我们已经完成了i条线段的放置,那么现在开始放置第i + 1条线段。那么此时我们就需要清空f[],并依次遍历判断f[]中第j条线段是否和第i + 1条线段相交,如果不相交,那么就将这第j个元素再次加入到f[]当中,遍历完成后,还需要将第i条线段加入到f[]当中。这个过程中可能会筛掉f[]中和第i + 1条线段相交的线段,所以我们需要一个新的变量q作为f[]的下标,同时q也是放置第i + 2条线段时遍历f[]数组的一个参量,但是此时我们需要初始化q为0,所以在上一次循环当中,我们用一个中间变量p来记录q的值。
有了上述对求解过程的模拟,我们就可以编程实现了。
参考代码如下。
#include<stdio.h> #include<algorithm> using namespace std; const int maxn = 100001; struct stick { double x1,y1,x2,y2; int No; }f[maxn],e[maxn]; double cross(double x1,double y1,double x2,double y2) { return x1*y2 - x2*y1; } int Find(stick a , stick b) //判断两线段相交,其实满足跨立实验一定会满足快速排斥实验 { double c[4]; //因此为了使代码更加简洁,这里只进行了跨立实验 c[0] = cross(a.x2-a.x1,a.y2-a.y1,b.x1-a.x1,b.y1-a.y1); c[1] = cross(a.x2-a.x1,a.y2-a.y1,b.x2-a.x1,b.y2-a.y1); c[2] = cross(b.x2-b.x1,b.y2-b.y1,a.x1-b.x1,a.y1-b.y1); c[3] = cross(b.x2-b.x1,b.y2-b.y1,a.x2-b.x1,a.y2-b.y1); if(c[0]*c[1] <= 0 && c[2]*c[3] <= 0) return 1; else return 0; } int main() { int n; int i , j , p , q; while(~scanf("%d",&n) , n) { for(i = 0;i < n;i++) { scanf("%lf%lf%lf%lf",&e[i].x1,&e[i].y1,&e[i].x2,&e[i].y2); e[i].No = i + 1; } p = 0; for(i = 0;i < n;i++) { q = 0; for(j = 0;j < p;j++) if(!Find(f[j],e[i])) f[q++] = f[j]; f[q++] = e[i]; p = q; } printf("Top sticks: %d",f[0].No); for(i = 1;i < p;i++) printf(", %d",f[i].No); printf(".\n"); } return 0; }
基于上文介绍的利用快速排斥实验和跨立实验判断两线段是否相交,我们再来看一道类似的问题。(Problem source : pku 3304)
Description
Given n segments in the two dimensional space, write a program, which determines if there exists a line such that after projecting these segments on it, all projected segments have at least one point in common.
Input
Input begins with a number T showing the number of test cases and then, T test cases follow. Each test case begins with a line containing a positive integer n ≤ 100 showing the number of segments. After that, n lines containing four real numbers x1 y1 x2 y2 follow, in which (x1, y1) and (x2, y2) are the coordinates of the two endpoints for one of the segments.
Output
For each test case, your program must output "Yes!", if a line with desired property exists and must output "No!" otherwise. You must assume that two floating point numbers a and b are equal if |a - b| < 10-8.
题目大意:给出n条线段的端点坐标,然你判断是否有一条直线,该直线满足和这n条线段都有交点。
数理分析:这里我们需要将问题进行一定的转化,将当前问题往我们已知的模型上靠拢,这也是G·Polya在《How to solve》一书中给出的关于如何解题的一个核心思想。
我们考虑存在某条直线与n条线段相交的情形,我们观察这条直线与这个线段系的交点中,势必存在两个最靠外围的点,也就是说,整个直线与线段相交的图形,其实可以看成一条直线与两条线段相交,然后这两条线段之间有着线段系中的其他线段,假设上面说的外围的两条线段记作L1、L2,那么L1、L2构成的四边形当中,对角线所在直线是扫过L1、L2之间区域最大的一条直线,也就是说,这条对角线其实是一种临界态,如果这条直线满足要求,那么也许还会有其他满足要求的情况,但是如果这条直线都不满足要求,则说明一定没有直线会满足要求了。(基于以L1、L2为最外层两条线段的情况)
有了这层数理分析,我们看到所谓的对角线,可供我们进行判断的临界状态,其实就是线段端点之间的连线。那么我们枚举出所有端点连线的情况,假设该条线段是符合要求的,然后我们再进行验证——它必须与n条线段都有交点,这便把问题转化成了判断两线段是否相交的问题了。
可能有人会问,我们所枚举的端点连线(还是一条线段)是否需要生成直线呢?因为题设要求的是直线啊。其实根据我们的假设,如果该条线段是符合要求的,那么它就一定是最外层两条线段组成四边形的对角线,显然它与"内部"的其他线段一定是有交点的。
编程实现:有了以上数理分析,我们只需综合判断两线段是否相交的算法、叉乘和穷举所有情况进行判断即可。
参考代码如下。
#include<stdio.h> #include<cmath> using namespace std; const double eps = 1e-9; const int maxn = 105; struct Point {double x ,y;}P[210]; struct Line {Point a , b;}L[110]; double xmult(Point p1 , Point p2 , Point p) { return (p1.x - p.x)*(p2.y - p.y) - (p1.y-p.y)*(p2.x - p.x); } bool segLineInter(Line seg , Line line) //利用叉乘实现的跨立实验 { double d1 , d2; d1 = xmult(seg.a , line.a , line.b); d2 = xmult(seg.b , line.a , line.b); if((d1>eps && d2 < -eps) || (d1<-eps && d2 > eps)) return true; if(fabs(d1) < eps || fabs(d2) < eps) return true; return false; } int main() { int T , n; scanf("%d",&T); while(T--) { scanf("%d",&n); int index = 0; for(int i = 0;i < n;i++) { scanf("%lf%lf%lf%lf",&L[i].a.x,&L[i].a.y,&L[i].b.x,&L[i].b.y); P[index++] = L[i].a; P[index++] = L[i].b; } bool ans = false; for(int i = 0;!ans && i < index ;i++) { for(int j = i + 1;j < index;j++) { bool flag = true; if(fabs(P[i].x - P[j].x) < eps && fabs(P[i].y - P[j].y) < eps) continue;//快速排斥实验 for(int k = 0;k < n;k++) { Line temp; temp.a = P[i]; temp.b = P[j]; if(segLineInter(L[k],temp) == false) { flag = false; break; } } if(flag == true) { ans = true; break; } } } printf("%s!\n",ans ? "Yes" : "No"); } }
我们再来看一道关于线段相交的问题。(Problem source : pku 1066)
Description

Input
Output
题目大意:在一个正方形中,给出n条线段(n道墙),这些线段的特点是端点都在正方形的边上。然后再给出一点(记作A)的坐标,让你计算从A出发,安装多少个门(穿过墙需要在线段的中点建造门),才能走出走出这个正方形。
数理分析:首先,我们对问题进行一步转化。从问题的实际性出发,假设我们已经给出了出口,这个出口和起始点的连线与墙有x个交点(不一定是重点),那表明我们需要造的门也是x个,也就是说,路线(起始点和出口构成的直线)与墙的交点数,等价于需要造的门的数目。通过这一步转化,我们将问题更进一步的往我们已知的判断线段相交的模型上靠拢了。
那么下面的问题是,我们如何得到各种方案以供我们进行比较呢?从A点360°无死角的穷举吗?那显然不太实际。其实我们可以看到,在我们给定的n条线段形成分布在正方形边上的2n个元素的点集,将正方形的外围分割成大大小小的区段,而出口就一定是分布在这些区段里的。假设边上有v1、v2两点(v1、v2中间没有区域点),路线v1A、v1A、viA(vi是线段v1v2上的任意一点)最终的结果是一致的。那么我们就找到了所有的方案,即遍历含有2n个元素的点集,用其中一个元素和起点构成元素数目为n的线段集,然后遍历这个新的线段集的第i个元素,用这条线段去和先前已知条件给出的含n个元素的线段集进行比较,通过判断两条线段是否相交的算法,计算出交点个数,遍历完成之后即可输出焦点数目的最小值。
编程实现:通过以上分析不难看出,这道题目还是利用判断两条线段是否相交的算法和巧妙的穷举算法的相结合。在知道前者的基础上,需要我们去将问题一定程度的转化(路径编程线段、门数目等价于交点数)以便我们设计穷举算法。
参考代码如下。
#include<cstdio> #include<algorithm> using namespace std; const double eps = 1e-9; const long long INF = 9999999999; const int maxn = 31; struct Point{double x, y;}A,B,P[2*maxn],aim; struct Line{Point a , b;}L[maxn]; int n; double xmult(Point p1 , Point p2 , Point p) { return (p1.x-p.x)*(p2.y-p.y) - (p2.x-p.x)*(p1.y-p.y); } bool Intersection(Line u, Line v) { return (max(u.a.x, u.b.x) >= min(v.a.x, v.b.x)) //快速排斥实验 && (max(v.a.x, v.b.x) >= min(u.a.x, u.b.x)) && (max(u.a.y, u.b.y) >= min(v.a.y, v.b.y)) && (max(v.a.y, v.b.y) >= min(u.a.y, u.b.y)) && (xmult(u.a, v.a, u.b)*xmult(u.a, u.b, v.b) > eps) //跨立实验 && (xmult(v.a, u.a, v.b)*xmult(v.a, v.b, u.b) > eps); } void Solve() { scanf("%d", &n); int t = 0; for(int i = 0; i < n; ++i) { scanf("%lf%lf%lf%lf", &A.x, &A.y, &B.x, &B.y); P[t++] = L[i].a = A; P[t++] = L[i].b = B; } scanf("%lf%lf", &aim.x, &aim.y); long long ans = INF; for(int i = 0; i < t; ++i) { int cnt = 0; Line p ; p.a = aim , p.b = P[i]; for(int j = 0; j < n; ++j) { if(Intersection(p, L[j])) { cnt++; } } if(cnt < ans) { ans = cnt; } } printf("Number of doors = %d\n", n?ans+1:1); } int main() { Solve(); }
通过上面几个问题,我们探讨了如何判断两条线段是否相交,那么如果我们想要就求两条线段的交点,该怎么处理呢?
我们直接拿出一个具体的问题来分析。(Problem source : pku 1269)
Description
Input
Output
题目大意:这道题目需要你判断输入的两条线段的关系,有重合、平行、相交三种情况,当出现相交的时候,请计算出交点。
数理分析:我们来依次分析三种情况需要满足的情况。我们设出线段p1p2,p3p4。
1.当两条线断重合:在上文中我们详细的探讨了利用向量的叉积计算来表征三点的相对关系。我们知道,如果向量p1p2与向量p1p3的叉乘的结果为零,则p1、p2、p3共线。 显然,如果p1、p2、p3共线且p1、p2、p4共线,此时两条线段共线。
2.当两条线段平行。基于第一步的判断,我们可以再通过向量p1p2和向量p3p4的叉乘是否为零,如果为零,那么两条线段平行。
3.当两条线段相交,求交点。 在这里我们假设线段p1p2、线段p3p4的交点是p0。那么显然p0、p1、p2共线,p0、p3、p4共线。那么基于这两个条件,我们易得到下列等式。
向量p1p0 x(叉乘) 向量p0p2 = 0
<=> (x0-x1,y0-y1) x (x2-x0,y2-y0)
<=>(y1-y2)x0 + (x2-x1)y0 + x1y2 - x2y1 = 0 ①
类似的我们能得到另一个等式。
(y3-y4)x0 + (x3-x4)y0 + x3y4 - x4y3 = 0 ②
我们会发现①②联立起来是关于x0、y0的二元一次方程组。
我们再基于 a1x + b1y + c1 = 0 ③
a2x + b2y + c2 = 0 ④这个方程组得到带参数的解,然后将①②中的a1、b1、c1等参数带入即可。
基于以上的推导,编程实现上并不困难,参考代码如下。
#include<cstdio>
#include<cmath>
using namespace std;
const double eps = 1e-6;
struct point
{
double x ,y;
};
point p1,p2,p3,p4;
double crossleft(point p1,point p2,point p3)
{
return (p2.x-p1.x)*(p3.y-p1.y) - (p3.x-p1.x)*(p2.y-p1.y);
}
void solve()
{
if(fabs(crossleft(p1,p2,p3)) <= eps && fabs(crossleft(p1,p2,p4)) <= eps)
printf("LINE\n");
else if((p2.x-p1.x)*(p4.y-p3.y) == (p2.y-p1.y)*(p4.x-p3.x))
printf("NONE\n");
else
{
double a1 = p1.y - p2.y;
double b1 = p2.x - p1.x;
double c1 = p1.x*p2.y - p2.x*p1.y;
double a2 = p3.y - p4.y;
double b2 = p4.x - p3.x;
double c2 = p3.x*p4.y - p4.x*p3.y;
double x = (b1*c2 - b2*c1)/(a1*b2 - a2*b1);
double y = (a2*c1 - a1*c2)/(a1*b2 - a2*b1);
printf("POINT %.2lf %.2lf\n",x,y);
}
}
int main()
{
int n;
scanf("%d",&n);
printf("INTERSECTING LINES OUTPUT\n");
while(n--)
{
scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&p1.x,&p1.y,&p2.x,&p2.y,&p3.x,&p3.y,&p4.x,&p4.y);
solve();
}
printf("END OF OUTPUT\n");
return 0;
}
让我们再看一道基础性的计算几何问题。(Problem source : hdu4082)
Problem Description
题目大意:就是给出你n个点,每3个点构成的三角形彼此直线如果相似,那么就归入到一个相似三角形系当中(这里面所有的三角形都彼此相似),那么现在需要你找出这些相似三角形系中含有的最多元素是多少。
数理分析:我们将问题基元话,转化成这样一个小问题——如何判断两个三角形是否相似呢?
由于给出的三角形是关于点的坐标,我们容易将其转化成边长,随后我们容易想到三角形中一条表征边和角关系的定理——余弦定理,利用它和反三角函数,我们能较为简便的得到一个三角形的三个角。那么再判断两个三角形是否相似,就轻松多了。
编程实现:这道题虽然在数理分析上不是很困难,但是编程实现上需要注意的小细节还是很多的。下面是两个比较总要的细节。
①遇到重复出现的点如何处理?(这将为后设置穷举打下铺垫)
②构造的三角形退化成直线如何处理?(显然是剔除掉)
考虑到以上两点编程细节,接下来只需运用基础的编程思想——穷举,来完成所有情况的遍历即可。
参考代码如下。
#include<stdio.h> #include<string.h> #include<math.h> #include <algorithm> using namespace std; const int maxn = 8005; const double eps = 1e-6; struct point { int x , y; bool use; }p[20]; struct Triangle { double ang[3]; }t[maxn]; double dis(point a , point b) { return sqrt((double)(a.x - b.x)*(a.x - b.x) +(a.y - b.y)*(a.y - b.y)); } bool if_triangle(double a , double b , double c) { if(a + b <= c) return 0; else if(a + c <= b) return 0; else if(b + c <= a) return 0; else return 1; } bool ok(Triangle a , Triangle b) { if(fabs(a.ang[0] - b.ang[0]) < eps && fabs(a.ang[1] - b.ang[1]) < eps) return 1; else return 0; } int main() { int flag[maxn] , record[205][205]; int n; double a , b , c; while(scanf("%d" , &n) != EOF && n) { for(int i = 0;i < n;i++) p[i].use = false; memset(record , 0 , sizeof(record)); for(int i = 0;i < n;i++) { scanf("%d %d",&p[i].x , &p[i].y); int tx = p[i].x + 100; int ty = p[i].y + 100; if(!record[tx][ty]) { p[i].use = true; record[tx][ty] = 1; } } int index = 0; for(int i = 0;i < n;i++){ if(!p[i].use) continue; for(int j = i + 1;j < n;j++){ if(!p[j].use) continue; for(int k = j + 1;k < n;k++){ if(!p[k].use) continue; a = dis(p[i],p[k]); b = dis(p[i],p[j]); c = dis(p[j],p[k]); if(if_triangle(a , b , c)) { t[index].ang[0] = acos((a*a + b*b - c*c)/(2*a*b)); t[index].ang[1] = acos((b*b + c*c - a*a)/(2*b*c)); t[index].ang[2] = acos((a*a + c*c - b*b)/(2*a*c)); sort(t[index].ang , t[index].ang + 3); index++; } } } } memset(flag , 0 , sizeof(flag)); int Max = 0; for(int i = 0;i < index;i++) { if(flag[i]) continue; flag[i] = 1; int temp = 0; for(int j = i ;j < index;j++) { if(ok(t[i] , t[j])) { flag[j] = 1; temp++; if(temp > Max) Max = temp; } } } printf("%d\n",Max); } }
我们再来看一道关于圆的基础计算几何题目。(Problem source : hdu1798)
题目大意:分别给出两个圆的圆心坐标和半径,让你求解他们相交部分的面积。
数理分析:很简单的一道数学题,这里运用到最基础的数学分析思维——分类讨论,进行逐一分析即可。
情况1:内切or内含,此时相交面积是小圆的面积。
情况2:外切or相离,此时相交面积是0。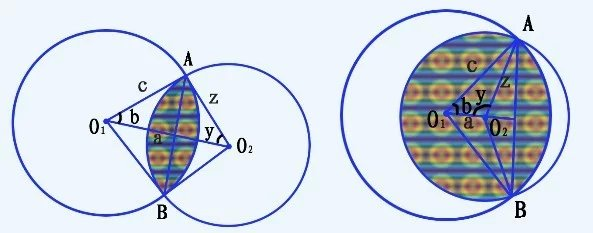
情况3:相交,这里我们表面上看,我们需要考虑俩圆心位于公共弦的同侧和异侧两种情况。那这里我们不妨分别来看一下这两种情况。
①对应左图,s = s扇形(O1AB) - s三角(O1AB) + s扇形(O2AB) - s三角(O2AB)
②对应右图,s = s扇形(O1AB) - s三角(O1AB) + s扇形(O2AB) + s三角(O2AB)。
综合上面两种情况,我们不难发现,其实都可以表示成两个圆对应的扇形趋于减去两个圆心和两个公共点组成的四边形的面积(ABO1O2)。
这里求四边形的面积,我们通过s三角(AO1O2) + s三角(BO1O2)来间接实现。
编程实现上,对于用到的PI以及一些反三角的计算,直接调用库函数即可。
参考代码如下。
#include<stdio.h> #include<cmath> const double PI = acos(-1.0); using namespace std; int main() { double x1,y1,r1,x2,y2,r2; double b , z; double sector1 , sector2; double dis; while(scanf("%lf%lf%lf",&x1,&y1,&r1) != EOF) { scanf("%lf%lf%lf",&x2,&y2,&r2); dis = sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)); if(r1 + r2 <= dis || r1 == 0 || r2 == 0) printf("0.000\n"); else if(fabs(r1-r2) >= dis) printf("%.3lf\n", r1 < r2 ? PI*r1*r1 : r2*r2*PI); else { double a1 = acos((r1*r1 + dis*dis - r2*r2)/(2*r1*dis)); double a2 = acos((r2*r2 + dis*dis - r1*r1)/(2*r2*dis)); sector1 = a1*r1*r1; sector2 = a2*r2*r2; double tri1 = r1*r1*sin(a1)*cos(a1); double tri2 = r2*r2*sin(a2)*cos(a2); printf("%.3lf\n",sector1+sector2-tri1-tri2); } } }
基于对上文中对求两圆相交面积的模型,我们再来看一道相同的题目。(Problem source : pku 2546)
Description
Input
Output
和上一题是一模一样的题目,给出两个圆的圆心和半径,求解两个圆相交的面积,直接调用上文中的代码即可。
让我们再来看一道有关计算几何的基础题目。(Problem source : hdu 4033)
Problem Description
题目大意:给出某点到n个点的距离,让你判断能否利用这n个点构造出正n边形,并使该点在n多边形内部,可以的话,还需给出正n边形的边长。
数理分析:假设这个正n边形存在,该点也在其内部,我们可将n边形分割成数个三角形,而根据三角形各边关系定理,我们可以确定每个三角形的第三边(即我们要求的边长)的取值范围。然后基于这个范围,我们利用基础的二分查找,那么二分查找的出口是什么呢?即根据什么条件判断当前的查找值就是我们构造出来的正n多边形的边长?很显然,我们还是基于正n多边形分割后的数个三角形,通过余弦定理求出凸多边形的边的对角,当遍历了所有的三角形求出的角的和是360°,则表明能够构造出正n边形。
解决了二分查找出口的问题,我们还要思考二分查找过程中如何移动区间。我们进行判断的是区间[l,r]的中点值mid,那么判断完后,我们如何根据结果移动最终解所在的区间呢?
我们来简单的列几个式子。
angle[i] = acos(temp) ①
temp = (a*a + b*b - mid*mid)/2*a*b ②
sum_of_angle = ∑angle[i] ③
我们可以看到sum_of_angle ∝ angle[i] ∝ acos(temp)
我们再基于acos的图像。
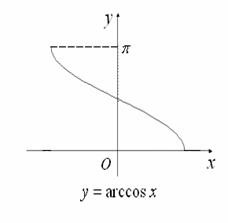
最终我们可以看到。sum_of_angle ∝ mid。因此当sum_of_angle > 2PI时,最终解会落在[l,mid],此时我们需要将mid赋给r。
基于以上的数理分析,我们就可以很好的利用二分搜索的方法来找到最终解了。
参考代码如下。
#include<stdio.h> #include<cmath> #include<algorithm> using namespace std; const int maxn = 105; const double PI = acos(-1.0); const double eps = 1e-10; int main() { int t; int i; scanf("%d",&t); int tt = 1; while(t--) { double dis[maxn]; int n; scanf("%d",&n); for(i = 0;i < n;i++) scanf("%lf",&dis[i]); dis[n] = dis[0]; double l = 0 , r = 20000 , mid; bool flag = 0; for(i = 1;i <= n;i++) { l = max(l,fabs(dis[i] - dis[i-1])); r = min(r,dis[i] + dis[i-1]); } while(r-l>eps) { mid = (l + r)/2.0; double temp , ang , sum = 0; for(i = 1;i <= n;i++) { temp = (dis[i]*dis[i] + dis[i-1]*dis[i-1] - mid*mid)/(2*dis[i]*dis[i-1]); ang = acos(temp); sum += ang; } if(fabs(sum - 2*PI) < eps) { flag = 1; break; } else if(sum > 2*PI) r = mid; else l = mid; } printf("Case %d: ",tt++); if(flag) printf("%.3f\n",mid); else printf("impossible\n"); } return 0; }
我们再来看一道计算几何基础方面的问题。(Problem source : hdu 3902)
Problem Description
题目大意:给出一个n边形的n个顶点坐标,据此判断此n边形是否是轴对称图形。
数理分析:n边形如果是轴对称的,那么必定存在对称轴,我们很容易看到,一个n边形的对称轴要么经过两个顶点,要么经过两个边的中点,那么我们就可以依次遍历给出的点集确定出对称轴,然后判断其是否满足是对称轴的条件即可。
那么一条对称轴需要满足一些什么条件呢?显然,该n边形的剩余顶点应该成对的关于这条对称轴对称,而我们可以通过成对的两点到确定该对称轴的两个点的距离是否相等,来判断成对的点是否关于我们正在遍历的“对称轴”对称。
编程实现:显然我们要设计穷举来完成上面的过程。我们先隔着一个点,给出n个顶点坐标,然后计算出边的中点坐标填充进去,那么我们的点集中就含有2n个点,我们以点集中第i个点作为起点构造对称轴(i∈[1,n],避免了穷举的重复),这条对称轴由第i个点和第i + n个点确定,随后我们再判断点集中剩余点是否关于这条对称轴两两对称即可。
参考代码如下。
#include<cstdio> #include<cmath> using namespace std; const int maxn = 20001; const double eps = 1e-8; int m , n; bool flag; struct node { double x , y; }nodes[2*maxn]; double dis(int i, int j) { double x = nodes[i].x - nodes[j].x; double y = nodes[i].y - nodes[j].y; return sqrt(x*x + y*y); } bool check(int i , int j , int x , int y) { if(fabs(dis(i,x) - dis(j,x)) > eps) return false; else if(fabs(dis(i,y) - dis(j,y)) > eps) return false; else return true; } void sym(int x ,int y) { int i , j; i = j = x; while(1) { i++ , j--; if(j == 0) j = m; if(i == y) { flag = true; return; } if(check(i,j,x,y) == false) return; } } int main() { int i; while(~scanf("%d",&n)) { m = 2*n; for(i = 1;i <= m;i+=2) scanf("%lf%lf",&nodes[i].x,&nodes[i].y); nodes[m+1] = nodes[1]; for(i = 2;i <= m;i+=2) { nodes[i].x = (nodes[i-1].x + nodes[i+1].x)/2.0; nodes[i].y = (nodes[i-1].y + nodes[i+1].y)/2.0; } flag = false; for(i = 1;i <= n;i++) { sym(i,i+n); if(flag) break; } if(flag) printf("YES\n"); else printf("NO\n"); } return 0; }
我们再来看一道很有意思的几何基础问题。(Problem source : pku 1927)
Description
Input
Output
Case i: X
Where i is the case number, and X is the largest area which is rounded to two digits after the decimal point.
题目大意:给出三角形的三边a、b、c,然后给出线段长l,需要你变成计算线段在三角形内部能够圈出最大的面积是多少。
数理分析:从整体的分析思路上来说,我们需要根据l的不同取值来分情况讨论。
在分析之前,我们引入一个经典的等周问题——等周的图形中,圆的面积最大。也可以说成,等周的图形中,该图形越接近圆,其面积越大。它的证明需要一些比较高级的数学方法,这里暂时不详细给出,详情可以查阅相关的数学理论书籍。
情况1:如果l小于该三角形的内切圆的周长,那么只需在三角形内用改线段构造一个小圆即可,一定是最大面积。
情况2:如果l比该三角形的周长还要大的话,那么很显然,能够圈出的最大面积即是三角形的面积。
情况3:l如果介于前两种情况之间,首先给出如下两图进行参考。
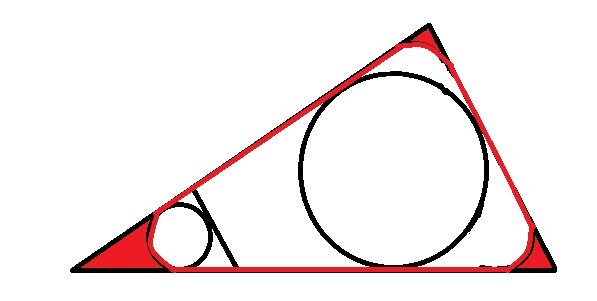
我们容易看到,在这种情况下,圈出的面积包括两部分——直线部分+曲线部分。我们为了圈出更大的面积,尽力使绳子往外张(此处的绳子不具有弹性),然后再基于我们给出的等周问题的结论,我们容易看到曲面部分一定是圆弧,且直线部分和曲线部分的长度是确定的。并且我们又很容易看到,那三部分的圆周的圆心角之和是π,我们固定住直线部分,将这三部分圆弧拼接起来,其实可以看做情况2下的一个子问题,显然应该再圈出一个圆,这其实表明,这三段圆弧的半径是一样的,这个结论将为后面的计算做出重要的铺垫。
基于上面的分析,我们补全任意一个小圆弧,然后如上图所示做出切线,我们就会发现大三角形中的不规则趋于被转移到与之相似的小三角形当中,因此我们就可以得到s = s(大三角) - s(小三角) + s(小三角的内切圆)。
至于怎么求小三角形以及其内切圆的面积,这里就要用到相似三角形和一些合比性质,这涉及一些初级的数学,就不需要详细阐述了。
有了这层数理分析,我们便可以很好的编程实现了。
参考代码如下。
#include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; const double eps=1e-9; const double pi=acos(-1.0); double a, b, c, l; bool cmp(double a , double b) { return a < b ? 1 : 0; } int main() { double len, hl, cosc, area, res, r, k; int tt=1; double edge[3]; while(scanf("%lf%lf%lf%lf", &edge[0], &edge[1], &edge[2], &l) != EOF) { if(fabs(edge[0])<eps && fabs(edge[1])<eps && fabs(edge[2])<eps && fabs(l)<eps) break; sort(edge,edge + 3,cmp); a = edge[0],b = edge[1] , c = edge[2]; len=a+b+c; cosc=(a*a + b*b - c*c)/(2*a*b); if(fabs(cosc)<eps) area=a*b/2 , r=(a+b-c)*0.5; else area=a*b*sqrt(1-cosc*cosc)*0.5, r=area*2.0/len; if(2*pi*r>=l) { r = l/(2*pi); res = pi*r*r; } else if(l>=len) res=area; else { k=(len-l)/(len-2*pi*r); r*=k; res=area-area*k*k+pi*r*r; } printf("Case %d: %.2lf\n", tt++, res); } return 0; }
让我们再来看一道几何方面的基础问题。(Problem source : pku 1380)
Description
Input
Output
题目大意:依次给出两个矩形的边长A,B,x,y,请你判断第二个矩形是否能放入第一个矩形当中。
数理分析:针对两个矩形长和宽之间的不等关系,我们用分类讨论的思想,来分析到这题可以呈现出的所有情况。(这里假定A、x是长,B、y是宽。下文中提及大矩形表示以A、B为边,小矩形则以x、y为边)
情况1:A = x , B = y,能够套入。
情况2:A > x , B > y,能够套入。
情况3:A< x , B < y,不能套入。
情况4:A>x,B<y,这种情况下能否套入就需要分析一下。从一直条件出发,我们从B边处尝试构建一个大于B的边y,针对边y落在不同的位置,我们又可以进行如下的分类讨论。
①y的一个端点在b的端点上,此时显然构造不出套入大矩形中的小矩形。
②y的一个端点在b边中点上端,此时通过相似的知识,我们能够推出y>x,这与初始条件相悖。
③y的一个端点在b边中点下端,此时依然可以通过相似的知识,我们推出y>x,依然与初始条件相悖。
因此我们不难得出结论,B<y时,是无法套入的。
情况5:A<x,B>y,如果重复上面的分析,此时将不会存在与已知条件相悖的情况,因此这种情况下需要我们进一步的讨论。
首先,我们容易看到这种情况下,x、y构成的矩形的对角线是小于b的,因此小矩形的套入存在一种临界状态,就是小矩形的对角线经过大矩形对角线的交点,此时构造出的小矩形是刚好卡入大矩形内部。
因此,如果把小矩形对角线看成变量,每当我们取一个小矩形对角线长度,都会等到一个小矩形的集合,而当小矩形对角线的两个端点在大矩形边上的时候,此时根据均值不等式,x^2 + y^2 = z^2,对于一个集合中的小矩形,z是一个定值,而在这种情况下,能够构造出来的刚好卡入的小矩形是最“方正”的,即x与y较为接近,因此这种刚好卡入的小矩形的周长是这个集合中小矩形的上限,此时这个参数值(最大周长)便可以作为一个判定条件来帮助我们判断当前的小矩形是否能够卡入大矩形。
有了以上数理分析,我们就可以很好的编程实现了,在代码实现中,笔者采用了将小矩形的长和宽正交分解与大矩形的长进行比较,本质上是与上文中的分析是一致的。
参考代码如下。
#include<cmath> #include<stdio.h> void Swap(double &a , double &b) { double t; t = a; a = b; b = t; } bool check(double A ,double B , double x,double y) { if(A < B) Swap(A,B); if(x < y) Swap(x,y); if(A == x && B == y) return true; else if(A < x && B < y) return false; else if(A > x && B < y) return false; else if(A > x && B > y) return true; else { double dis = sqrt(x*x + y*y); double p = asin(B/dis); double q = asin(y/dis); double sina = p - q; double Len = x*cos(sina) + y*sin(sina); if(Len <= A) return true; else return false; } } int main() { double A,B,x,y; int t; scanf("%d",&t); while(t--) { scanf("%lf%lf%lf%lf",&A,&B,&x,&y); if(check(A,B,x,y)) printf("Escape is possible.\n"); else printf("Box cannot be dropped.\n"); } }
我们再来看一道简单的计算几何问题。(Problem source :poj 1473)
Description
You are to write a program that computes the location of and distance to a buried treasure, given a 'traditional' map.
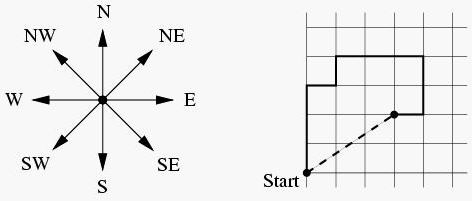
Input
The description is a comma-separated list of pairs of lengths (positive integers less than 1000) and directions (N (north), NE (northeast), E (east), SE (southeast), S (south), SW (southwest), W (west) or NW (northwest)). For example, 3W means 3 steps to the west, and 17NE means 17 steps to the northeast. A full stop (.) terminates the description, which contains no blanks.
Output
On the next line print the distance to that position from the point (0,0), in the format "The distance to the treasure is d.". The fractional values x, y, d must be printed exact to three digits to the right of the decimal point.
题目大意:给你一个字符串,这个字符串涵盖了一些操作步骤,它们以逗号间隔,每个操作单元包括数字+字母,数字表示移动的步数(每一步的长度是单位长度1),字母则表示移动的方向。那么从(0,0)开始,经过这些操作后计算当前的位置以及该位置到原点的距离。
数理分析:读懂了题意之后,发现只需简单模拟即可,设计的编程技巧和几何知识都十分简单。
参考代码如下。
#include <stdio.h> #include <string> #include<math.h> #include<iostream> using namespace std; const double t = sqrt(2.0); int main() { string s; int icase = 1; while(cin >> s) { if(s == "END") { break; } int num = 0; double x = 0, y = 0; for(int i = 0; i < (int)s.length()-1; ++i) { if(s[i] >= '0' && s[i] <= '9') { num = 10*num + (s[i]-'0'); } else if(s[i] == ','){ num = 0; continue; } else if(s[i] == 'N' && s[i+1] == 'E') { x+=num/t, y+=num/t, i++; } else if(s[i] == 'N' && s[i+1] == 'W') { x-=num/t, y+=num/t, i++; } else if(s[i] == 'S' && s[i+1] == 'E') { x+=num/t, y-=num/t, i++; } else if(s[i] == 'S' && s[i+1] == 'W') { x-=num/t, y-=num/t, i++; } else if(s[i] == 'N') { y+=num; } else if(s[i] == 'S') { y-=num; } else if(s[i] == 'E') { x+=num; } else if(s[i] == 'W') { x-=num; } } printf("Map #%d\n", icase++); printf("The treasure is located at (%.3lf,%.3lf).\n", x, y); printf("The distance to the treasure is %.3lf.\n\n", sqrt(x*x+y*y)); } return 0; }