树状数组

　　树状数组的修改和求和都是O(logn)，效率非常高。

　　树状数组——lowbit(x)例如21二进制是10101，1所在的位置是0，2，4，可以分解成2^4 + 2 ^ 2 + ^ 0。进一步的[1,x]可以分解成O(logx)个小区间：

　　1.长度为2^4的小区间[1,2^4]

　　2.长度为2^2的小区间[2^4 + 1,2^4+2^2]

　　3.长度为2^0的小区间[2^4+2^2+1,2^4+2^2+2^0]

　　树状数组如图

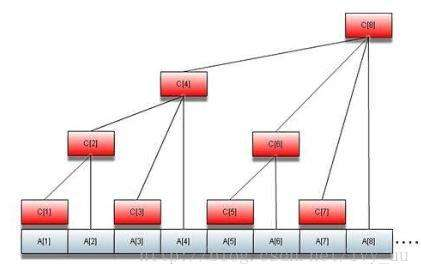
　　C[1] = A[1];

　　C[2] = A[1] + A[2];

　　C[3] = A[3];

　　C[4] = A[1] + A[2]+A[3] + A[4];

　　C[5] = A[5];

　　C[6] = A[6] + A[5];

　　C[7] = A[7];

　　C[8]=A[1] + A[2]+A[3] + A[4]+A[5] + A[6]+A[7] + A[8]

　　树状数组满足以下性质：

　　1.每个内部结点C[x]保存以它为根的子树所有叶节点。

　　2.每个内部结点C[x]的子结点个数等于lowbit(x)的大小。

　　3.除树根外，每个内部结点c[x]的父结点是c[x + lowbit(x)]

　　4.树的深度为O(logn)。

　　一、求lowbit(n)

　　lowbit(n)就是非负整数n在二进制表示下最低位的1以及它后边的0构成的数值。

　　{补码表达式~n = -1-n }因此lowbit(n) = n&(~n+1) = n&(-n)。

1 int lowbit(n)
2 {
3     return n&(-n);
4 }

　　二、对某个元素进行加法操作

　　任意一个结点的祖先至多只有logN个，我们逐一对他们的数组C值进行更新即可。下面的代码在O(logN)时间内执行单点增加操作。

1 void update(int x,int y)
2 {
3     for(i = 1;i <= N;x += x & (-x))
4     {
5         c[x] = c[x] + y;
6     }
7 }

　　三、查询前缀和

　　如本篇开头所写，分成O（logn)个数组，每个数组的区间和都已保存在数组C中，下面的代码在O(logn)的时间内查询前缀和。

 1 int sum(int x)
 2 {
 3     int ans = 0;
 4     while(x > 0)
 5     {
 6         ans = ans + c[x];
 7         x = x - (x & (-x));
 8         return ans;
 9     }
10 }

　　四、统计A[x]……A[y]的值。

　　调用以上的sum的操作：sum(y) - sum(x - 1)

　　五、扩展（多维树状数组）

　　复杂度变成O(logn)^m

　　有一个N*M的二维数组，树状数组是c,那么单点修改操作为：

 1 int update(int x,int y,int z)//将(x,y)的值加上z 
 2 {
 3     int i= x;
 4     while(i <= n)
 5     {
 6         int j = y;
 7         while(j <= m)
 8         {
 9             c[i][j] += z;
10             j += lowbit(j); 
11          } 
12          i += lowbit(i);
13      } 
14 }

 1 int sum(int x,int y)
 2 {
 3     int res = 0,i = x;
 4     while(i > 0)
 5     {
 6         int j = y;
 7         while(j > 0)
 8         {
 9             res = res + c[i][j];
10             j -= lowbit(j);
11         }
12         i -= lowbit(i);
13     }
14     return res;
15 }

　　六、注意事项

　　树状数组的下标不能是0，否则lowbit(0) = 0 ,会陷入死循环中。