我发现写 Solution Set 就不用写每道题的题意了,岂不美哉?
首先是一些奇妙结论。
定理 1(弱周期定理) 对于字符串 \(S\),若 \(S[:p]\) 和 \(S[:q]\) 都是 \(S\) 的周期,且 \(p\not=q,p+q\le|S|\),则 \(S[:\gcd(p,q)]\) 也是 \(S\) 的周期。
证明 考虑更相减损,不妨令 \(q>p\),则只需证 \(S[:q-p]\) 为周期。注意到 \(\forall i\in[1,|S|]\),总有 \(i>p\lor i\le|S|-q\) 成立,对于前者,\(S_i=S_{i-p}=S_{i-p+q}\);对于后者,\(S_i=S_{i+q}=S_{i+q-p}\)。故 \(S[:q-p]\) 为周期。 \(\square\)
这个定理“弱”在 \(p+q\) 的范围,该范围可以扩大到 \(p+q\le|S|+\gcd(p,q)\),在此略过。
定理 2
- 字符串 \(S\) 中所有 \(\ge\frac{|S|}{2}\) 的 border 可排列为一个等差数列。
- 若字符串 \(S\) 的最长 border \(p\ge\frac{|S|}{2}\),则 \(d=n-p\) 是周期;集合 \(B=\{q\in[1,p]\mid q\equiv p\pmod d\}\) 均为 border;且 \([d,p]\) 内的所有 border \(B'\subseteq B\)。(注意区间左端点。)
- 对于字符串 \(S,T\),集合 \(\left\{k\in\left[\frac{|S|}{2},\min\{|S|,|T|\}\right]\mid S[:k]=T[|S|-k+1:]\right\}\) 可排列为一个等差数列。
证明
-
记 \(|S|=n\)。取最大的满足条件的 border \(p\),那么由 定理 1,对于任意满足条件的 border \(q\),有 \((n-p)\mid(n-q)\),且任意满足 \(q\ge\frac{|S|}{2}\land(n-p)\mid(n-q)\) 的 \(q\) 均为 border。因此,可得一个公差为 \(n-p\) 的等差数列。 \(\square\)
-
这是与上一定理形似,但应用更广的扩展。显然 \(d\) 是周期且所有 \(q\in B\) 为 border,我们还需要说明 \([d,p]\) 内不存在其他形式的 border。反证,若存在一个 \(r\in[d,p]\setminus B\) 为 border,则能取出一个 \(q\in B\),使得 \(q,r\) 同属一个周期且 \(|q-r|<d\)。通过说明 \(d'=|q-r|<d\) 也是周期,我们能找到一个大于 \(p\) 的 border,继而导出矛盾。具体讨论见下图:
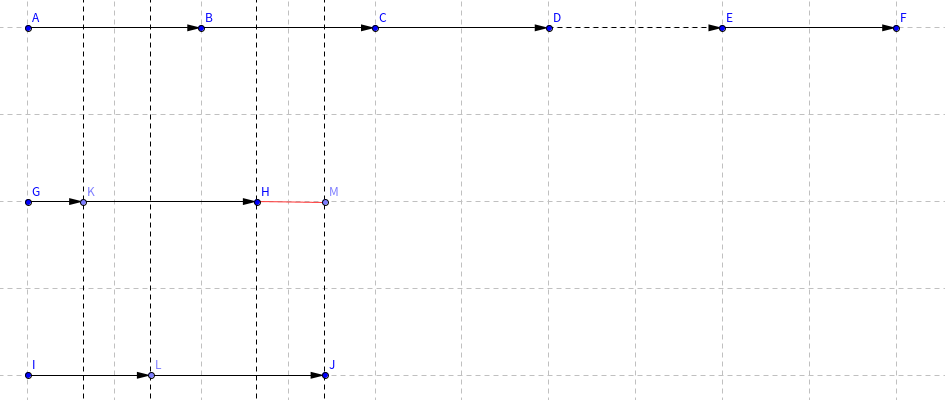
例如 \(r=|GH|,q=|IJ|,d=2\)(网格线单位为 \(1\)),通过在 border 和周期间代换,我们发现在串 \(KM\) 中,\(d\) 是大于半串长的 border,而 \(d'=|HM|\) 便是其周期。继而 \(d=kd'\),所以 \(d'\) 是原串周期。接着上文的讨论,我们导出了矛盾。 \(\square\)
-
类似地,取最大的满足条件的 \(k=p\),那么任意 \(k\) 均为 \(S[:p]\) 的 border,且 \(S[:p]\) 的 border 均满足条件。此后同理可证。 \(\square\)
举一个 定理 2.(1) 的经典使用例子:确保无法均摊复杂度的 KMP(e.g. Trie 上 KMP)复杂度不超过 \(\mathcal O(n\log n)\)。
定理 3 长度为 \(n\) 的字符串 \(S\) 的所有 border 可划分为 \(\mathcal O(\log n)\) 个等差数列。
证明 令 定理 2.(3) 中的 \((S,T)\) 为 \((S,S),(S[:|S|/2],S),(S[:|S|/4],S),\cdots\),分别可证长度在 \([|S|/2,|S|],[|S|/4,|S|/2],\cdots\) 的 border 构成等差序列。由于是复杂度上界我们也没必要考虑边界取不取, 因此得证。此外,我们还能说明,可以按从大到小或从小到大的顺序贪心构造等差数列,这种构造方法能够确保复杂度。 \(\square\)
个人感觉不涉及自动机等模板化算法的字符串题都比较神奇,而 border 又算最神奇的考点,所以相关结论(esp. 定理 3)还是在脑中留个印象比较好√
「洛谷 P5829」「模板」失配树 + 额外限制:空间 \(\le 10\text{ Mib}\)。
不妨记 \(S[:i]\) 的最长 border 为 \(\operatorname{next}(i)\),若没有严格空间限制,显然可以在边 \((\operatorname{next}(i),i)\) 构成的树上求每对 \(p,q\) 的 LCA。
额外的限制要求我们对上文定理的灵活使用。不妨设 \(p>q\),取当前 \(r=\operatorname{next}(p)\),讨论
- \(r<\frac{p}{2}\),可见简单地令 \(p\leftarrow r\) 是可以保障复杂度的;
- \(r\ge\frac{p}{2}\),注意 \(r\) 是 \(S[:p]\) 的最大 border,由 定理 2.(2),若 \(q\equiv r\pmod{p-r}\),则答案为 \(q\);否则令 \(p\leftarrow (r\bmod (p-r))+(p-r)\)。(我们无法保证 \([1,p-r]\) 内无其他形式的 border。)
复杂度显然为 \(\mathcal O(n+m\log n)\),明显于一般的求 LCA 方法(你写四毛子当我没说 w)。
这种匹配计数题一般是用 border 来转移 DP。设 \(l=|S|\),\(B\) 为 \(S\) 的真 border 集合。从暴力入手,令 \(f(i)\) 表示生成了前 \(i\) 个字符,恰好得到一个 \(S\) 的方案数。容斥计数,对于 \(i\ge l\),显然有
第一个和式可以前缀和优化,第二个和式,利用 定理 3 拆分为 \(\mathcal O(\log l)\) 个等差数列上的 \(f\) 之和,亦可前缀和优化。最终复杂度为 \(\mathcal O(n\log l)\)。
询问显然可以视为树形结构,相当于需要在树上 KMP。
发现当两个子串匹配时,它们的二元组表达几乎是一致的,只有左右两端可能不同。所以我们的第一个问题是设计一个基于二元组的 \(\operatorname{next}\) 定义。定义两个二元组串 \(S=(S_1^c,S_1^x)(S_2^c,S_2^x)\cdots\) 和 \(T=(T_1^c,T_1^x)(T_2^c,T_2^x)\cdots\) 有 \(S\approx T\),当且仅当
其实这个 "\(\approx\)" 选得不好,烦请注意 \(\approx\) 没有反身性。此后,对于二元组串 \(S\),定义 \(\operatorname{next}(i)\) 为最大的 \(j\),满足
先不考虑复杂度,这个 \(\operatorname{next}\) 是能够通过正常 KMP 求出来的。接着思考已知 \(\operatorname{next}\) 时如何求最后一个二元组内部的 border 贡献。显然,沿着 \(|S|-1\) 一路跳 \(\operatorname{next}\),维护最后一个二元组已经有多长的前缀找到了 border,考虑当前跳到的位置 \(i\) 的下一个二元组 \(S_{i+1}\) 能否使更长的前缀找到 border,若能,有多长的前缀找到 border,即可计算答案。
现在的唯一问题是复杂度。我们去思考该定义下的 \(\operatorname{next}\) 能否用 定理2.(1) 加速跳跃过程。答案是《能但不完全能》。举个例子
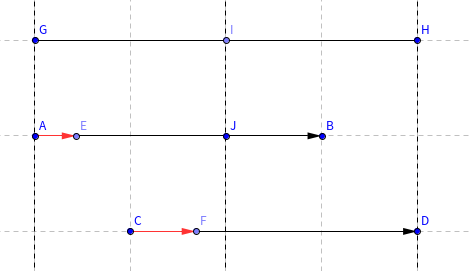
看图,此时 \(S=GH\) 的最长 "border" 为 \(AB\),\(|AB|\ge\frac{|S|}{2}\),\(AB\approx CD\),故第一个二元组 \(|AE|\le|CF|\)。我们只知道,第一个二元组 \(CF\) 在 \(S\) 中点左侧,它无法构成严格等于的周期。因此,我们只能断言通过周期跳跃,着陆在 \(\frac{|S|}{2}\) 之后的某个位置是安全的。当然,这一限制可以收紧,但已经能够保证复杂度。最终复杂度即为 \(\mathcal O(n\log n)\)。
对于竹竿长度 \(x\),初始有 \(x=n\),每次操作可以令 \(x\) 加上 \(n-b\),其中 \(b\) 为 \(S\) 的任意 border,问最终 \([1,W]\) 内有多少可取的 \(x\)。可以发现,这是一个同余最短路模型。
但要小心,如果我们直接开始“优化建图”,很可能忽略原本显而易见的性质。套一般性模板的代价自然是失去特殊性。所以暂时别去想“跑最短路”,只是思考如何求到在某个有意义的模数 \(m\) 下,最小的使得 \(x\equiv r\pmod m,~r=0..m-1\) 的 \(x:=d_m(r)\) 的值。
联系已有结论,感觉等差数列在同余意义下会带来特殊性,所以想到先用 定理 3 拆出等差数列。设 \(x,x+d,\cdots,x+kd\) 均为 \(n-\text{border}\) 的值(注意不是 border 的值),把初始的 \(x\) 作为模数模掉,按照 \(d\) 在模 \(x\) 意义下划分出的 \(\gcd(x,d)\) 个环,用 \(+d,+2d,\cdots,+kd\) 来更新同一个环上的 \(d_x(r)\),注意到边带正权,所以初始最小的 \(d_x(p)\) 不会被更新,可以使用单调队列优化。
然而这种想法导向另一个问题:我们需要实现不同模数下 \(d\) 的转化。考虑 \(d_x(r)\) 的意义:\(d_x(r)+kx~(k\in\mathbb N)\) 都能取到,转化到 \(d_y\) 下,即 \((d_x(r)\bmod y)+k(x\bmod y)~(k\in\mathbb N)\) 都能取到。那么初始有 \(d_y(d_x(r)\bmod y)=d_x(r)\),再用 \(+k(x\bmod y)\) 在 \(d_y\) 之间互相转移。由于 \(k\) 没有上限,不需要单调队列。
综上,我们虽然用同余最短路描述了问题,但仍紧贴 border 的性质完成转化。最终复杂度 \(\mathcal O(Tn\log n)\)。
最重要的结论:字符串题多画图√