01背包问题是动态规划中的经典问题。
本篇文章主题:分析与优化最基本的01背包问题,对此类问题解题有一个基本的解题模板。
问题概述:
有一个背包,他的容量为C(Capacity)。现在有n种不同的物品编号分别为0、1....n-1。其中每一件物品的重量为w(i),价值为v(i)。问可以向这个背包中放入哪些物品,使得在不超过背包容量的基础上,背包内物品价值最大。
思路:
1.暴力法。
每一件物品都可以放进背包,也可以不放进背包。找出所有可能组合一共2^n种组合
时间复杂度:O((2^n)*n)
2.动态规划法。
我们首先使用递归函数自上而下进行思考。
明确两点:
第一、递归函数的定义
第二、数据结构
函数定义:
F(n,C)递归函数定义:将n个物品放入容量为C的背包,使得价值最大。
这里要注意一下,第二个参数一定是剩余容量。我们通过使用剩余容量来控制价值。
F(i,c) = F(i-1,c)
= v(i) + F(i-1 , c-w(i))
状态转移方程:
F(i,c) = max( F(i-1 , c) , v(i) + F(i-1 , c-w(i) ) )
即,当前价值的最大值为,不放入第i个物品(对应剩余容量为c)和放入第i个物品(对应剩余容量为C-w(i))两种情况的最大值。
数据结构:
借某盗版视频中的一个例子:

我们这里选择一个二维数组,来迭代记录处理的结果。
这个二维数组dp[n][C] 其中n为物品数量,C为最大容量。
储存的值dp[i][j]含义为:考虑放入0~i 这些物品, 背包容量为j

我们考虑放入第一个物品。
由于第一个物品,编号为0,重量为1,价值为2。
对于容量为0的背包,放不下该物品,所以该背包价值为0.
其余容量1~5,均可放下该物品。所以只考虑物品0,不同背包大小对应的最大可能价值如图。
第一行处理为初始化,从第二行开始进行迭代。
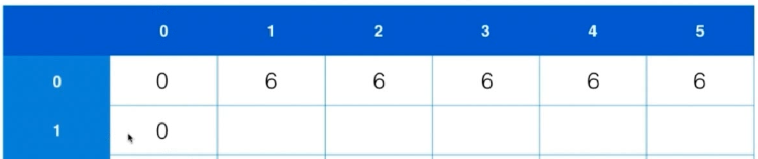
第二行开始,就需要单独处理。
考虑dp[1][0],背包容量为0,理所应当为0
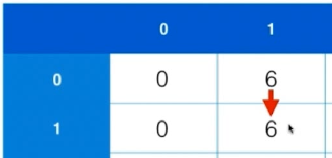
考虑dp[1][1],此处我们依旧无法放入物品1,所以我们使用上一层的结果,即0~0物品在容量为1背包情况的最大价值。
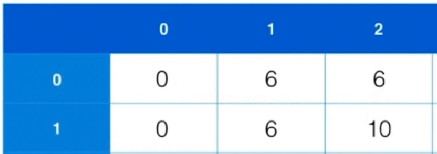
考虑dp[1][2],此处我们终于可以放下物品1了,所以我们考虑如果要放下物品1,剩余背包最大的可能价值,即dp[0][0]
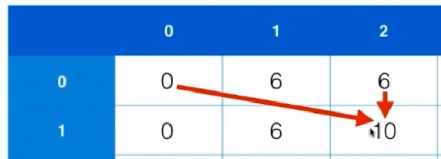
我们对比上一层的情况,以及掏空背包放入物品2的情况。发现最大值为后者,所以dp[1][2]为10
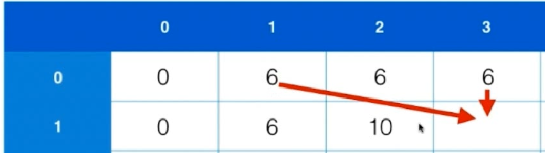
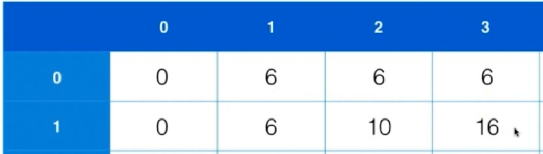
同上,我们掏出可以放下物品1的空间,考虑此时最大价值,即dp[0][1]。对比他和上一层dp[0][3]的大小,发现前者大。
故此时dp[1][3]为dp[0][1]+v[1] = 16.

以此类推,我们每次清空对应物品大小的背包,然后放入对应物品,对比不放入物品的上一行。求出最大值
依次填入dp[][]得出最终的二维数组。
代码如下
class Knapasack01{ public : int knapsack01(int[] w,int[] v,int C){ //w为0-~n-1物品对应价值 //v为0~n-1物品对应重量。 //C为背包容量 int n = w.length(); if(n == 0) return 0; //动态规划记忆数组。 int[][] dp = new int[n][C]; //初始化第一行。 for(int j=0 ; i<= C ; j++) dp[0][j] = (j>=w[0]?v[0]:0); for(int i=1 ; i<n ; i++) for(int j=0 ; j<C ; j++){ dp[i][j] = dp[i-1][j]; if(j>=w[i]) memo[i][j] = (int)Math.max(dp[i][j] , v[i]+dp[i][j-w[i]]); } return dp[n-1][C]; } }