听名字非常的厉害了,它是线段树的高级应用.
考虑如果你需要很多很多线段树的话,你需要开很多很多空间.但是如果这些线段树之间非常相似,我们可以把这一个线段树和上一个线段树共用大部分的节点.
比如一个对与一个数组建立主席树,一个个的把元素放进线段树的话当然可以把重新做一个线段树,但每次只有logn个节点遭到更新或者新建,可以考虑如何压缩空间.
嗯我只理解到了这里,以后继续更新
先用三行离散化一下,处理出总的大小不同的数的数量sum
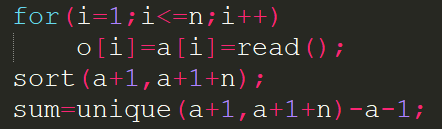
o是原数组,a是用来离散化的.sort一下后a固然会变成有序的,但是unique这句话出来把a内从a[1]到a[n]值不同的数量赋值给sum外还会把这些数值不同的数挑一个放到前面,后面放的不知道是啥.这样子每次查找一个数是第几大的话就可以直接写 k=lower_bound(a+1,a+1+sum,要查的数)-a-1;
然后先用tot++新建节点的方式新建一个树,没有要维护的信息,只是先把左右节点弄一下.设rt[]为最大的根节点的位置,lc[]为左端点,rc[]为右端点,ll[]表示管得到的最小的数(对应离散化之后的数),rr[]表示管得到的最小的数.这里举个栗子:
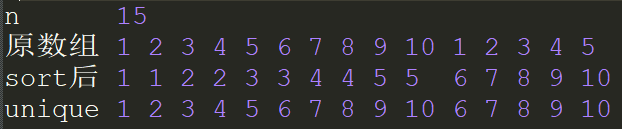
对于n=15的这个数组,显然只有十个本质不同的树.拿他来建树的话就是这样的一个结构:
(哎呀这个紫色也太好看了)
而普通(正常)的线段树
如果把树画出来其实可以发现是一个dfs序,这是和普通的线段树不一样的地方.虽然看起来少了一些点,但是它要多开两个数组记录儿子节点的位置,但普通线段树左右儿子一定是now*2与now*2+1所以不用记录,也不知道谁比较好.但是这个时候比没啥必要,人家主席树还要logn的空间记录以后的信息了.
纪念一下调试代码:

int i; int a[10000],n,m; int tot,rt[100],lc[100],rc[100],ll[100],rr[100]; //rt=root lc左儿子 rc右耳子 void build(int &t,int l,int r){ t=++tot; ll[t]=l; rr[t]=r; if(l==r){ ll[t]=l; rr[t]=r; return ; } int mid=(l+r)/2; build(lc[t],l,mid); build(rc[t],mid+1,r); return ; } void put(int hh){ if(hh/10) cout<<hh; else cout<<' '<<hh; cout<<' ' ; return ; } int main(){ freopen("123.in","r",stdin); freopen("123.out","w",stdout); n=read(); for(i=1;i<=n;i++) a[i]=read(); sort(a+1,a+1+n); int sum=unique(a+1,a+1+n)-a-1; cout<<sum<<endl; build(rt[0],1,sum); cout<<"rt "; for(i=0;i<=sum;i++) put(rt[i]); cout<<endl; cout<<"下标"; for(i=0;i<=tot;i++) put(i); cout<<endl; cout<<"lc "; for(i=0;i<=tot;i++) put(lc[i]); cout<<endl; cout<<"rc "; for(i=0;i<=tot;i++) put(rc[i]); cout<<endl; cout<<"ll "; for(i=0;i<=tot;i++) put(ll[i]); cout<<endl; cout<<"rr "; for(i=0;i<=tot;i++) put(rr[i]); return 0; }
然后考虑把各个数插入线段树并形成新的版本.和单点修改一样,它也只改变logn次即管自己的那几个节点,我们可以把新的节点记录一下,从新的根节点出发,一定先新建一个节点,把自己的管的范围内的数的数量sum++,如果插入的数归左儿子管就去更新左儿子,否则去更新右儿子.如何更新呢?这是一个递归的过程:把这个儿子复制成一个新节点,更新sum与左右儿子. 

每个点被logn个点管着,时间复杂度是n*logn,每次新增logn个点,空间多了一倍而已.
然后就是查询如何做了.查询区间第k大的本质仍是查询区间内区间数的数量,又是一个递归的过程.
考虑区间[1,y]的[l,r]查询就与正常的线段树查询一样,只不过进去的时候由根节点=1变为rt[y].查询[x,y]的话就需要用一下小小容斥[1,y][l,r]-[1,x-1][l,r].然后怎么查第k大呢?考虑同时查看两个地方.整个的主席树等价于n个线段树,每个线段树维护的是只有[1,i]这个范围的数时区间[l,r]的sum.要查询根节点为x,y的第k大(这是两个线段树),对于当前的区间[l,r]可以求出sum[l,mid],如果它大于k说明第k小应该在区间[l,r]里,我们递归进入lc[x],lc[y]管这的子树中,他们管的区间是[l,mid],继续查找第k大;否则应该去rc[x],rc[y]子树中,查找[mid+1,r]中的k-sum[l,mid]大值.最后当l==r时返回下标,它是在离散化数组中的位置.
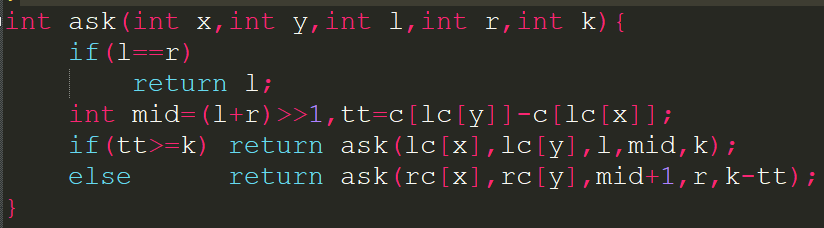

最后给出总的代码.

int i,tx,ty,k; int a[200010],o[200010]; int rt[200010],lc[200010<<5],rc[200010<<5],c[200010<<5],tot; int n,m,sum; void build(int &now,int l,int r){ tot++; now=tot; if(l==r) return ; int mid=(l+r)>>1; build(lc[now],l,mid); build(rc[now],mid+1,r); return ; } int built(int now,int l,int r){ int t=++tot; lc[t]=lc[now];rc[t]=rc[now];c[t]=c[now]+1; if(l==r) return t; int mid=(l+r)>>1; if(k<=mid)lc[t]=built(lc[t],l,mid); else rc[t]=built(rc[t],mid+1,r); return t; } int ask(int x,int y,int l,int r,int k){ if(l==r) return l; int mid=(l+r)>>1,tt=c[lc[y]]-c[lc[x]]; if(tt>=k) return ask(lc[x],lc[y],l,mid,k); else return ask(rc[x],rc[y],mid+1,r,k-tt); } int main(){ n=read();m=read(); for(i=1;i<=n;i++) a[i]=o[i]=read(); sort(a+1,a+1+n); sum=unique(a+1,a+1+n)-a-1; build(rt[0],1,sum); for(i=1;i<=n;i++){ k=lower_bound(a+1,a+1+sum,o[i])-a; rt[i]=built(rt[i-1],1,sum); } for(;m;m--){ tx=read();ty=read();k=read(); write(a[ask(rt[tx-1],rt[ty],1,sum,k)]); putchar(10); } return 0; }
