背景
我!终于学会孙子定理了!!!!!!!!!!!!!!!!!!!!!!!!!!!
好难啊!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
QAQ
中国剩余定理
中国剩余定理又名孙子定理。
在了解中国剩余定理之前,我先放出之前终止了我很长时间的懵逼的一段话。
中国剩余定理介绍
在《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二(除以3余2),五五数之剩三(除以5余3),七七数之剩二(除以7余2),问物几何?”这个问题称为“孙子问题”,该问题的一般解法国际上称为“中国剩余定理”。
在《孙子歌诀》中给出了解决这个问题的解法:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知。很是朗朗上口,但这是什么意思呢?
具体解法分三步:
找出三个数:
1.从3和5的公倍数中找出被7除余1的最小数15,从3和7的公倍数中找出被5除余1 的最小数21,最后从5和7的公倍数中找出除3余1的最小数70。
2.用15乘以2(2为最终结果除以7的余数),用21乘以3(3为最终结果除以5的余数),同理,用70乘以2(2为最终结果除以3的余数),然后把三个乘积相加(15*2+21*3+70*2)得到和233。
3.用233除以3,5,7三个数的最小公倍数105,得到余数23,即233%105=23。这个余数23就是符合条件的最小数。
就这么简单。我们在感叹神奇的同时不禁想知道古人是如何想到这个方法的,有什么基本的数学依据吗?
这是我在看一篇博客的时候,博主写在最前面的一段话。
很多情况下,我们会看不懂博客最大的原因就是,没有强大的知识储备去理解太过空洞的数学推导。
那么这个时候就需要出现一篇充满了友好的例子的博客。【并不指我,是这个
然后在了解什么是孙子之前【雾,我们先了解一个有关的知识
好的我默认你们已经懂了。
接下来切入正题。
我们将“孙子问题”拆分成几个简单的小问题,从零开始,试图揣测古人是如何推导出这个解法的。
首先,我们假设n1是满足除以3余2的一个数,比如2,5,8等等,也就是满足3*k+2(k>=0)的一个任意数。同样,我们假设n2是满足除以5余3的一个数,n3是满足除以7余2的一个数。
有了前面的假设,我们先从n1这个角度出发,已知n1满足除以3余2,能不能使得 n1+n2 的和仍然满足除以3余2?进而使得n1+n2+n3的和仍然满足除以3余2?
这就牵涉到一个最基本数学定理,如果有a%b=c,则有(a+kb)%b=c(k为非零整数),换句话说,如果一个除法运算的余数为c,那么被除数与k倍的除数相加(或相减)的和(差)再与除数相除,余数不变。这个是很好证明的。
我们很显然可以得到下面的三条结论:
- 当n1+n2+n3的和满足除以3余2,n2和n3是3的倍数。
- 当n1+n2+n3的和满足除以5余3,n1和n3是5的倍数。
- 当n1+n2+n3的和满足除以7余2,n1和n2是7的倍数。
孙子问题解法的本质是从5和7的公倍数中找一个除以3余2的数n1,从3和7的公倍数中找一个除以5余3的数n2,从3和5的公倍数中找一个除以7余2的数n3,再将三个数相加得到解。在求n1,n2,n3时又用了一个小技巧,以n1为例,并非从5和7的公倍数中直接找一个除以3余2的数,而是先找一个除以3余1的数,再乘以2.
但是我们要清楚,这个时候我们得到的解并不是最小解。
那么怎么才能得到最小解呢?
我们需要了解一个结论:
如果a%b=c,那么(a*k)%b=a%b+a%b+…+a%b=c+c+…+c=kc(k>0)。
即如果一个除法的余数为c,那么被除数的k倍与除数相除的余数为kc。
所以(n1+n2+n3)%105-->3,5,7的公倍数 就是最终的最小解。
好的,那么我们接下来把它转换成数学语言。
求解同余方程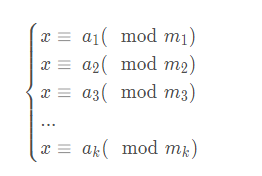
其中m1,m2,..........,mk都是互质的整数,求x的最小非负整数解。
????这都是什么鬼东西????
假设 
那么我们就可以将上面的方程理解为:这个同余方程组 在模N的意义下有唯一解。
如何证明?【图片来自官方博客

什么鬼东西????【切换博客ing...

菜鸡不配学OI系列。。。
经过一个小时的艰苦奋斗,我get到了一篇举例证明的博客。证明一个定理对于蒟蒻来说其实没必要太严谨QAQ
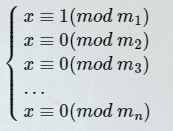
首先,假设 x = (N / m1) *y
那么这个方程就等价于 ( N / m1 ) * y ≡ 1 (mod m1)
即为 ( N / mi ) * yi ≡ 1 ( mod mi )
同理,假设 xi = ( N / mi ) * yi , 就可以构造出原来的方程组(余数为ai)在模N意义下的唯一解:
x = ∑ ai * xi
剩下的不互质 的数怎么处理呢?
详见excrt QAQ。
只要假设 x = ( N / m1 ) ∗ y
那么这个方程就等价于求解 ( N / m1 ) ∗ y ≡ 1 (mod m1)
类比一下就会得到 ( N / mi ) ∗ yi ≡ 1 (mod mi)
同样的,假设 xi = ( N / mi ) ∗ yi ,就可以构造出原来的方程组(余数为ai的方程组)在模N意义下的唯一解:
x=∑ ai·xi
说完了互质的就不由的想到了:不互质的怎么办?
那是excrt,之后有时间再说吧。
练习
luogu P1495 曹冲养猪