前言:
设 $vis_i$ 表示第 $i$ 个点是否更新过其他点;
设 $dis_i$ 表示从起点 $s$ 到达第 $i$ 个点的最短距离;
设 $sdis_i$ 表示从起点 $s$ 到达第 $i$ 个点的严格次短距离;
设 $dis(u,$ $v)$ 表示第 $u$ 个点到达第 $v$ 个点的距离;
最短路:
题目link:https://www.luogu.com.cn/problem/P4779
Part1:
$ ext{Dijkstra}$ 的 $O(n^2)$ 做法:
$ ext{Dijkstra}$ 的思想是每次找到一个 $dis$ 值最小的并且 $vis$ 值为 $ ext{false}$ 的一个点 $i$,并用 $i$ 去更新其他点的 $dis$。
容易发现这是一个贪心的思想,并且很容易证明一个点更新完其他点后,它的 $dis$ 值一定不会再重复被更新(它的 $dis$ 值已经是没更新过其他点的点中最小的了,也就不可能再被那些点更新了)。
Part1.1:
那么这样便可以得出 $ ext{Dijkstra}$ 的代码:
1 int head[MAXN + 10], dis[MAXN + 10]; 2 bool vis[MAXN + 10]; 3 4 struct Node { 5 int nxt, to, val; 6 }stu[2 * MAXM + 10]; 7 8 void dijkstra(int s) { 9 10 std::memset(dis, 0x3f, sizeof(dis)); 11 std::memset(vis, false, sizeof(vis)); 12 13 dis[s] = 0; 14 int cur; 15 for(int k = 1; k <= n; ++k) { 16 int mindis = INF; 17 for(int i = 1; i <= n; ++i) { 18 if(dis[i] < mindis && !vis[i]) { 19 mindis = dis[i]; 20 cur = i; 21 } 22 } 23 vis[cur] = true; 24 for(int i = head[cur]; i; i = stu[i].nxt) { 25 int v = stu[i].to; 26 dis[v] = std::min(dis[v], dis[cur] + stu[i].val); 27 } 28 } 29 30 return; 31 }
Part1.2:
但是众所周知,$ ext{Dijkstra}$ 算法无法处理负边权的情况,下面给出证明:
因为 $ ext{Dijkstra}$ 是利用了贪心的思想,可以得出一个点的更新完其他点后不会再被更新这个性质来求出所有点的 $dis$ 值。但是当图上存在负边权的时候,容易发现此时这个性质无法得到保证,因为在 $u$ 更新完 $v$ 后,如果 $dis(u,$ $v)$ 是负值并且这是一条双向边,那么 $v$ 还可以转过头来更新 $u$,这就导致 $ ext{Dijkstra}$ 算法出现错误,故 $ ext{Dijkstra}$ 算法无法处理负边权的情况。
Part2:
$ ext{Dijkstra}$ 的 $O(m$ $log$ $m)$ 做法:
考虑优化前面的 $O(n^2)$ 做法。
可以发现前面的做法需要找到一个 $dis$ 值最小的并且 $vis$ 值为 $ ext{false}$ 的点,那么这里容易想到用一个小根堆去优化它。
每次更新完一个点就把这个点的编号和这个点的 $dis$ 值扔进小根堆里面,可以用一个 $ ext{pair}$ 来存放它们(但是注意:$ ext{pair}$ 是优先按 $ ext{first}$ 来排序,因此要 $dis$ 值在前,编号在后!!!)。
Part2.1:
这时的 $ ext{Dijkstra}$ 算法还是满足一个条件,就是从堆顶拿出的点,它此时的 $dis$ 值一定是最优的,但是与这个点的编号一同存在堆里头的 $dis$ 值不一定是最优的。
这里可以举出一个例子来证明它:
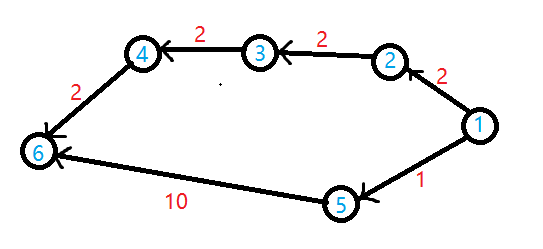
比如说最开始起点放入堆里,更新了 $5$ 号点和 $2$ 号点,之后把 $5$ 号点和 $2$ 号点放进了堆里;
显然此时先是用 $5$ 号点去更新 $6$ 号点,接着 $6$ 号点被放进了堆里(注意:此时 $6$ 号点连着一起放入堆里的 $dis$ 值是 $11$);
此时堆里头有第一次更新的 $2$ 号点和新更新的 $6$ 号点,显然 $2$ 号点先更新其他点,于是 $3$ 号点被更新并放入堆里;
此时堆里有 $6$ 号点和 $3$ 号点,显然 $3$ 号点先更新其他点,于是 $4$ 号点被更新并放入堆里;
此时堆里有 $6$ 号点和 $4$ 号点,显然 $4$ 号点先更新其他点,于是 $6$ 号点又被更新并再次被放入堆里;
那么现在堆里头只剩下两个 $6$ 号点了,那么这个时候就会发现,最先放入堆里的 $6$ 号点的放入堆里的 $dis$ 值并不等于现在 $6$ 号点的 $dis$ 值,但是容易发现此时该 $6$ 号点去更新了(可以假设 $6$ 号点的后面还有其他点),它的 $dis$ 值也已经是最优的了,因此问题得证。
Part2.2:
既然得到这样一个做法了,那么现在再来看一个问题,就是此时的 $vis$ 数组是否还有作用了(也就是说去掉 $vis$ 行不行)。
容易发现,这时一个点能被扔进堆里面的条件是它是否被更新,而这个点它不可能无限次的更新下去因为它的最短路不可能无限的变小,因此一个点就不可能被反复扔进堆里,也就是说不会导致死循环,并且也很容易理解去掉 $vis$ 数组后 $ ext{Dijkstra}$ 算法的正确性,因此为什么不把 $vis$ 数组去掉?
实践出真知,当把去掉 $vis$ 数组的 $ ext{Dijkstra}$ 交上去后可以发现程序 $ ext{TLE}$ 了,那么说明这个 $vis$ 数组和时间复杂度有关系(并且不是死循环导致的)。
容易发现,总共放入堆里的元素的个数可能是 $m$ 级别的,因为每一条边都可能会更新一个点的 $dis$ 值,进而把这个点放入堆里,这里顺便可以得出正常的加上 $vis$ 数组的堆优化 $ ext{Dijkstra}$ 算法的复杂度就是 $O(m$ $log$ $m)$ 的(小根堆带一个 $log$ 的复杂度)。
但是如果不加这个 $vis$ 数组的话,一个点它最多可能会被扔进堆里 $n$ $-$ $1$ 次(即每个点都可以更新它),然后它再枚举一下它所有出边(假设这个点和除自己以外的每个点都有连边), 然后图再构造一下,多来几个这样 “最坏的点”,并把它多扔进堆里几次,可以发现这个复杂度就有可能炸掉了,具体值不说,总之肯定比 $O(m$ $log$ $m)$ 要差远了,这也就证明了 $vis$ 数组的必要性。
Part2.3:
下面给出堆优化过的 $ ext{Dijkstra}$ 的代码:
1 using std::pair; 2 using std::make_pair; 3 4 int head[MAXN + 10], dis[MAXN + 10]; 5 bool vis[MAXN + 10]; 6 7 struct Node { 8 int nxt, to, val; 9 }stu[2 * MAXM + 10]; 10 11 std::priority_queue <pair<int, int>, std::vector<pair<int, int> >, std::greater<pair<int, int> > > q; 12 13 void dijkstra(int s) { 14 15 std::memset(dis, 0x3f, sizeof(dis)); 16 std::memset(vis, false, sizeof(vis)); 17 18 dis[s] = 0; 19 q.push(make_pair(0, s)); 20 while(!q.empty()) { 21 int u = q.top().second; 22 q.pop(); 23 if(!vis[u]) { 24 vis[u] = true; 25 for(int i = head[u]; i; i = stu[i].nxt) { 26 int v = stu[u].to; 27 if(dis[u] + stu[i].val < dis[v]) { 28 dis[v] = dis[u] + stu[i].val; 29 q.push(make_pair(dis[v], v)); 30 } 31 } 32 } 33 } 34 35 return; 36 }
Part3:
例题:佳佳的魔法药水
题目link:https://www.luogu.com.cn/problem/P1875
考虑沿用 $ ext{Dijkstra}$ 的贪心思想。
设 $price_i$ 表示第 $i$ 个药水的价格,那么先将 $price_i$ 全部赋值成初始价格;
每次从所有的药水中找到一个 $price$ 值最小的药水,并用这个药水的所有配方去更新所配出来的药水的价格就行了,如果价格相等整一下方案数就行了。
代码和 $ ext{Dijkstra}$ 相差无几,这里不再给出。
次短路:
题目link:https://www.luogu.com.cn/problem/P2865
求次短路可以在求最短路的同时求出来。
在用 $ ext{Dijkstra}$ 求最短路的时候,设当前点是 $u$,它所指向的一个点是 $v$。
下面分三种情况来讨论:
if(dis[u] + stu[i].val < dis[v]) { sdis[v] = dis[v]; // 最短路更新,次短路变最短路 } if(sdis[u] + stu[i].val < sdis[v]) { sdis[v] = sdis[u] + stu[i].val; // 次短路更新次短路 } if(dis[u] + stu[i].val > dis[v] && dis[u] + stu[i].val < sdis[v]) { sdis[v] = dis[u] + stu[i].val; // 如果最短路无法更新,但可以更新次短路就更新次短路 }
但是这样子就完事了吗?就可以套 $ ext{Dijkstra}$ 算法的模板了吗?并没有。
容易发现它可以被这样一种数据卡掉:
2 1 1 2 3
这样一种数据它的最短路是显然的,但是由于我们设定了 $vis$ 数组,因此每个点只会更新其他点一次,这样虽然最短路正确,但是次短路就无法更新了(正常应该是折返更新)。
当然一种方法就是直接暴力地把 $vis$ 数组去掉,不过这样复杂度显然不是非常正确。
于是得出了第二种做法,就是去掉 $vis$ 数组后再增加一个判断条件,也就是判断和堆里面拿出来的点连着的它的 $dis$ 值和它现在的 $dis$ 值是否相等,如果相等的话就更新,否则不更新。
原因就是,如果一个点满足上述条件,那么只可能时两种情况,一种是它的最短路被更新了,而另一种是它的次短路被更新了,显然两种情况都需要它去更新其他的点,因此此方法正确(之所以设这个条件是因为每个点可能多次进堆里面,因此这样可以避免重复做无用的更新)。
下面给出次短路的代码:
1 using std::pair; 2 using std::make_pair; 3 4 int head[MAXN + 10], dis[MAXN + 10], sdis[MAXN + 10]; 5 6 struct node { 7 int nxt, to, val; 8 }stu[2 * MAXM + 10]; 9 10 std::priority_queue <pair<int, int>, std::vector<pair<int, int> >, std::greater<pair<int, int> > > q; 11 12 void dijkstra(int s) { 13 14 std::memset(dis, 0x3f, sizeof(dis)); 15 std::memset(sdis, 0x3f, sizeof(sdis)); 16 17 q.push(make_pair(0, s)); 18 dis[s] = 0; 19 while(!q.empty()) { 20 int u = q.top().second; 21 int d = q.top().first; 22 q.pop(); 23 if(d == dis[u]) { 24 for(int i = head[u]; i; i = stu[i].nxt) { 25 int v = stu[i].to; 26 int flag = 0; // 判断放进堆里面一次就行了 27 if(dis[u] + stu[i].val < dis[v]) { 28 sdis[v] = dis[v]; 29 dis[v] = dis[u] + stu[i].val; 30 q.push(make_pair(dis[v], v)); 31 flag = 1; 32 } 33 if(sdis[u] + stu[i].val < sdis[v]) { 34 sdis[v] = sdis[u] + stu[i].val; 35 if(!flag) { 36 q.push(make_pair(dis[v], v)); 37 flag = 1; 38 } 39 } 40 if(dis[u] + stu[i].val > dis[v] && dis[u] + stu[i].val < sdis[v]) { 41 sdis[v] = dis[u] + stu[i].val; 42 if(!flag) { 43 q.push(make_pair(dis[v], v)); 44 } 45 } 46 } 47 } 48 } 49 50 return; 51 }