球盒问题的意思是有n个球,m个盒子,问将n个球放入m个盒子有多少种方案数。(n ≥ m)
其中有三个变量,分别是球是否不同、盒子是否不同、盒子是否为空,因此一共有8个问题。
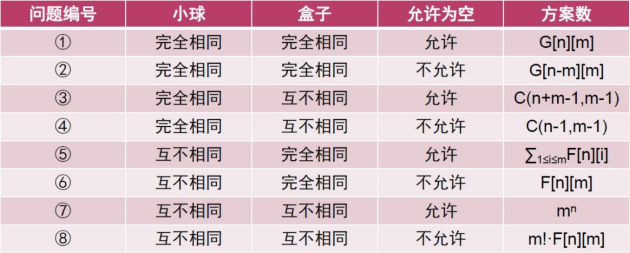
其中
F[i][j] = F[i - 1][j - 1] + F[i - 1][j] * j
G[i][j] = G[i][j - 1] + G[i - j][j]
- 1.球不同,盒子不同,可以为空:
从一个球入手,每个球都可以放入任何一个盒子,因此每个球有m种放球方案,一共有n个球,所以总方案数是mn。
因为每个球不同,盒子不同,所以不会有重复的情况。
- 2.球相同,盒子不同,不可以为空:
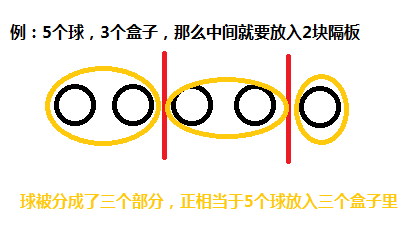
因为球都是相同的,且盒子不同,所以可以使用隔板法来解决这个问题。
考虑将n个球排成一排,中间放入m - 1个隔板(因为盒子不可以为空,所以隔板不能重合且不能放在两边),这样球就被分成了m块,与将n个球放入m个盒子是一样的。
所以总的方案数就被转化成了放隔板的方案数,因为n个球两两之间有n - 1个缝隙,需要插入m - 1个隔板,且隔板之间不能重合,所以总的方案数就是C(n - 1, m - 1)。
- 3. 球相同,盒子相同,可以为空:
这个也可以用隔板法来求,因为盒子可以为空,所以板子可以相邻(及这个盒子为空),同时板子也可以放在两边(也表示这个盒子为空)。
这样又转化为了放隔板的方案数,但用上面那个解法做起来可能有点麻烦,考虑将球和板子看成同一种物体,有n + m - 1个空位,其中n个空位放球,m - 1个空位放板子,那么在这n + m - 1空位中,放m - 1个板子的方案数就是C(n + m - 1, m - 1);
- 4. 球不同,盒子相同,不可以为空:
这个可以用递推来求,设F[i][j]表示用j个盒子来装前i个球的方案数。
考虑第i个球此时的状态,它可以放入一个新的盒子中,因为所有的盒子都是相同的,所以放入任意一个新的盒子方案数都是相同的,那么方案数为F[i - 1][j - 1](表示前i - 1个球放入j - 1个盒子里,然后用第j个盒子(其实用没装过小球的哪个盒子装都一样)来装第i个小球);它也可以放入一个放过球的盒子里,因为球是不同的,所以放入j个盒子中,哪个盒子的方案是不同的,那么方案数就要 * j,及F[i - 1][j] * j(表示前i - 1个球放入j个盒子里,然后第i个小球放入j个盒子中任意一个)。
那么用j个盒子来装前i个球的方案数就是F[i - 1][j - 1] + F[i - 1][j] * j。
转移方程为F[i][j] = F[i - 1][j - 1] + F[i - 1][j] * j。
因为不可以为空,所以最后的答案就是F[n][m]。
- 5. 球不同,盒子相同,可以为空:
与上一个不同的是,盒子可以为空,而其他不变,因此F[i][j]的状态不变,方程转移也不变,只有最后的答案变了。
因为盒子可以为空,所以最终的答案和盒子的数量无关,因此只需要枚举盒子数量,答案累加F[n][i](及将n个球放入i个盒子)即可。
- 6. 球不同,盒子不同,不可以为空:
这个和第4个也是一样的,但是因为这个盒子是不同的,所以最后的答案也会难免增加。
先通过打表发现盒子不同的方案数总是是盒子相同的方案数的 m! 倍,下面证明一下。
对于两个不同的盒子,在盒子相同的基础上,每种方案都可以将两个盒子中的球互换形成一种新的方案,于是盒子不同的方案就是盒子相同的方案的2倍;对于三个不同的盒子,每种方案都可以将第一个盒子中的球与第二个盒子中的球互换,第二个盒子中的球再与第三个盒子中的球互换……以此类推,共有6种互换方式,于是答案就 * 6。像这样,很容易得出是 * m!。
- 7. 球相同,盒子相同,可以为空:
这种情况用考虑第i个的方法做不出来了,于是考虑用一种操作来模拟放球的过程。
设置两个操作:1. 新建一个盒子; 2. 将每个盒子中增加一个球
设G[i][j]表示用j个盒子来装i个球的方案数,易得出转移方程为G[i][j] = G[i][j - 1](新建一个盒子) + G[i - j][j](将每个盒子中放入一个球)。
对于每个盒子,显而易见前面盒子中的球个数一定 ≥ 后面盒子中球的个数的,因此答案不会重复。
对于为什么这个操作与球盒问题的第七个相对应,是因为对于球相同且盒子相同,考虑第i个球,它可以放入一个新的盒子,但放入任何一个盒子的方案数都是相同的;它也可以放入一个有球的盒子里,但是在这个盒子中放入这个球后,这个盒子中的球的数量不能大于之前盒子中的数量,否则就会重复。
因此这个问题也是前面盒子中的球个数一定 ≥ 后面盒子中球的个数的,可以发现它与G数组性质一样,因此它们是一一对应的。
最后的答案就是G[n][m]。
这种做法是凭经验想出来的。
- 8. 球相同,盒子相同,不可以为空:
这个与上一个一样,但因为不可以为空,只需要在每个盒子中事先放入一个球即可。
于是这个答案就是G[n - m][m]。