线段树是修改,查找一组数据比较常用的数据类型,相对树状数组来说,线段树更加灵活,可以完美实现单点和区间的查找与修改,甚至可以做到树状数组做不到的区间赋值修改。
线段树及存值方式
线段树不同于树状数组,线段树是一棵真正的树,它具有左子树和右子树,每一个节点存有一个初始序列一个区间内区间和,且两个子节点所存的区间和之和等于父节点所存的区间和,假设每一个节点的信息如下图所示:

l~r代表此节点存有初始序列区间l~r的区间和;sum即为区间l~r的区间和;k代表节点序号
一个线段树就如下图所示,初始序列nu={1,2,2,3,3,4,4,5}:
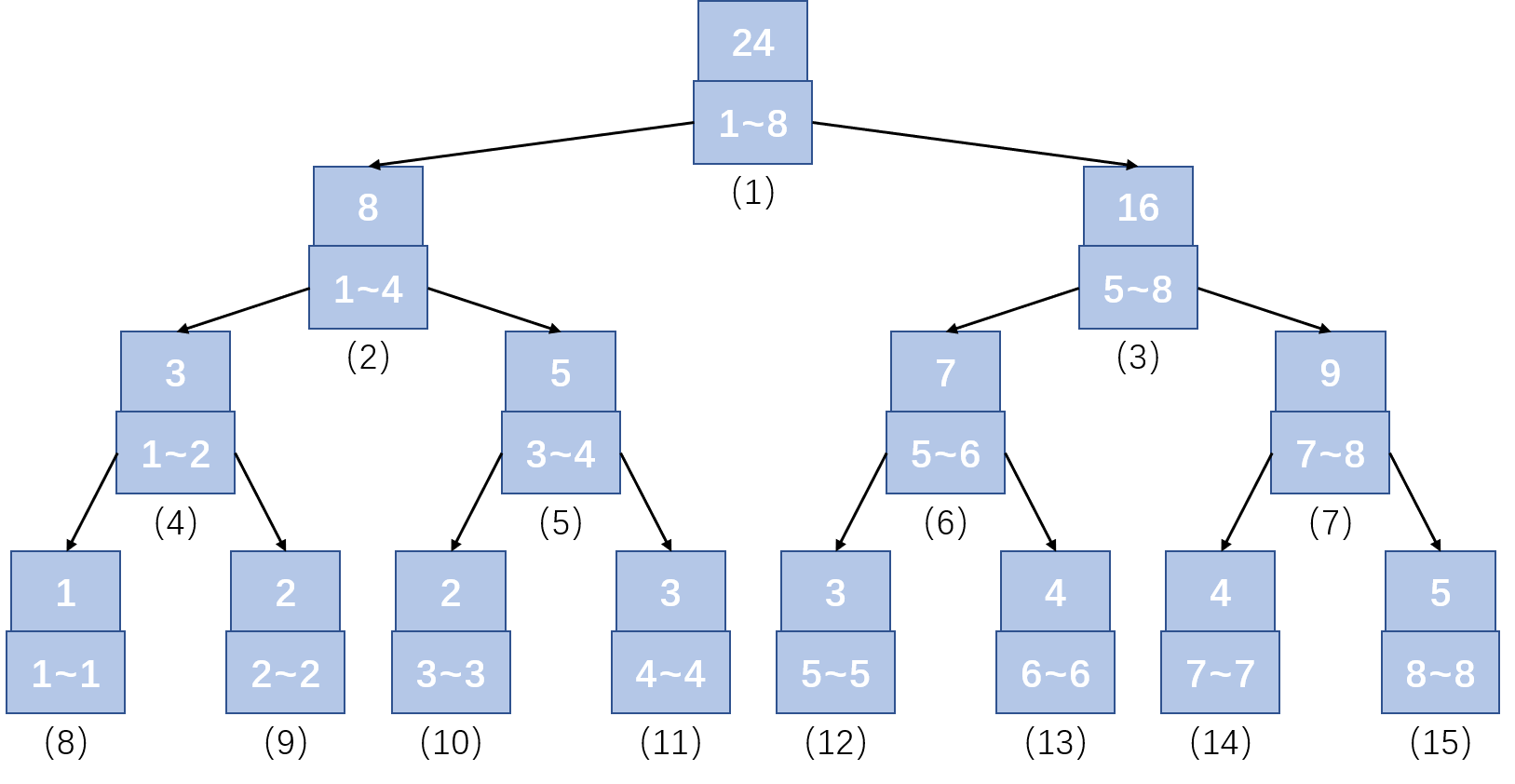
可以发现:一个节点的序号如果是k,那么左子节点的序号为2*k,右子节点的序号为2*k+1,由于这种对应关系,所以线段树在建树过程中不需要重新定义指针指向子节点。
父节点的区间为两个子节点的区间和:假设两个子节点存有初始序列l1~r1及l2~r2(r1<l2)的区间和,那么对应父节点存有l1~r2的区间和,叶子节点则只存有初始序列每一个点的值。
每一个节点都存有如图的四个变量,假设节点结构体名字叫tree,创建tree数组
1 struct p{ 2 int l;//区间左端点 3 int r;//区间右端点 4 int sum;//区间和 5 }tree[4*n];//4倍空间
ps:注意用结构体数组存节点信息时,如果初始序列区间长为n,那么结构体数组要开4*n的空间!
证明:
假设区间长为n,那么线段树最下面一次至多有n个节点,则这棵树有⌈log2n⌉+1层,由于 ⌈log2n⌉小于等于log2n+1。所以这棵树至多有log2n+2层,根据二叉树的节点个数与层数的关系可知,这棵树至多有2log2n+2=4*n个节点。
建树
线段树建树采用递归+回溯的方式,线段树第一个节点tree[1].sum存的是初始序列nu[1]到nu[n]的区间和。
对于任意一个节点,如果这个节点存的是初始序列nu[l]到nu[r]的区间和,那么左子节点存的是nu[l]到nu[(l+r)/2]的区间和,右子节点存的是nu[(l+r)/2+1]到nu[r]的区间和。
采用递归加回溯方法,从第一个节点tree[1]开始创建,每当我们创建一个节点时:
如果这个节点是叶子节点,由于叶子节点存的是初始序列的单点值,就只用直接对叶子节点的sum值输入值就行了,然后返回。
如果这个节点不是叶子节点,我们就创建这个节点的左子节点,然后创建这个节点的右子节点,创建完毕后会回到当前节点,然后将左子节点的sum值+右子节点的sum值赋给当前节点的sum值;
具体步骤如下:
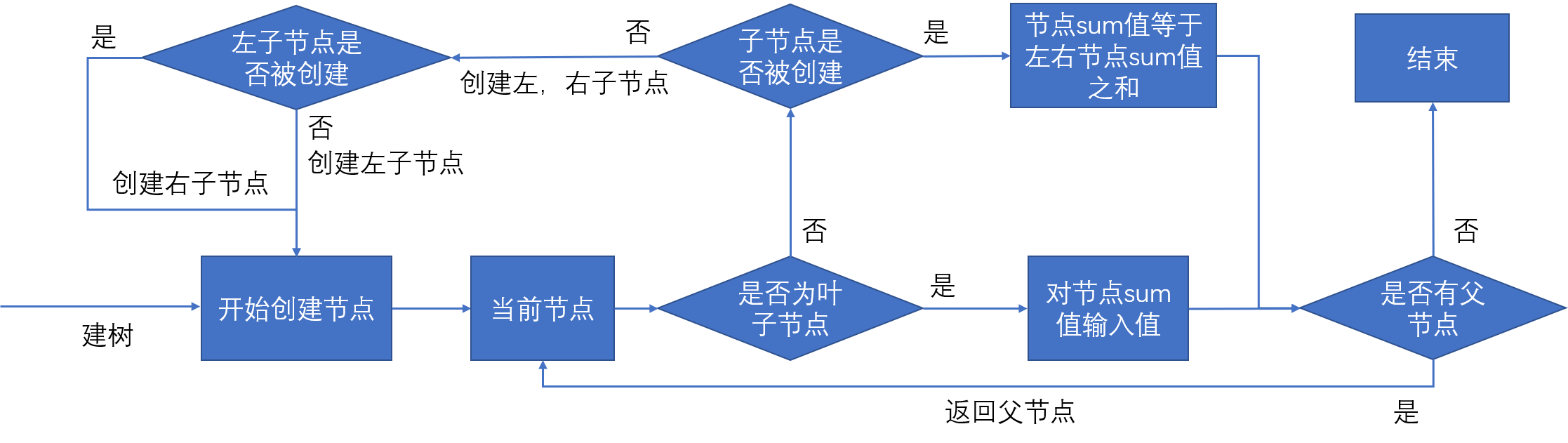
代码如下:
1 void build(int l,int r,int k){//l是区间左端点,r是区间右端点,k是节点序号 2 tree[k].l=l; 3 tree[k].r=r; 4 if(l==r){//表示是叶子节点 5 cin>>tree[k].sum; 6 return; 7 } 8 int pos=(l+r)/2; 9 build(l,pos,2*k);//创建左子节点 10 build(pos+1,r,2*k+1);//创建右子节点 11 //创建完毕 12 tree[k].sum=tree[2*k].sum+tree[2*k+1].sum; //当前节点所存的区间和等于左右子节点所存区间和 13 return; 14 }
单点查询
单点查询需要二分递归子节点,假如要查询nu[m]的值
每当我们递归到一个节点tree[x],先判断此节点是否为叶子节点:
如果是叶子节点,则说明此节点存的就是nu[m]的单点值,直接返回tree[m].sum的值;
如果不是叶子节点,则说明此节点存的是nu的区间值,区间左端为l,右端为r,判断m与(l+r)/2的关系:
如果m<=(l+r)/2,则说明nu[n]的值存到了左子节点中,递归左子节点;
如果m>(l+r)/2,则说明nu[n]的值存到了右子节点中,递归右子节点;
代码如下:
1 int ask(int x,int k){ 2 if(tree[k].l==tree[k].r) return tree[k].sum;//叶子节点直接返回值 3 if(tree[k].lazy) push(k); 4 int pos=(tree[k].l+tree[k].r)/2; 5 return (x<=pos)?ask(x,2*k):ask(x,2*k+1);//不是叶子节点返回二分递归后的值 6 }
单点修改
单点修改也是从tree[1]开始二分递归,假如我们想修改nu[m]的值(但其实我们仍然是对线段树的叶子节点进行修改,并没有修改初始序列)
每当我们递归到一个节点tree[x],先判断此节点是否为叶子节点:
如果是叶子节点,则说明此节点存的就是nu[m]的单点值,直接对tree[x].sum进行修改,然后返回;
如果不是叶子节点,则说明此节点存的是nu的区间值,区间左端为l,右端为r,判断m与(l+r)/2的关系:
如果m<=(l+r)/2,则说明nu[n]的值存到了左子节点中,递归左子节点;
如果m>(l+r)/2,则说明nu[n]的值存到了右子节点中,递归右子节点;
注意,在修改完毕回溯的时候,由于子节点的sum值以及被修改,故还要进行状态合并:
tree[k].sum=tree[2*k].sum+tree[2*k+1].sum;
代码如下:
1 void add(int x,int z,int k){ 2 if(tree[k].l==tree[k].r){//判断是否为叶子节点 3 // return (void)(tree[k].sum=z);//使用这个语句则进行单点赋值修改 4 return (void)(tree[k].sum+=z);//使用这个语句则进行单点加值修改 5 } 6 int pos=(tree[k].l+tree[k].r)/2; 7 if(x<=pos) add(x,z,2*k); 8 else add(x,z,2*k+1); 9 tree[k].sum=tree[2*k].sum+tree[2*k+1].sum;//不要忘记在回溯过程中要进行状态合并 10 return; 11 }
ps:注意,如果你想要单点赋值修改某个值,就用第一条语句;如果想要单点加值修改,就用第二条语句;二选一
区间查询
区间查询较单点查询有一点复杂,虽然也需要递归节点,但是节点所存的区间范围和需要查询的区间范围可能出现多种情况。
当我们从第一个节点开始递归,每次递归到一个节点可能会发生下列情况:
1.查找区间(l-r)包含节点区间(L-R)
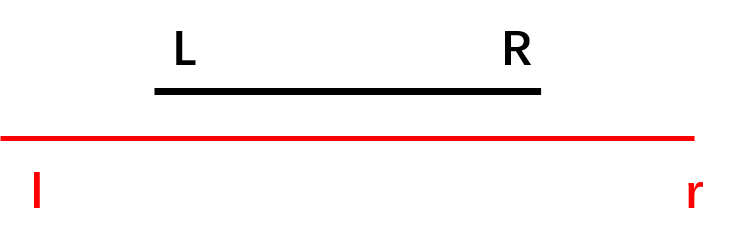
这种情况就说明节点所存的区间和属于我们需要查询的区间和之内,直接返回当前节点所存的区间和。
if(tree[k].l>=l && tree[k].r<=r) return tree[k].sum;
2.节点区间(L-R)与查找区间(l-r)有重叠部分
 或者
或者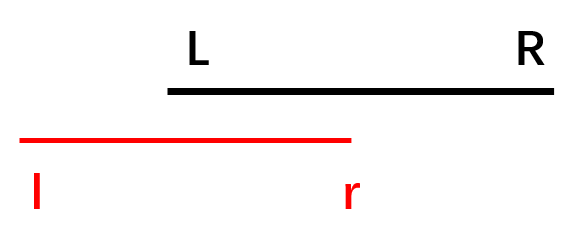
这种情况需要继续递归当前节点的左右节点:
如果l<=(L+R)/2,则需要递归查找左子节点,直到出现第一种情况;
如果r>(L+R)/2,则需要递归查找右子节点,直到出现第一种情况;
ps:以上两种情况(l<=(L+R)/2且r>(L+R)/2)如果都发生了,则左右子节点都要递归。
int pos=(tree[k].l+tree[k].r)/2; return (l<=pos?sum(l,r,2*k):0)+(r>pos?sum(l,r,2*k+1):0);//加号用来合并两种情况
代码如下:
1 int sum(int l,int r,int k){//l表示查询区间的左端点,r表示查找区间右端点,k表示当前递归的节点的序号 2 if(tree[k].l>=l && tree[k].r<=r) return tree[k].sum; 3 int pos=(tree[k].l+tree[k].r)/2; 4 return (l<=pos?sum(l,r,2*k):0)+(r>pos?sum(l,r,2*k+1):0); 5 }
3.节点区间(L-R)包含查找区间(l-r)

这种情况看似新奇,其实和第二种情况并没有多大区别,仍然和第二种情况一样对待。
只不过这恰好是第二种情况中l<=(L+R)/2且r>(L+R)/2同时发生的情况。
int pos=(tree[k].l+tree[k].r)/2; return (l<=pos?sum(l,r,2*k):0)+(r>pos?sum(l,r,2*k+1):0);//加号用来合并两种情况
区间修改
线段树的区间修改时线段树独有的核心重点。可能有人根据单点修改和区间查询,想出一种区间修改(加值修改)的方法:
从第一个节点往子节点递归,每当递归到一个节点,如果是叶子节点就修改值,然后返回;不是叶子节点就根据区间查询的情况进行递归子节点。
这的确是一种方法,但是这种方法不仅要修改区间内的所有叶子节点,还要修改叶子节点对应的所有父节点,复杂度大大的提高了。
如果修改全部的节点,复杂度当然高,如果我们只修改一部分具有代表性的节点,然后以这些代表性的节点来表示所有被应该修改的节点,这样复杂度就降低了。
于是,在区间修改中,引入了一个新的变量,叫做“延迟标记”,延迟标记是一个数,每个节点都有延迟标记,且初始化为0。
struct p{ int l;//区间左端点 int r;//区间右端点 int sum;//区间和 int lazy;//延迟标记 }tree[4*n];//4倍空间
如果某个节点的延迟标记为m,代表以此节点为根节点的树的所有叶子节点的值都要加上m,如下图所示(看不清楚可以点击放大看)

如图,圆形中的数就是延迟标记。总的来讲,如果一个节点tree[n]的延迟标记为m,不仅仅是以tree[n]为根节点的树的所有叶子节点要加上m,左右子数衍生出来的所有节点都要加上节点区间长度*m,即(r-l+1)*m。
当然,在递归节点过程中,如果要给一个节点被加上了延迟标记,就必须保证左右子树所存的区间都是包含于需要修改的区间中,即

其中需要修改的区间是(l-r),当前节点区间为(L-R),这种情况下就不用继续递归子节点,直接给当前节点加上延迟标记,因为你已经知道当前节点的所有子节点都要被修改,延迟标记的值是可以叠加的,毕竟延迟标记代表着左右子树节点都要加上一个某值,加法当然是可以叠加的。
if(tree[k].l>=l && tree[k].r<=r){ tree[k].sum+=(tree[k].r-tree[k].l+1)*x; tree[k].lazy+=x; return; }
但是你有没有想过,如果之前某次区间修改已经给一个节点加上了延迟标记,此后又一次区间修改刚好又递归到这个节点,且还需要继续递归这个节点的子节点,那该怎么办?
这时,就需要把延迟标记往下推,并只用更新左右子节点的值,然后把当前节点的标记清除,如下图所示(看不清楚可以点击放大看)
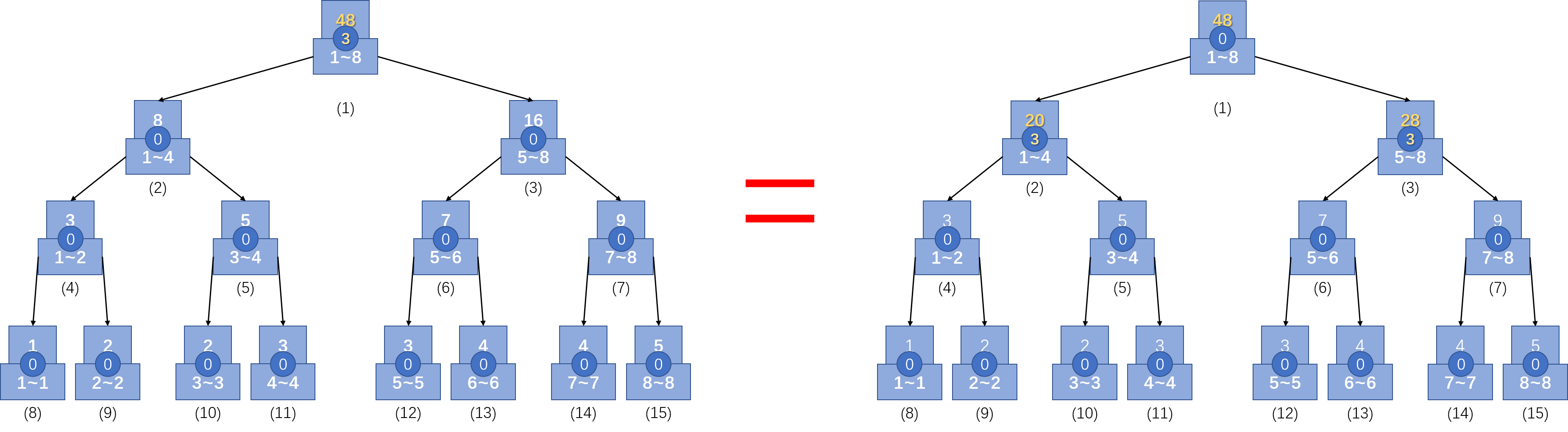
走一步,推一步,只更改了有用的节点的sum值。
1 void push(int k){ 2 tree[2*k].lazy+=tree[k].lazy; 3 tree[2*k+1].lazy=+tree[k].lazy; 4 tree[2*k].sum+=(tree[2*k].r-tree[2*k].l+1)*tree[k].lazy; 5 tree[2*k+1].sum+=(tree[2*k+1].r-tree[2*k+1].l+1)*tree[k].lazy; 6 tree[k].lazy=0; 7 return; 8 }
于是,整个区间修改的代码就完成了(说明一下,把标记往下推,指的是推向左右子节点)
1 void push(int k){ 2 tree[2*k].lazy+=tree[k].lazy; 3 tree[2*k+1].lazy+=tree[k].lazy; 4 tree[2*k].sum+=(tree[2*k].r-tree[2*k].l+1)*tree[k].lazy; 5 tree[2*k+1].sum+=(tree[2*k+1].r-tree[2*k+1].l+1)*tree[k].lazy; 6 tree[k].lazy=0; 7 return; 8 } 9 void change(int l,int r,int x,int k){ 10 if(tree[k].l>=l && tree[k].r<=r){//表示不用继续递归,可以合并延迟标记 11 tree[k].sum+=(tree[k].r-tree[k].l+1)*x; 12 tree[k].lazy+=x; 13 return; 14 } 15 //下面表示还需要递归,要把延迟标记往下推 16 if(tree[k].lazy) push(k);//如果当前节点没有延迟标记,就不用推了 17 int pos=(tree[k].r+tree[k].l)/2; 18 if(l<=pos) change(l,r,x,2*k); 19 if(r>pos) change(l,r,x,2*k+1); 20 return; 21 }
更多类型延迟标记
关于区间修改这一部分,应该对延迟标记有一些了解,但是之前区间修改中的延迟标记,只是代表着左右子树的叶子节点要加上某一个值,这就属于一种加值标记。
除了加值标记以外,还有一种标记叫做赋值标记。顾名思义,如果一个节点具有一个非零的赋值标记,则代表着左右子树的叶子节点要被赋上一个值。
可以看出,赋值标记的优先度比加值标记要高,即一个节点的加值标记不管为多少,如果再给这个节点加上一个赋值标记,那这个节点的加值标记就需要被清零。赋值标记是不能叠加的。
这是将赋值标记往下推的代码,与加值标记下推代码不同的是,赋值标记中的符号发生了改变(可以对比看看)。
1 void push(int k){ 2 tree[2*k].lazy=tree[k].lazy; 3 tree[2*k+1].lazy=tree[k].lazy; 4 tree[2*k].sum=(tree[2*k].r-tree[2*k].l+1)*tree[k].lazy; 5 tree[2*k+1].sum=(tree[2*k+1].r-tree[2*k+1].l+1)*tree[k].lazy; 6 tree[k].lazy=0; 7 return; 8 }
这是区间赋值修改的代码,与区间加值修改代码的不同的地方已经高亮显示。
1 void push(int k){ 2 tree[2*k].lazy=tree[k].lazy; 3 tree[2*k+1].lazy=tree[k].lazy; 4 tree[2*k].sum=(tree[2*k].r-tree[2*k].l+1)*tree[k].lazy; 5 tree[2*k+1].sum=(tree[2*k+1].r-tree[2*k+1].l+1)*tree[k].lazy; 6 tree[k].lazy=0; 7 return; 8 } 9 void change(int l,int r,int x,int k){ 10 if(tree[k].l>=l && tree[k].r<=r){ 11 tree[k].sum=(tree[k].r-tree[k].l+1)*x; 12 tree[k].lazy=x; 13 return; 14 } 15 if(tree[k].lazy) push(k); 16 int pos=(tree[k].r+tree[k].l)/2; 17 if(l<=pos) change(l,r,x,2*k); 18 if(r>pos) change(l,r,x,2*k+1); 19 return; 20 }
除此之外,赋值标记和加值标记是不能共存的,它们具有以下关系:
如果一个节点原本就有赋值标记:
此时如果加上一个加值标记,那么就将赋值标记推向子节点,然后更新当前节点的加值标记;
此时如果加上一个赋值标记,那么将新的赋值标记覆盖原本的赋值标记。
如果一个节点原本就有加值标记:
此时如果加上一个加值标记,那么将新的加值标记叠加到原本的加值标记。
此时如果加上一个赋值标记,那么清除当前节点的加值标记,直接更新当前节点的赋值标记。
当然,标记的种类多种多样,只要给标记一个不同定义,它就能对区间修改产生不一样的效果。
延迟标记对其他操作的影响
首先强调一点,我们讨论的延迟标记仍然是加值延迟标记,其他操作指线段树除区间修改之外的操作,单点修改和区间修改默认为加值修改。
延迟标记对单点查询的影响
由于单点查询是递归到特定的叶子节点上,所以在递归的过程中,还要一起把节点的延迟标记往下推(更新子节点sum值)
所以加入延迟标记后的代码
1 int ask(int x,int k){ 2 if(tree[k].l==tree[k].r) return tree[k].sum; 3 if(tree[k].lazy) push(k); 4 int pos=(tree[k].l+tree[k].r)/2; 5 return (x<=pos)?ask(x,2*k):ask(x,2*k+1); 6 }
延迟标记对单点修改的影响
对某一点的修改只针对某一个点来说,由于加值是可以叠加的,所以延迟标记对单点修改时没有影响的。
代码仍然为
1 void add(int x,int z,int k){ 2 if(tree[k].l==tree[k].r){ 3 // return (void)(tree[k].sum=z); 4 return (void)(tree[k].sum+=z); 5 } 6 int pos=(tree[k].l+tree[k].r)/2; 7 if(x<=pos) add(x,z,2*k); 8 else add(x,z,2*k+1); 9 tree[k].sum=tree[2*k].sum+tree[2*k+1].sum; 10 return;
延迟标记对区间查询的影响
区间查询和单点修改一样,需要把延迟标记往下推,才能得到真正被修改后的值(不断的更新节点sum值)
代码如下
1 void change(int l,int r,int x,int k){ 2 if(tree[k].l>=l && tree[k].r<=r){ 3 tree[k].sum+=(tree[k].r-tree[k].l+1)*x; 4 tree[k].lazy+=x; 5 return; 6 } 7 if(tree[k].lazy) push(k); 8 int pos=(tree[k].r+tree[k].l)/2; 9 if(l<=pos) change(l,r,x,2*k); 10 if(r>pos) change(l,r,x,2*k+1); 11 return; 12 }
总结代码
建树,单点修改,单点查询,区间修改,区间查询
#include <iostream> using namespace std; const int n=5;//初始序列长度 struct p{ int l;//区间左端点 int r;//区间右端点 int sum;//区间和 int lazy;//标记 }tree[4*n];//4倍空间 void push(int k){ //向下推加值标记 tree[2*k].lazy+=tree[k].lazy; tree[2*k+1].lazy+=tree[k].lazy; tree[2*k].sum+=(tree[2*k].r-tree[2*k].l+1)*tree[k].lazy; tree[2*k+1].sum+=(tree[2*k+1].r-tree[2*k+1].l+1)*tree[k].lazy; tree[k].lazy=0; //向下推赋值标记 // tree[2*k].lazy=tree[k].lazy; // tree[2*k+1].lazy=tree[k].lazy; // tree[2*k].sum=(tree[2*k].r-tree[2*k].l+1)*tree[k].lazy; // tree[2*k+1].sum=(tree[2*k+1].r-tree[2*k+1].l+1)*tree[k].lazy; // tree[k].lazy=0; return; } int sum(int l,int r,int k){//区间查询 if(tree[k].l>=l && tree[k].r<=r) return tree[k].sum; int pos=(tree[k].l+tree[k].r)/2; return (l<=pos?sum(l,r,2*k):0)+(r>pos?sum(l,r,2*k+1):0); } void build(int l,int r,int k){//建树 tree[k].l=l; tree[k].r=r; if(l==r){//表示是叶子节点 cin>>tree[k].sum; return; } int pos=(l+r)/2; build(l,pos,2*k);//创建左子节点 build(pos+1,r,2*k+1);//创建右子节点 //创建完毕 tree[k].sum=tree[2*k].sum+tree[2*k+1].sum; //当前节点所存的区间和等于左右子节点所存区间和 return; } int ask(int x,int k){//单点查询 if(tree[k].l==tree[k].r) return tree[k].sum; if(tree[k].lazy) push(k); int pos=(tree[k].l+tree[k].r)/2; return (x<=pos)?ask(x,2*k):ask(x,2*k+1); } void add(int x,int z,int k){//单点修改 if(tree[k].l==tree[k].r){ // return (void)(tree[k].sum=z);//单点赋值修改 return (void)(tree[k].sum+=z);//单点加值修改 } int pos=(tree[k].l+tree[k].r)/2; if(x<=pos) add(x,z,2*k); else add(x,z,2*k+1); tree[k].sum=tree[2*k].sum+tree[2*k+1].sum; return; } void change(int l,int r,int x,int k){//区间修改 if(tree[k].l>=l && tree[k].r<=r){ // 区间加值修改 tree[k].sum+=(tree[k].r-tree[k].l+1)*x; tree[k].lazy+=x; // 区间赋值修改 // tree[k].sum=(tree[k].r-tree[k].l+1)*x; // tree[k].lazy=x; return; } if(tree[k].lazy) push(k); int pos=(tree[k].r+tree[k].l)/2; if(l<=pos) change(l,r,x,2*k); if(r>pos) change(l,r,x,2*k+1); tree[k].sum=tree[2*k].sum+tree[2*k+1].sum; return; }
说明:在build函数中,l指区间左端点(一般为1),r指区间右端点(一般为n),k为开始节点序号(为1);
在ask函数中,x表示查询初始序列nu[x]的值,k为开始节点序号(为1);
在add函数中,x表示修改初始序列nu[x]的值,z表示需要加上的值,k为开始节点序号(为1);
在sum函数中,l表示查询区间左端点,r表示查询区间右端点,k为开始节点序号(为1);
在change函数中,l表示修改区间左端点,r表示修改区间右端点,x表示需要加上的值,k为开始节点序号(为1);
其中:节点数组为tree[],n表示初始序列长度
main函数测试:

int main(){ build(1,n,1);//1,2,3,4,5 cout<<sum(1,n,1)<<endl;//15 add(1,2,1);//3,2,3,4,5 cout<<ask(1,1)<<endl;//3 change(1,n,1,1);//4,3,4,5,6 cout<<sum(1,n,1)<<endl;//22 return 0; }
