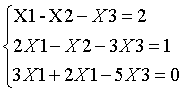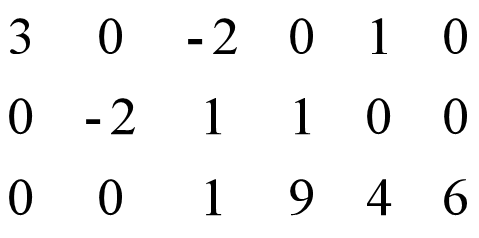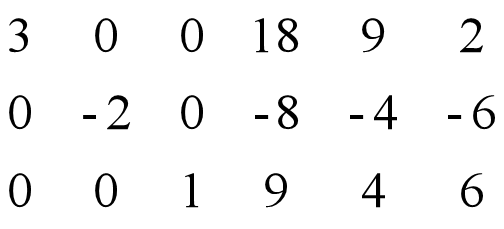一般的高斯消元需要回代,所以就显得比较赘余,一般选用高斯-约旦消元法
关于高斯消元你就可以简单理解为加减消元得到一个上三角矩阵
而高斯约旦消元就是转化为对角矩阵
首先给定一个多元一次方程组
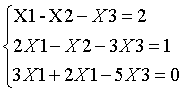
我们可以直接写A出它的增广矩阵直接求出他的解
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define re register
const int maxn=300;
int n;
double a[maxn][maxn];
bool f()
{
for(re int i=1,t;i<=n;++i)
{
t=i;
for(re int j=i+1;j<=n;++j)///找出每一列的最大主元
{
if(fabs(a[j][i])>fabs(a[t][i]))///找寻最大主元
{
t=j;
}
}
if(i^t)///相当于i!=t,保证不在当前行
{
swap(a[i],a[t]);///交换行
}
if (a[i][i]==0)///主元为0,直接无解
{
printf("No Solution
");
return false;
}
for(re int j=1;j<=n;++j)
{
if(j!=i)///对角主元不变化
{
double tmp=a[j][i]/a[i][i];
for(int k=i;k<=n+1;++k)
{
a[j][k]=(a[j][k]-a[i][k]*tmp);
}
}
}
//for(re int j=1;j<=n+1;++j)a[i][j]=(a[i][j]/a[i][i]);///注释是为了比较下面的求逆矩阵
}
return true;
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;++i)
{
for (int j=1;j<=n+1;++j)
{
scanf("%lf",&a[i][j]);
}
}
if (f())
for (int i=1;i<=n;++i)
printf("%.2f
",a[i][n+1]/a[i][i]);///此时直接就是对角矩阵直接除以对角的主元
return 0;
}
同理对于方矩阵A
我们可以利用初等变化求出它的逆矩阵
证明如下:
对于矩阵(A,B)进行初等变化变为(E,P)易知p就是A的逆矩阵
关于高斯-约旦消元法就是利用此种方法求解

接下来进行初等变化
分为步
1.找出第I列的主元(元素值最大的那个)然后交换到第I行(已经交换到前面的就无需考虑)
2.求出对角线也就是第(i,i)个元素的逆元(由于需要mod,所以该逆元可以理解为他的倒数
3.直接更改当前行乘以逆元,你会发现第(i,i)个元素直接就是1
4.所以随后只要减去1*该列除了主元以外其他元素的值,依次消元
如下图所示1.
2. 
3. 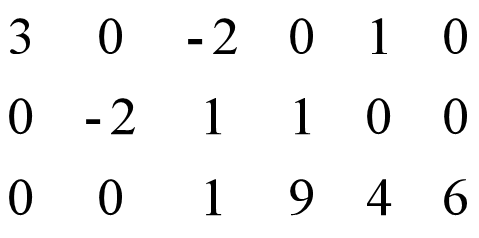
4. 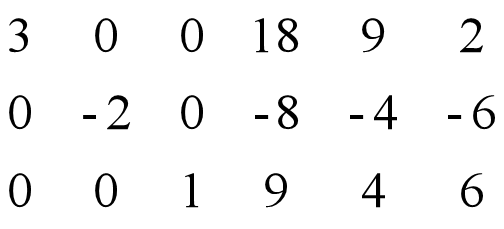

由于此处需要%,所以除法取模一般采用逆元
代码如下
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define re register
const int maxn=300;
const int mod=998244353;
ll a[maxn][maxn<<1];
ll quickpow(ll a,ll b,ll p)
{
ll ans=1;
while (b)
{
if (b&1)///b为奇数
ans=(ans*a)%p;
a=(a*a)%p;///b为偶数
b>>=1;
}
return ans;
}
for(re int i=1,t;i<=n;++i)
{
t=i;
for(re int j=i+1;j<=n;++j)///找出每一列的最大主元
{
if(abs(a[j][i])>abs(a[t][i]))///找寻最大主元
{
t=j;
}
}
if(i^t)///相当于i!=t,保证不在当前行
{
swap(a[i],a[t]);///交换行
}
ll w=quickpow(a[i][i],mod-2,mod);///直接求出对角元素值,方便消元
for(re int j=1;j<=n;++j)
{
if(j!=i)///当前行直接乘以逆元即可,无需进行消元
{
ll tmp=a[j][i]*w%mod;///主元乘以逆元
for(int k=i;k<=(n<<1);++k)
{
a[j][k]=((a[j][k]-a[i][k]*tmp)%mod+mod)%mod;///该点元素直接减去i行元素乘以对称点(i i)的逆元
}
}
}
for(re int j=1;j<=(n<<1);++j)a[i][j]=(w*a[i][j])%mod;///最后当前行直接乘以逆元保证主元为1,更新当前行,保证最后能得到单位矩阵
///对比上面的求解线性方程,此处是为了更新增广矩阵
}