容斥原理（三元容斥，四元容斥）

题意：　　　　已知集合A，B，C，输出三集合的并集。

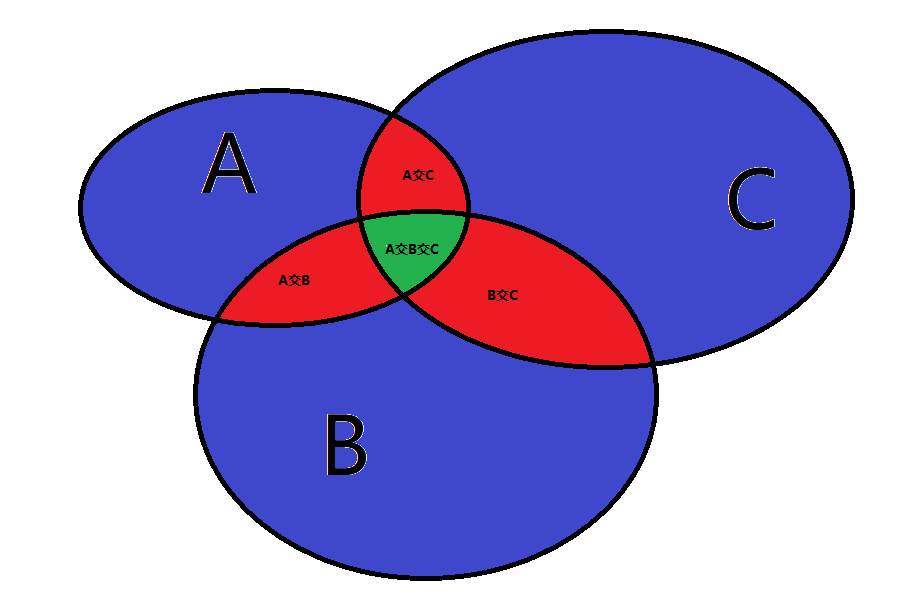
容斥原理（用图解释）

∩

∪

对于求三集合并集的公式：

　　A∪B∪C=A+B+C - A∩B - A∩C - B∩C + A∩B∩C

　　对于证明，我就简单的叙述一下。

　　　　因为求并集不能将两集合的重复元素进行相加。而 A+B+C 没有考虑重复元素，直接相加，显然这是元素多加的情况，那要还原必须要减去多加的部分，对于上图蓝色部分只加了一次，红色部分加了两次，绿色的部分加了三次，那么我们只需要使他们全部只加一次就能得到正确答案。

所以我们要执行下操作 A+B+C -（A∩B + A∩C + B∩C），但还不算完美，因为在这里绿色部分被减了三次，要使把绿色部分只减一次，那么要再加上一个绿色部分即可。

对于求四集合并集的公式：

A∪B∪C∪D=A+B+C+D - A∩B - B∩C - C∩A - A∩D - B∩D - C∩D + A∩B∩C + A∩B∩D + A∩C∩D + B∩C∩D - A∩B∩C∩D （ 规律集合数奇加偶减）

对于证明类似于上列三元并集证明。

贴一题目（四元）：

给出一个数N，求1至N中，有多少个数不是2 3 5 7的倍数。 例如N = 10，只有1不是2 3 5 7的倍数。
 
输入
输入1个数N(1 <= N <= 10^18)。
输出
输出不是2 3 5 7的倍数的数共有多少。
输入样例
10
输出样例
1

AC代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<stack>
#include<algorithm>
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define Mem0(x) memset(x,0,sizeof(x))
#define Mem1(x) memset(x,-1,sizeof(x))
#define MemX(x) memset(x,0x3f,sizeof(x))
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f;
const double pi=acos(-1.0);

ll n;
int main()
{
    ll ans=0;
    cin>>n;
    ans=n/2+n/3+n/5+n/7;
    ans=ans-n/6-n/10-n/14-n/15-n/21-n/35+n/30+n/42+n/105+n/70-n/210;
    cout<<n-ans<<endl;
    return 0;
}

再贴一题：（提供链接，就不贴题目了）

https://ac.nowcoder.com/acm/contest/634/C

解题：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<stack>
#include<algorithm>
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
#define Mem0(x) memset(x,0,sizeof(x))
#define Mem1(x) memset(x,-1,sizeof(x))
#define MemX(x) memset(x,0x3f,sizeof(x))
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f;
const double pi=acos(-1.0);


ll l,r,k;
ll prime[500050];
bool check[1000010];
int cnt;
void prim()
{
    memset(check,false,sizeof(check));
    check[0]=check[1]=true;
    cnt=0;
    for (int i=2;i<500000;i++){
        if (!check[i])
            prime[cnt++]=i;
        for (int j=0;j<cnt&&i*prime[j]<1000000;j++){
            check[i*prime[j]]=true;
            if (i%prime[j]==0)
                break;
        }
    }
}
ll a[1000010];
int main()
{
    prim();
    cin>>l>>r>>k;
    ll p=0;//质因数的个数 
    ll tmp=k<<1;
/*    for (int i=0;;i++){
        if (tmp%prime[i]==0){
            a[p++]=prime[i];
            while (tmp%prime[i]==0){
                tmp/=prime[i];
            }
        }
        if (tmp<=1)
            break;
    }*/
    for(int i=2;i*i<=tmp;i++){
        if(!(tmp%i)){
            a[p++]=i;
            while(!(tmp%i))
                tmp/=i;
        }
    }
    if(tmp>1)
        a[p++]=tmp;
    
    ll sum=0;
    tmp=1<<p;//  存在p个质数，则有pow（2，p）种的组合数,
    for (int i=0;i<tmp;i++){
        ll t=1,s=0;   //t是质因数的公倍数，s则为选举的质因数的个数 
        for (int j=0;j<p;j++){
            if (i&(1<<j)){
                s++;
                t*=a[j];
            }
        }
         if(r/t>(l+2*k-1)/t){  //容斥  奇加偶减 
            if(s%2)sum-=r/t-(l+2*k-1)/t;
            else sum+=r/t-(l+2*k-1)/t;
        }        
    }
    cout<<sum<<endl; 
    return 0;
}