任务安排1
初步思考可以得出一个(O(n^3))的dp做法
f[i][j]表示前i个任务,分成j段的最小费用
求出t和c的前缀和sumt[i]和sumc[i]
(f[i][j]=min{f[k][j-1]+(s*j+sumt[i])*(sumc[i]-sumc[k])})
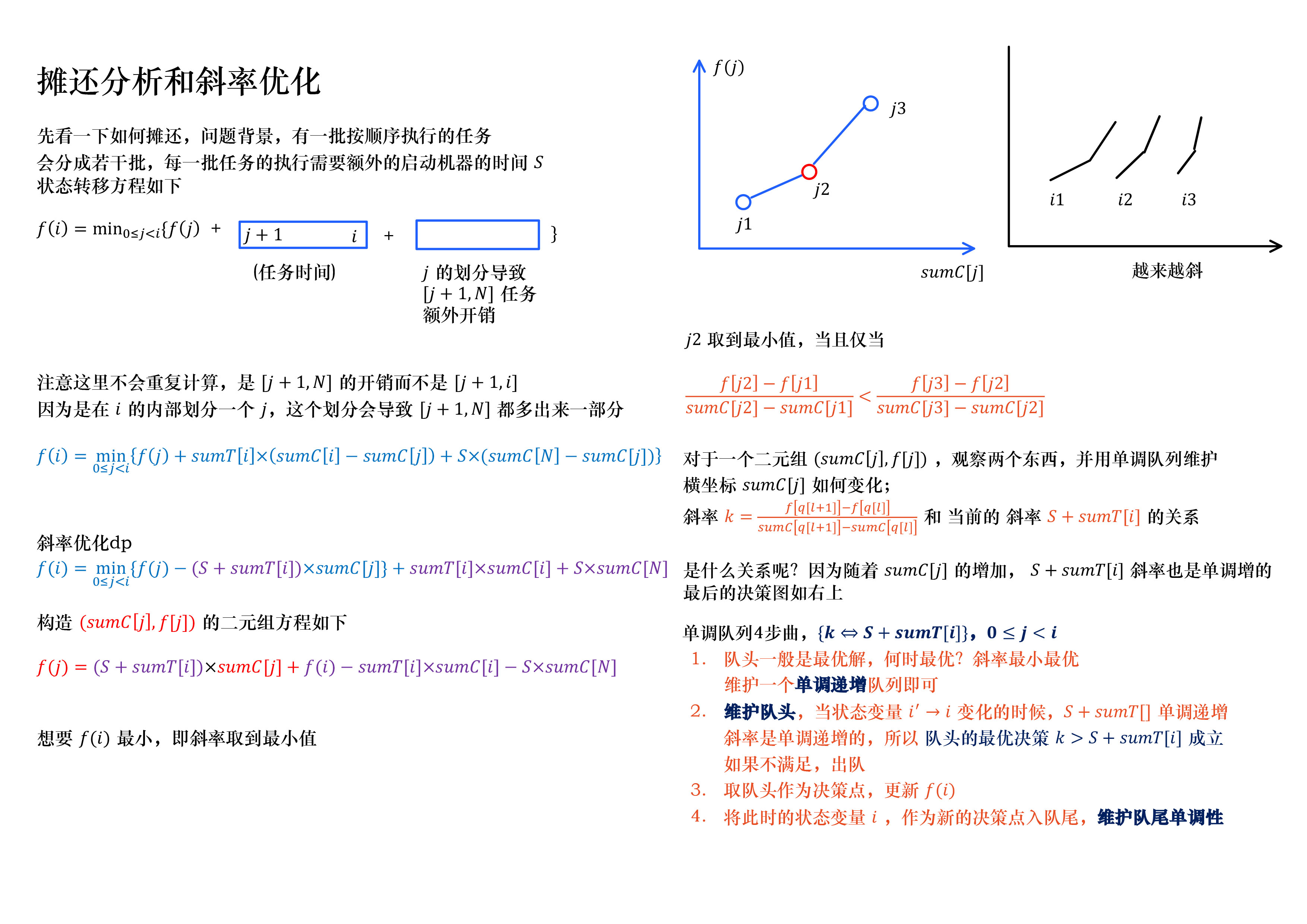
我们可以考虑把启动时间累加到后面所有任务的总时间上去
设f[i]表示前i个任务分成若干批执行的最小费用
(f[i]=min{f[j]+sumt[i]*(sumc[i]-sumc[j])+s*(sumc[n]-sumc[j])}(0<=j<i))
复杂度(O(n^2))
这是一种费用提前计算的经典思想
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
char c = getchar();
int x = 0, f = 1;
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}
const int N=5020;
int n,s,f[N],sumc[N],sumt[N];
signed main()
{
n=read(),s=read();
for(int i=1;i<=n;++i)
{
int t=read(),c=read();
sumt[i]=sumt[i-1]+t;
sumc[i]=sumc[i-1]+c;
}
memset(f,0x3f3f3f,sizeof(f));
f[0]=0;
for(int i=1;i<=n;++i)
for(int j=0;j<i;++j)
f[i]=min(f[j]+sumt[i]*(sumc[i]-sumc[j])+s*(sumc[n]-sumc[j]),f[i]);
cout<<f[n];
return 0;
}
任务安排2
上图来自心里没有一点AC数
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
char c = getchar();
int x = 0, f = 1;
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}
const int N=3e5+2020;
int n,s;
int sumc[N],sumt[N];//前缀和数组
int f[N];//dp数组
int q[N];//维护下凸壳的队列
signed main()
{
n=read(),s=read();
for(int i=1;i<=n;++i)
{
int t=read(),c=read();
sumc[i]=sumc[i-1]+c;
sumt[i]=sumt[i-1]+t;
}
memset(f,0x3f,sizeof(f));
f[0]=0;int l=1,r=1;
q[1]=0;
for(int i=1;i<=n;++i)
{
while(l<r&&(f[q[l+1]]-f[q[l]])<=(s+sumt[i])*(sumc[q[l+1]]-sumc[q[l]])) l++;
f[i]=f[q[l]]-(s+sumt[i])*sumc[q[l]]+sumt[i]*sumc[i]+s*sumc[n];
while(l<r&&(f[q[r]]-f[q[r-1]])*(sumc[i]-sumc[q[r]])>=(f[i]-f[q[r]])*(sumc[q[r]]-sumc[q[r-1]])) r--;
q[++r]=i;
}
cout<<f[n];
return 0;
}
任务安排3
acwing是本题数据会溢出long long ,建议去loj
和上一道题不同的是t可能是负数,所以横坐标sumt不在具有单调性,导致需要最小化截距的直线的斜率
(s+sumt[i])不在具有单调性,所以不能只保留凸壳上大于(s+sumt[i])的部分了。而是需要维护整个凸壳
可以在单调队列里二分查找一个位置p,让左侧线段斜率比(s+sumt[i])大,右边比(s+sumt[i])小
(p)即为最优决策,然后更新(f[i])即可
Loj可过
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
char c = getchar();
int x = 0, f = 1;
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}
const int N=5e5+2021;
int n,s;
int l,r;
int sumt[N],sumc[N],f[N],q[N];
int search(int i,int k)
{
if(l==r) return q[l];
int L=l,R=r;
while(L<R)
{
int mid=(L+R)>>1;
if(f[q[mid+1]]-f[q[mid]]<=k*(sumc[q[mid+1]]-sumc[q[mid]])) L=mid+1;
else R=mid;
}
return q[L];
}
signed main()
{
n=read(),s=read();
for(int i=1;i<=n;++i)
{
int t=read(),c=read();
sumt[i]=sumt[i-1]+t;
sumc[i]=sumc[i-1]+c;
}
l=1,r=1;q[1]=0;
for(int i=1;i<=n;++i)
{
int p=search(i,s+sumt[i]);
f[i]=f[p]-(s+sumt[i])*sumc[p]+sumt[i]*sumc[i]+s*sumc[n];
while(l<r&&(f[q[r]]-f[q[r-1]])*(sumc[i]-sumc[q[r]])>=(f[i]-f[q[r]])*(sumc[q[r]]-sumc[q[r-1]])) r--;
q[++r]=i;
}
cout<<f[n];
return 0;
}