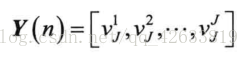BP神经网络是包含多个隐含层的网络,具备处理线性不可分问题的能力。以往主要是没有适合多层神经网络的学习算法,,所以神经网络的研究一直处于低迷期。
20世纪80年代中期,Rumelhart,McClelland等成立了Parallel Distributed Procession(PDP)小组,提出了著名的误差反向传播算法(Error Back Propagtion,BP)。
BP和径向基网络属于多层前向神经网络。广泛应用于分类识别、逼近、回归、压缩等领域。
BP神经网络(强调是用BP算法)一般是多层的,其概念和多层感知器(强调多层)差不多是等价的,隐层可以是一层或多层。BP神经网络具有如下特点:
(1)网络由多层构成,层与层之间全连接,同一层之间的神经元无连接。
(2)BP网络的传递函数必须可微。所以感知器的二值函数不能用,一般采用Sigmoid函数,可分为Log-Sigmoid和Tan-Sigmoid函数。
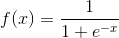
其中x的范围包含整个实数域,函数值再0~1之间。具体应用时可以增加参数,以控制曲线的位置和形状。
sigmoid函数可以将输入从负无穷到正无穷的范围映射到(-1,1)和(0,1)之间,在原点处具有非线性放大功能。BP的典型设计是隐含层采用Sigmoid函数作为传递函数,输出层采用线性函数作为传递函数。(一定不能全部层都采用线性的,否则就会和线性神经网络一样了)
(3)采用误差反向传播算法(Back-Propagation)进行学习。再BP网络中,数据从输入层经隐含层逐层向后传播,训练网络权值时,则沿着减少误差的方向,从输出层经过中间各层逐层向前修正网络连接权值。
(与反馈神经网络不同,BP是误差信号反向传播,网络根据误差从后向前逐层进行修正)
(1)网络由多层构成,层与层之间全连接,同一层之间的神经元无连接。
(2)BP网络的传递函数必须可微。所以感知器的二值函数不能用,一般采用Sigmoid函数,可分为Log-Sigmoid和Tan-Sigmoid函数。
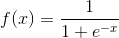
其中x的范围包含整个实数域,函数值再0~1之间。具体应用时可以增加参数,以控制曲线的位置和形状。
sigmoid函数可以将输入从负无穷到正无穷的范围映射到(-1,1)和(0,1)之间,具有非线性放大功能。
(3)采用误差反向传播算法(Back-Propagation)进行学习。再BP网络中,数据从输入层经隐含层逐层向后传播,训练网络权值时,则沿着减少误差的方向,从输出层经过中间各层逐层向前修正网络连接权值。
(与反馈神经网络不同,BP是误差信号反向传播,网络根据误差从后向前逐层进行修正)
(1)网络由多层构成,层与层之间全连接,同一层之间的神经元无连接。
(2)BP网络的传递函数必须可微。所以感知器的二值函数不能用,一般采用Sigmoid函数,可分为Log-Sigmoid和Tan-Sigmoid函数。
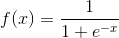
其中x的范围包含整个实数域,函数值再0~1之间。具体应用时可以增加参数,以控制曲线的位置和形状。
sigmoid函数可以将输入从负无穷到正无穷的范围映射到(-1,1)和(0,1)之间,具有非线性放大功能。
(3)采用误差反向传播算法(Back-Propagation)进行学习。再BP网络中,数据从输入层经隐含层逐层向后传播,训练网络权值时,则沿着减少误差的方向,从输出层经过中间各层逐层向前修正网络连接权值。
(与反馈神经网络不同,BP是误差信号反向传播,网络根据误差从后向前逐层进行修正)
BP算法的基本思想是,学习过程由信号的正向传播和误差的反向传播俩个过程组成,输入从输入层输入,经隐层处理以后,传向输出层。如果输出层的实际输出和期望输出不符合,就进入误差的反向传播阶段。误差反向传播是将输出误差以某种形式通过隐层向输入层反向传播,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,这个误差信号就作为修正个单元权值的依据。直到输出的误差满足一定条件或者迭代次数达到一定次数。
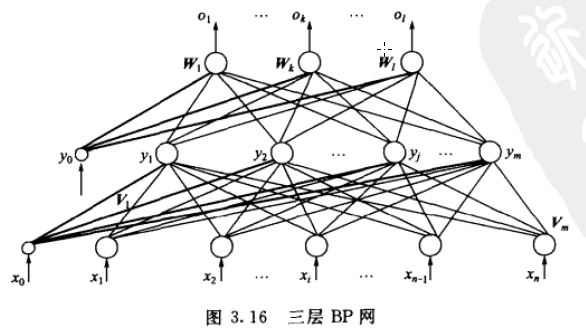
使用的传递函数sigmoid可微的特性使他可以使用梯度下降法。所以,在隐层函数中使用sigmoid函数作为传递函数,在输出层采用线性函数作为传递函数。
输入向量、隐层输出向量、最终输出向量、期望输出向量:
X=(x0,x1,x2,x3……xn),其中图中x0是为隐层神经元引入阈值设置的;x0=1
Y=(y0,y1,y2,y3……ym),其中图中y0是为输出神经元引入阈值设置的;y0=1
O=(o1,o2,o3……ol)
D=(d1,d2,d3……dl)
输出层的输入是隐层的输出,隐层的输入是输入层的输出,计算方法和单层感知器的计算方法一样。
BP网络的学习算法
确定层数和每层的神经元个数后,还需直到权值系数才能由输入给出正确的输出。
BP网络的学习属于有监督学习,需要一组已知目标输出的学习样本集。
先使用随机值作为权值,得到网络输出之后与期望输出作对比,然后根据输出值与期望值的计算误差,再由误差根据某种准则逐层修改权值,使得误差减小。
标准BP神经网络沿着误差性能函数梯度的反方向修改权值,原理与LMS算法比较类似,属于最速下降法。此外还有以下改进算法,如动量最速下降法,拟牛顿法等。
最速下降法又称为梯度下降法。LMS算法就是最小均方误差算法。LMS算法体现了纠错原则,与梯度下降法本质上没有区别,梯度下降法可以求目标函数的极小值,如果将目标函数取为均方误差,就得到了LMS算法。
梯度下降法原理:对于实值函数F(x),如果函数在某点x0处有定义且可微,则函数在该点处沿着梯度相反的方向下降最快,因此,使用梯度下降法时,应首先计算函数在某点处的梯度,再沿着梯度的反方向以一定的步长调整自变量的值。其中实值函数指的是传递函数,自变量x指的是上一层权值和输入值的点积作为的输出值。
网络误差定义:





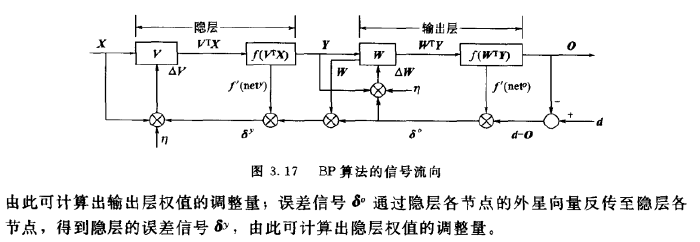
注意:
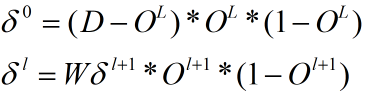
其中D表示输入数据的正确输出列向量,O表示网络对应层的输出列向量,W表示Wij的转秩矩阵,这就是每层反向传播的误差信号的矩阵计算式。
每一个权值参数的调整原则都是通过求其关于输出误差的导数。然后进行权值的调整。
以上摘选自韩力群《人工神经网络理论,设计及应用》,写的是很详细了
BP神经网络反向传播推导
1.变量定义
在三层神经网络中,假设输入神经元个数为M,隐含神经元个数为I,输出神经元个数为J。
输入层第m个神经元为Xm,隐藏层第i个神经元为Ki,输出层第j个神经元为Yj,从Xm到Ki的链接权值为Wmi,从Ki到Yj的链接权值为Wij,隐藏层使用Sigmoid函数,输出层使用功能线性函数。
U,V表示每层的输入与输出,UI表示输入层的输入,UM表示隐藏层的输入,UJ表示输出层的输入。VI,VM,VJ也与此一一对应。
注意,除了输出层,每一层还应该添加一个单元
网络的实际输出:
- 信号正向传播
- 误差信号反向传播
首先误差反向传播首先经过输出层,所以首先调整隐含层和输出层之间的权值。
然后对输入神经元和隐层神经元的误差进行调整。
权值矩阵的调整可以总结为:
权值调整量det(w)=学习率*局部梯度*上一层输出信号。
BP神经网络的复杂之处在于隐层输入层、隐层和隐层之间的权值调整时,局部梯度的计算需要用到上一步计算的结果,前一层的局部梯度是后一层局部梯度的加权和。
训练方式:
-
串行方式:网络每获得一个新样本,就计算一次误差并更新权值,直到样本输入完毕。
-
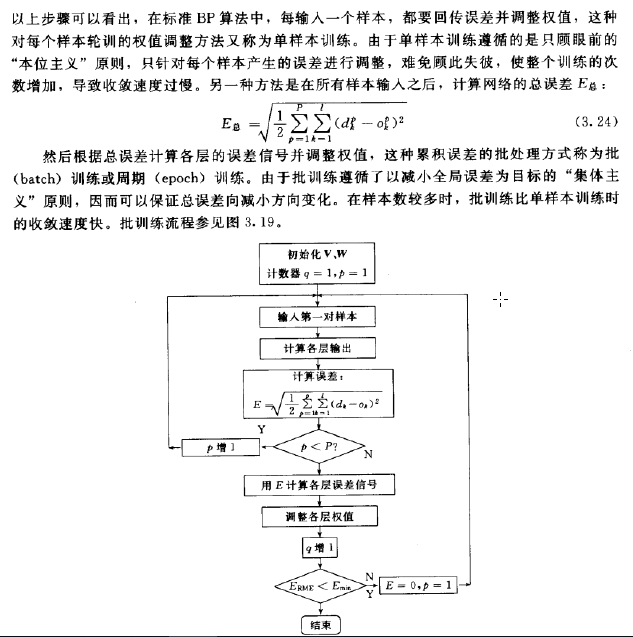
批量方式:网络获得所有的训练样本,计算所有样本均方误差的和作为总误差;
在串行运行方式中,每个样本依次输入,需要的存储空间更少,训练样本的选择是随机的,可以降低网络陷入局部最优的可能性。
批量学习方式比串行方式更容易实现并行化。由于所有样本同时参加运算,因此批量方式的学习速度往往远优于串行方式。
单样本训练遵循的是只顾眼前的本位主义,只针对每个样本产生的误差训练,难免顾此失彼,使得整个训练次数增加,导致收敛速度过慢。批量训练:
BP神经网络的优点:
- 非线性映射能力
- 泛化能力
- 容错能力 允许输入样本中带有较大误差甚至个别错误。反应正确规律的知识来自全体样本,个别样本中的误差不能左右对权矩阵的调整。
BP神经网络的局限性:
梯度下降法的缺陷:
- 目标函数必须可微;
- 如果一片区域比较平坦会花费较多时间进行训练;
- 可能会陷入局部极小值,而没有到达全局最小值;(求全局极小值的目的是为了实现误差的最小值)
BP神经网络的缺陷:
- 需要的参数过多,而且参数的选择没有有效的方法。确定一个BP神经网络需要知道:网络的层数、每一层神经元的个数和权值。权值可以通过学习得到,如果,隐层神经元数量太多会引起过学习,如果隐层神经元个数太少会引起欠学习。此外学习率的选择也是需要考虑。目前来说,对于参数的确定缺少一个简单有效的方法,所以导致算法很不稳定;
- 属于监督学习,对于样本有较大依赖性,网络学习的逼近和推广能力与样本有很大关系,如果样本集合代表性差,样本矛盾多,存在冗余样本,网络就很难达到预期的性能;
- 由于权值是随机给定的,所以BP神经网络具有不可重现性;
梯度下降法(最速下降法的改进):
针对算法的不足出现了几种BP算法的改进。
- 动量法
动量法是在标准BP算法的权值更新阶段引入动量因子α(0<α<1),使权值修正具有一定惯性,可以看出,在原有的权值调整公式中,加入了动量因子以及上一次的权值改变量。加入的动量项表示本次权值的更新方向和幅度,不但与本次计算所得的梯度有关,还与上一次更新的方向和幅度有关。动量项反映了以前积累的调整经验,对于t时刻的调整起到了阻尼作用。当误差曲面出现骤然起伏时,可减小震荡趋势,提高训练速度。
- 调节学习率法
在平缓区域希望学习率大一点减小迭代次数,在坑凹处希望学习率小一点,较小震荡。所以,为了加速收敛过程,希望自适应改变学习率,在该大的时候大,在该小的时候小。
学习率可变的BP算法是通过观察误差的增减来判断的,当误差以减小的方式区域目标时,说明修正方向是正确的,可以增加学习率;当误差增加超过一定范围时,说明前一步修正进行的不正确,应减小步长,并撤销前一步修正过程。学习率的增减通过乘以一个增量/减量因子实现:
误差曲面上存在着平坦区域,权值调整进入平坦去的原因是神经元输出进入了转移函数的饱和区,如果在调整净土平坦区后,设法压缩神经元的净输入,使其输出退出转移函数的饱和区,就可以改变误差函数的形状,从而使调整脱离平坦区,实现这一思路的具体做法是在原转移函数中引入一个陡度因子:
![]()
当发现关于E的偏导接近0而E仍然比较大是,可以判断已经进入了平坦区,此时令陡度影子大于1,当退出了平坦区后,再令陡度因子等于1,当陡度因子大于1时,坐标轴压缩了陡度因子倍,神经元的函数曲线的敏感区变长,从而使得绝对值较大的netk退出饱和值。该方法对于提高BP算法的收敛速度十分有效。
BP神经网络的设计:
BP神经网络采用有监督学习。解决具体问题时,首先需要一个训练集。然后神经网络的设计主要包括网络层数、输入层节点数、隐层节点数、输出层节点数、以及传输函数、训练方法、训练参数。
(一)输入输出数据的预处理:尺度变换。尺度变化也称为归一化或者标准化,是指变换处理将网络的输入、输出数据限制在[0,1]或者[-1,1]区间内。进行变换的原因是,(1)网络的各个输入数据常常具有不同的物理意义和不同的量纲。尺度变换使所有分量都在一个区间内变化,从而使网络训练一开始就给各输入分量以同等重要的地位;(2)BP神经网络神经元均采用sigmoid函数,变换后可防止因净输入的绝对值过大而使神经元输出饱和,继而使权值调整进入误差曲面的平坦区;(3)sigmoid函数输出在区间[0,1]或者[-1,1]内,如果不对期望输出数据进行变换处理,势必使数值大的分量绝对误差大,数值小的分量绝对误差小。
(二)神经网络结构设计
1)网络层数 BP神经网络最多只需要俩个隐层,在设计的时候一般先只考虑设一个隐层,当一个隐层的节点数很多但是依然不能改善网络情况时,才考虑增加一个隐层。经验表明,如果在第一个隐层较多的节点数,第二个隐层较少的节点数,可以改善网络性能。
2)输入层节点数 输入层节点数取决于输入向量的维数。应用神经网络解决实际问题时,首先应从问题中提炼出一个抽象模型。如果输入的是64*64的图像,则输入向量应为图像中左右的像素形成的4096维向量。如果待解决的问题是二院函数拟合,则输入向量应为二维向量。
3)隐层节点数设计 隐含节点数对BP神经网络的性能有很大影响,一般较多的隐含层节点数可以带来更好的性能,但是导致训练时间过长。通常是采用经验公式给出估计值:
4)输出层神经元个数
5)传递函数的选择 一般隐层选择sigmoid函数,输出层选择线性函数。如果也使用sigmoid函数,则输出值将会被限制在(0,1)或者(-1,1)之间。
6)训练方法的选择 一般来说,对于包含数百个权值的函数逼近网络,使用LM算法收敛速度最快,均方误差也小,但是LM算法对于模式识别相关问题的处理能力较弱,且需要较大的存储空间。对于模式识别问题,使用RPROP算法能收到较好的效果。SCG算法对于模式识别和函数逼近都有较好的性能表现。串行方式需要更小的存储空间,且输入样本具有一定随机性,可以避免陷入局部最优。批量方式的误差收敛条件非常简单,训练速度快。
7)初始权值的确定 BP网络采用迭代更新的方式确定权值,因此需要一个初始值,一般初始值都是随机确定的,这容易造成网络的不可重现性,初始值过大过小都会对性能造成巨大影响,通常将初始权值定义为较小的非零随机值,经验值为:其中F为权值输入端连接的神经元个数。
![]()
Python实现BP神经网络
1 #! /usr/bin/env python 2 # -*- coding:utf-8 -*- 3 import random 4 import numpy as np 5 from tensorflow.examples.tutorials.mnist import input_data 6 # 下载mnist数据集 7 mnist = input_data.read_data_sets('/tmp/', one_hot=True) 8 9 10 class BpNetwork(object): 11 12 def __init__(self, sizes): 13 """ 14 The list 'sizes' contains the number of neurons in the respective 15 layers of the network. For example,if the list was [2, 3, 1] then 16 it would be a three-layer network, with the first layer containing 17 2 layer, the second layer 3 neurons and the third layer 1 neuron. 18 The bases and weights for network are initialized randomly, using a 19 Gaussian distribution with mean 0 and variance 1. 20 Note that the first layer is assumed to be an input layer, and by 21 convention we won't set any biases for those neurons, since biases 22 only ever used in computing the outputs from later layers. 23 :param sizes: list contains the number of neurons in every layer. 24 """ 25 self.num_layers = len(sizes) 26 self.sizes = sizes 27 self.biases = [np.random.randn(y, 1) for y in sizes[1:]] 28 self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] 29 30 def feed_forward(self, a): 31 """ 32 Return the output of the network if 'a' is input 33 """ 34 for b, w in zip(self.biases, self.weights): 35 a = sigmoid(np.dot(w, a) + b) 36 return a 37 38 def stochastic_gradient_descent(self, training_data, epochs, mini_batch_size, eta, test_data=None): 39 """ 40 Train the neural network using mini-batch stochastic gradient descent. 41 :param training_data: a list of tuples '(x,y)' x representing the training input 42 y representing the desired output 43 :param epochs: 44 :param mini_batch_size: 45 :param eta: learning rate 46 :param test_data: if 'test_data' is provided then the network will be evaluated 47 against the test data after each epoch, and progress printed out. 48 :return: 49 """ 50 n = len(training_data) 51 for j in range(epochs): 52 random.shuffle(training_data) 53 mini_batches = [ 54 training_data[k:k+mini_batch_size] 55 for k in rang(0, n, mini_batch_size)] 56 for mini_batch in mini_batches: 57 self.update_mini_batch(mini_batch, eta) 58 if test_data: 59 print("Epoch {0}: {1} / {2}".format(j, self.evaluate(test_data), len(test_data))) 60 else: 61 print("Epoch {0} complete".format(j)) 62 63 def update_mini_batch(self, mini_batch, eta): 64 """Update the network's weights and biases by applying gradient descent 65 using back propagation to a single mini batch. 66 :parameter mini_batch: is a list of tuple "(x,y)" , 67 :parameter eta: learning rate""" 68 nabla_b = [np.zeros(b.shape) for b in self.biases] 69 nabla_w = [np.zeros(w.shape) for w in self.weights] 70 for x, y in mini_batch: 71 delta_nabla_b, delta_nabla_w = self.backprop(x, y) 72 nabla_b = [nb + dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] 73 nabla_w = [nw + dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] 74 self.weights = [w - (eta/len(mini_batch))*nw for w,nw in zip(self.weights, nabla_wa)] 75 self.biases = [b - (eta/len(mini_batch))*nb for b, nb in zip(self.biases, nable_b)] 76 77 def back_prop(self, x, y): 78 """ 79 :param x: training data 80 :param y: desired output target 81 :return: a tuple "(nabla_b, nabla_w)" representing the gradient for the 82 cost function. 83 """ 84 nabla_b = [np.zeros(b.shape) for b in self.biases] 85 nabla_w = [np.zeros(w.shape) for w in self.weights] 86 activation = x 87 activations = [x] # list to store all the output values 88 zs = [] # list to store all the z vectors 89 for b, w in zip(self.biases, self.weights): 90 z = np.dot(w, activation) + b 91 zs.apppend(z) 92 activation = sigmoid(z) 93 activations.append(activation) 94 delta = self.cost_derivative(activations[-1], y) * sigmoid_prime(zs[-1]) 95 nabla_b[-1] = delta 96 nabla_w[-1] = np.dot(delta, activations[-2].T) 97 for l in range(2, self.num_layers): 98 z = zs[-l] 99 sp = sigmoid_prime(z) 100 delta = np.dot(self.weights[-l + 1].T, delta) * sp 101 nabla_b[-l] = delta 102 nabla_w[-l] = np.dot(delta, activations[-l-1].T) 103 return nabla_b, nabla_w 104 105 def evaluate(self, test_data): 106 """ 107 :param test_data: 108 :return: return the number of test inputs for which the neural output is the 109 correct result. 110 """ 111 test_results = [(np.argmax(self.feed_forward(x)), y) 112 for (x, y) in test_data] 113 return sum(int(x == y) for (x, y) in test_results) 114 115 @staticmethod 116 def cost_derivative( output_activations, y): 117 """ 118 :param output_activations: 119 :param y: 120 :return: Return the vector of partial derivatives for the output activations. 121 """ 122 return output_activations - y 123 124 125 def sigmoid(x): 126 """The sigmoid function.""" 127 return 1.0 / (1.0 + np.exp(-x)) 128 129 130 def sigmoid_prime(x): 131 """Derivative of the sigmoid function.""" 132 return sigmoid(x) * (1 - sigmoid(x)) 133 134 135 training_data, validation_data, test_data = mnist.train, mnist.validation, mnist.test 136 net = BpNetwork([784, 30, 10]) 137 net.stochastic_gradient_descent(training_data, 30, 10, 3, test_data=test_data)
上面代码中不仅给出了BP神经网络代码,还运用代码处理了mnist数据集。