Logistic回归(逻辑回归)进行分类的主要思想:根据现有数据对分类边界线建立回归公式,以此进行分类。
知乎上的简述:
该算法可根据已知的一系列因变量估计离散数值(比方说二进制数值 0 或 1 ,是或否,真或假)。简单来说,它通过将数据拟合进一个逻辑函数来预估一个事件出现的概率。因此,它也被叫做逻辑回归。因为它预估的是概率,所以它的输出值大小在 0 和 1 之间(正如所预计的一样)。
让我们再次通过一个简单的例子来理解这个算法。
假设你的朋友让你解开一个谜题。这只会有两个结果:你解开了或是你没有解开。想象你要解答很多道题来找出你所擅长的主题。这个研究的结果就会像是这样:假设题目是一道十年级的三角函数题,你有 70%的可能会解开这道题。然而,若题目是个五年级的历史题,你只有30%的可能性回答正确。这就是逻辑回归能提供给你的信息。
从数学上看,在结果中,几率的对数使用的是预测变量的线性组合模型。
最终得到的结果:X轴作为特征值输入,Y轴获得数据属于 某个类型的概率。

Sigmoid函数: y = 1 / (1 + e -x) ,记为: f(z) = 1 / (1 + e -z)
我们 可以 在 每个 特征 上乘 以 一个 回归 系数, 然后 把 所有 的 结果 值 相加, 将 这个 总和 代入 Sigmoid 函数 中, 进而 得到 一个 范围 在 0~ 1 之间 的 数值。 最后, 结果 大于 0. 5 的 数据 被 归入 1 类, 小于 0. 5 的 即被 归入 0 类。 所以, Logistic 回归 也可以 被 看成 是一 种 概率 估计。
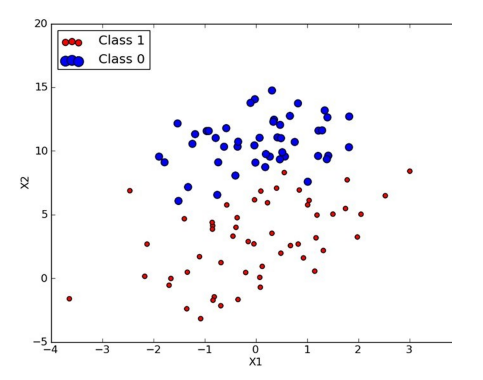
问题的第一次转化:
Z = h(x) = w0 + w1x1 + w2x2 + ......wnxn ,这个函数,又叫假设函数。 (如上图,class1或class2相当于不同的 f(z)值,0或1;而X,Y相当于特征值,X0 或 X1)
上述公式中的W为参数,也称为权重,可以理解为x1和x2对Z的影响度。对这个公式稍作变化就是:
Z = h(x) = WTX
假如, 求得的 W 是最佳,那么,这些W值,应该符合以下特性:
dZ= j(W) = 1/2 *[ (Z0 - h0)2 + (Z1 - h1)2 + ....(Zn - hn)2] = 1/ 2 * ∑n i=1 (Zi - hi) , Zn是指 第n个样本,已知类型的真值,hn 用假设函数求出第n个样本的 类型的近似值。
这里的这个损失函数就是著名的最小二乘损失函数
(化简后,就可以得到测量平差中的 V = Bw - l ,矩阵形式的函数方程组了)
问题的第二次转化:http://www.cnblogs.com/NeilZhang/p/8454890.html
为求得最优的W值,使损失函数 f(W)取最小值。
解决思路一: 一般来说,只要判断j''(W)< 0,那么 j'(W) = 0 时,j(W)具有最小值,获得的W矩阵解,就为最佳的W参数组了。 (需要一次将所有数据堆到矩阵中,受限于计算机内存)
解决思路二:使用梯度上升/ 下降方法,来寻找最佳参数。
(在最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数,和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。)
摘自网络:https://www.cnblogs.com/pinard/p/5970503.html
梯度下降法和最小二乘法相比,梯度下降法需要选择步长,而最小二乘法不需要。梯度下降法是迭代求解,最小二乘法是计算解析解。如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。但是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。
摘自网络:https://www.cnblogs.com/pinard/p/5970503.html(要点)
在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。对于在点(x0,y0)的具体梯度向量就是(∂f/∂x0, ∂f/∂y0)T.或者▽f(x0,y0),如果是3个参数的向量梯度,就是(∂f/∂x, ∂f/∂y,∂f/∂z)T,以此类推。
那么这个梯度向量求出来有什么意义呢?他的意义从几何意义上讲,就是函数变化增加最快的地方。具体来说,对于函数f(x,y),在点(x0,y0),沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。或者说,沿着梯度向量的方向,更加容易找到函数的最大值。反过来说,沿着梯度向量相反的方向,也就是 -(∂f/∂x0, ∂f/∂y0)T的方向,梯度减少最快,也就是更加容易找到函数的最小值。
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了山脚。当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山峰低处。
梯度下降算法大概的思路是:我们首先随便给W一个初始化的值,然后改变W值让j(W)的取值变小,不断重复改变W使j(W)变小的过程直至j(W)约等于最小值。
首先我们给W一个初始值,然后向着让j(W)变化最大的方向更新W的取值,如此迭代。公式如下:
W = W - a * ∂j(W) / ∂W (对f(W)进行求W偏导,复合函数求导)
化简,第j次迭代:
W = W - a * (Zi-h(Xi)) * Xi
展开式:
[w0,w1,w2....]T = [w0,w1,w2....]T - a * (Zi - [w0,w1,w2....]T * [xi0,xi1,..........]) *[xi0,xi1,..........]T i为第i个样本, a为步长;
如果数据不止一个,那么:
[w0,w1,w2....]T = [w0,w1,w2....]T - a * ∑n i=1 ( (Zi - [w0,w1,w2....])T * [xi0,xi1,..........]) * [xi0,xi1,..........]T )
注意: 为了让矩阵计算顺利,让Xm0 = 1
使用批量梯度上升算法求W,在样本不多的情况下
for j in R
W = W + a *XT (Z-H)
W(1*n) = [w0,w1,w2....wn]T
X(m*n) = [ x00, x01.....x0n
x10, x11.....x0n
xm0, x11.....xmn]
Z(m*1) = [Z0,Z1,Z2,... Zm]T
H(m*1) = W T X
使用随机梯度上升求W,在样本 很多的情况下:
for i in 样本:
W = W + a *XT (Z-H)
W(1*n) = [w0,w1,w2....wn]T
X(1*n) = [ xi0, xi1.....xin]
Z = Zi
H = WT X
*不必一次将所有学习数据堆到一个矩阵中,不受内存限制。
最小化误差
反过来就是最大化
而
拆开来就是:
到这就可以用梯度上升算法了,对
因此更新回归系数的公式就是:
这就是书中章节的梯度上升算法的一个推导过程。我感觉在从这里面可以看出梯度上升算法和梯度下降算法分别是用来求最大值和最小值,也许仅仅使一个负号的差别。