微分:
图像一:f是里程,t是时间,如果v是一定时,那么不难理解,f的图像是一条固定斜率的直线;
图像二:基于图一,v和t的图像,是一条平行于t轴的直线;并且,在t1处,f = v * t1;
图像三:如果v是随t的变化而变化,那么如果有v = c t;那么,在t1处,有 f = 1 / 2 * c * t1 * t1;
图像四:基于图三,f是一条凹抛物线;
问题一:如何知道,在任意的t1处,根据f的图像,求得v的值。也就是根据f的表达式,求得任意时刻的v?
假设,在t1处,有f(t1);在t1 + △t处,有f(t1 + △t),那么, t1 ~ t1+△t的平均速度 = [f(t1 + △t) - f(t1)] / △t = 1 / 2 * c * ( 2*t1 + △t )
那么,当△t 无限接近0的时候,得到的就是t1的速度,v(t1) = c *t1;如果△t 不是接近0,得到的就是平均速度。
所以,要学习微分,先学习求极限;对所有的导数推导,如sinx,e^x的推导,也可以这样推;
思考:matlab求某个x处的导数(斜率),是不是也是用极小的△x来代入[f(x+△x) - f(x)] / △x的呢?
利用导数,可以找出函数的特殊点:
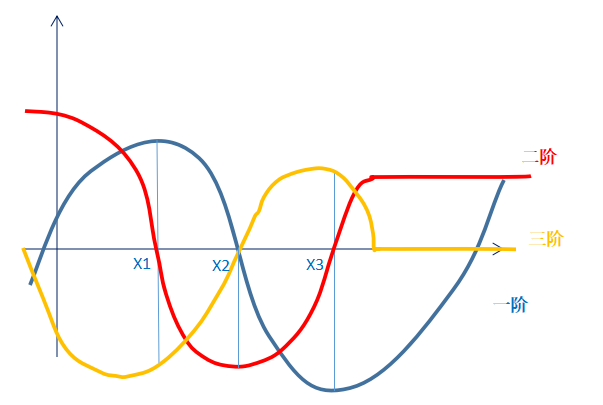
1. 当二阶导数为0时,x1 = x3 = 0,那么原函数处于凸顶或者凹底;
2. 当三阶导数,在x1< 0时,原函数处于凸顶(二阶函数的变化速度为负,原函数往负方向拐);
3. 当三阶导数,在x2 = 0时,证明二阶导数在x2处,速度绝对值已经最大(接下来就下降);那么,证明原函数,其上升或下降的速度已经减缓,在不久就触底了。
有关指数函数 :
y = ex;
y' = ex;
如果有一函数:y = y'
y = 1,y' = 1
有矛盾,y = 1 + x 时,才有 y' = 1;
有矛盾,y' = 1 + x 为必须符合条件;
有矛盾,y = 1+ x + 1/2 * x2 上面才成立;
有矛盾,y' =1+ x + 1/2 * x2 为必须符合的条件;
有矛盾,y = 1 + x + 1/2 * x2 + 1 / (2*3) *x3上面才成立
。。。
直到 y = e^x 的无穷泰勒级数展开才行。
e到底有何特别呢?
假如银行存一年,给100%利息,1~n年后,利叠利1,2,4,8...
如果利息按月计算,那么每月利息是本金的1/12,1~12月的本金+利息为:
(1+1/12),(1+1/12)^2……(1+1/12)^12 > 2
那如果利息按天计算,1~365天,本金+利息为:
(1+1/365)^365>(1+1/12)^12 > 2
但是:
(1+1/n)^n <= e
积分
假设每一个步长记录一次y的值,假设步长△x =1,那么:
y = 0,1,4,9,16……
斜率:
s = (1-0)/△x ,(4-1)/△x ,(9-4)/△x……
即:
s = 1,3,5,7……
那么,由s求回y,就是对s的值进行累加。
进入代数:
y:y0,y1……yn;
△y:y1-y0,y2-y1,y3-y2……y(n)-y(n-1)
Σ△y = y(n)-y(0)
那么,有:
Σ [(△y / △x)* △x ] =( y(n) - y(0) )
如果让△y和△x足够小,趋近于0的称为dy,dx,而且Σ也不太合适,所以写成:
∫(dy/dx)dx = ( y(n) - y(0) )
(*始终记住一点,∫代表连加,积分就是,微小量乘以斜率,然后连加)
用求极限的方式:
已知y'(x),在区间(x1,x2)中,△x = (x1-x2 )/ n
当n足够大,又有y'(x1),y'(x1+△x),y'(x1+2△x)……y'(x2)就可以近似计算数值y(x2)-y(x1)
求导法则:
1. 函数相乘 p(x)=f(x)g(x) dp/dx = f(x) * dg / dx + g(x) * df / dx;
例子:p(x) = x2 * x dp/dx = x2 * 1 + x * 2x = 3x2
来由:
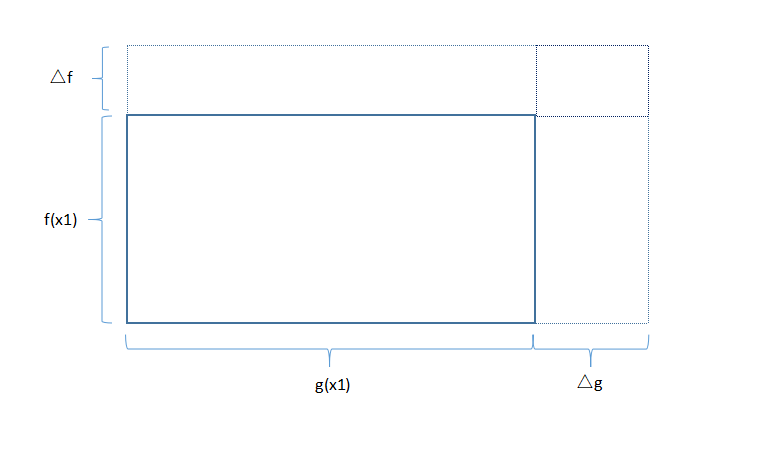
想象一下,f(x)和g(x)分别是长方形的长和宽,x0处,有p(x0)这个面积。
那么,移动一点点,△x,那么对于f(x),有△f,对于g(x),有△g;
那么,面积△p = f(x0) * △g + g(x0) * △f + △g * △f
从而 △p / △x = f(x0) * △g / △x + g(x0) * △f / △x + △g * △f / △x
那么,当△x无限小,△g * △f / △x 变为0 ,△x无限小用dx表示,△p、 △g、△f用dp、dg、df表示。
2. 函数嵌套p(x) = f(g(x)) dp/dx = df/dg * dg/dx
例子:p(x) = f(x)n dp/dx = n *f(x)(n-1) * df/dx
例子:p(x) = sin(3x) dp/dx = 3 * cos(3x) ,周期缩短了3陪,但是最大值一样,那斜率自然增大3倍。
洛必达法则:
当x趋近于0时,f(x)、g(x)也趋近于0
f(x)/g(x) = (△f /△x ) / (△g /△x )
反函数:
y = f(x) 和 x = f -1(y);
指数函数的逆函数:
f(x) = ex x = loge f(x) = ln(f(x))
f(x) = cx x = logc(f(x))
yY = exeX=ex+X
ln(yY) = ln(ex+X) = x + X = lny + lnY
ln(y2) = x + x =2x = 2lny ln(yn)=n * lny
反函数求导
例子:
y = ax + b = f(x)
x = f -1(x) = (y - b) / a (逆过程就是乘法变除法,加法变减法,且顺序相反)
y = ex lny = x 求导:x' = d(lny) / dy * dy / dx = 1 已知 dy / dx =ex 那么d (lny) / dy = 1 / ex
所以 (lny)' = 1 / y
y = sin(x) x = sin-1(y) = arcsin(y)
y = sin (sin-1(y))
两边对y求导:
1 = cos(sin-1(y)) * dsin-1(y) / dy = cosθ * dsin-1(y) / dy
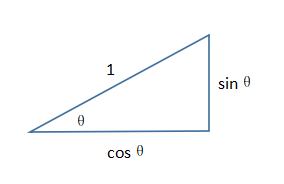
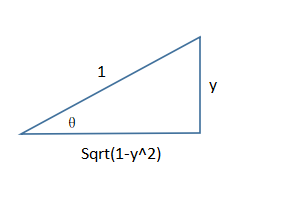
cosθ = Sqrt(1 - y 2)
所以:
dsin-1(y) / dy = 1 / Sqrt(1 - y 2)
已知 f'(a) 的值,也已知x的值,求f(x)
当x接近a的时候,有: df / dx = f '(a) ≈ [ f(x) - f(a) ] / ( x - a )
f(x) ≈ f(a) + ( x - a ) * f ' (a) (1)
已知 F(x) = 0,求 x: x - a ≈ - F(a) / F ' (a) (2)
例子:
求Sqrt(9.06)的值。f(x) = x1/2 f ' = 1 / 2 * x-1/2
那么,可以选择 a = 9 f(a) = 3 f '( a) = 1 / 6
由(1)式得:
f(9.06) = 3 + 0.06 * 1 / 6 = 3.01
图像:
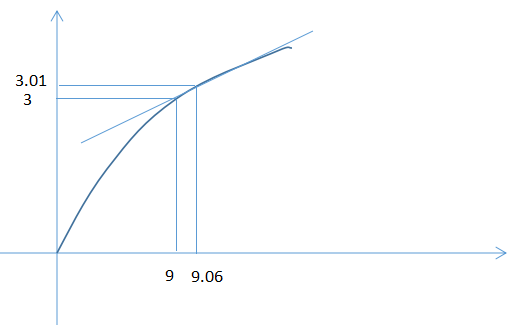
还可以:
F(x) = x2 - 9.06 = 0 求x的解
令 a = 3
F(a) = 9 - 9.06 = -0.06
F'(a) = 2a = 6
根据(2)式子
x - 3 = - 0.06 / 6 = 0.01 x = 3.01
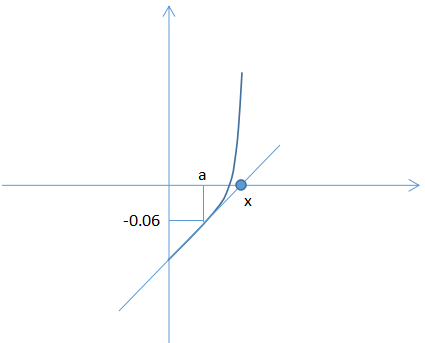
所以,可以继续使得
a = 3.01 F(a) = 0.0001 F'(a) = 2a = 6.02 x = ???
直到 x - a 的值接近0;
这就是牛顿法了
f(x) = f(x0 + △x)
f(x0 + △x) = f(x0) + ∫ f '(x) dx 积分区间(x0,x0 + △x)
*还记得速度的积分(从0~t1),就是t1处的里程吗?(三角形面积值,是f(t1)值)
*再解析浅一点,从0~t1积分,就是f(t1);从0~t2积分,就是f(t2);从t1~t2,就是△f = f(t2) - f(t1);(梯形面积,也就是两f(t1)、f(t2)值相减)
*从x0 ~ x0 + △x,就是△f = f(x0 + △x) - f(x0 );
所以:f(x0 + △x) = f(x0) + ∫ f '(x) dx 积分区间(x0,x0 + △x)
而 f '(x) = ∫ f ''(x) dx + f '(x0)
代入得:f(x0 + △x) = ∫ (∫ f ''(x) dx + f '(x0)) dx + f(x0)
其中
∫ (∫ f ''(x) dx + f '(x0)) dx = ∫ (∫ f ''(x) dx)dx + ∫ f '(x0) dx
其中
∫ f '(x0) dx = f '(x0) * △x = f '(x0) (x - x0) 对一个常数 f '(x0)进行积分,就是求矩形面积
其中
∫ (∫ f ''(x) dx)dx , f ''(x) = ∫ f '''(x) dx + f ''(x0),代入∫ (∫ (∫ f '''(x) dx + f ''(x0)) dx)dx
其中 ∫ (∫ f ''(x0) dx)dx ,将f ''(x0) 视为常数, ∫ f ''(x0) dx = f ''(x0) (x - x0)
代入得 ∫ f ''(x0) (x - x0) dx = (x - x0) 2/ 2 * f ''(x0)
至此,f(x) = f(x0 + △x) = f(x0) + f '(x0) (x - x0) + (x - x0) 2/ 2 * f ''(x0) + ∫ ∫ ∫ f '''(x) dx dxdx
对∫ ∫ ∫ f '''(x) dxdxdx 再次分解
∫ ∫ ∫ [ f '''(x0) + ∫ f ''''(x)dx ]dxdxdx = ∫ ∫ ∫ f '''(x0)dxdxdx + ∫ ∫ ∫ ∫ f ''''(x)dxdxdxdx
∫ ∫ ∫ f '''(x0)dxdxdx = f '''(x0) * ∫ ∫ ( x - x0)dxdx = f '''(x0) * ∫ ( x - x0)2 / 2 dx = f '''(x0) * ( x - x0)3 / ( 3 * 2)
至此,f(x) = f(x0 + △x) = f(x0) + f '(x0) (x - x0) + (x - x0) 2/ 2 * f ''(x0) + f '''(x0) * ( x - x0)3 / ( 3 * 2) + ∫ ∫ ∫ ∫ f ''''(x)dxdxdxdx
也可以从另一个思想推导泰勒公式:
比如有一个函数,f(x) ,我们要仿造一个函数 g(x) ,在X0附近, 要无限接近f(x)。那我们就可以,预测X0附近的 f(x) 的值了,非常好!
那么,假设f(x)能求n阶导数,n可以是任意的,其最终大小视f(x)而定,需要有:
f(X0) = g(X0)
f '(X0) = g '(X0)
f ''(X0) = g ''(X0)
……
f n(X0) = g n(X0)
那么,可以猜想,g(x)又可以求高阶层导数,会不会是:
g(x) = a0 + a1x + a2x2 + a3x3 +a4x4 + ……anxn
例子:
拿cosX,在X = 0处的近似:
求一阶:
原曲线: f(x) = cosx
仿曲线:f(x) ≈ g(x) = a0 + a1x
满足:
f(0) = g(0)
f '(0) = g '(0)
解得 g(x) = 1
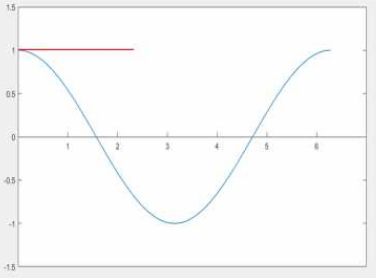
仅仅是一条直线,在x = 0附近,一点都不像,g(x)只有在X=0处能近似f(x)。
继续,求二阶:
仿曲线:f(x) ≈ g(x) = a0 + a1x + a2x2
满足:
f(0) = g(0)
f '(0) = g '(0)
f ''(0) = g ''(0)
解得:g(x) = 1 - 1 / 2 x2
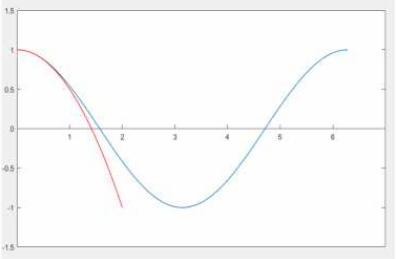
很好,在x = 0附近已经可以近似用 g(x)代替了。只要x离开x = 0不远,可以用g(x)代替。并且可以看出,对于其他的x = Xn,只要解出属于Xn的各个a0 , a1 , a2 就可以模拟Xn附近的函数值了。
这是一个非常重要的信息,只要离x = Xn足够近,只要解出属于Xn的各个a0 , a1 , a2,甚至不需要求很高阶,亦可以满足要求g(x) 无限接近 f(x)。
如果我们继续,求三阶:
仿曲线:f(x) ≈ g(x) = a0 + a1x + a2x2+ a3x3
满足:
f(0) = g(0)
f '(0) = g '(0)
f ''(0) = g ''(0)
f '''(0) = g '''(0)
解得:g(x) = 1 - 1 / 2 x2 + 1 / 2 x4

至此,我们有理由相信,只要仿曲线g(x)的阶数够高,无论x离 x = 0多远都好,也就是任意的x = Xn,都能满足g(x)无限接近f(x)。
.
..
...
那猜想一下,泰勒公式的通式:
f(x) ≈ g(x) = f(0) + f1(0) / 1! *x + f2(0) / 2! *x2 + ……+ fn(0) / n! xn
因为
g(0) = f(0) ,
gn(0) = fn(0) , 这里比较考究,因为求导第n阶导数的时候,前面的各项已经被消为0了。而对xn 的各阶求导,剩下n! 这个乘数,最终要留下fn(0),那么an只能等于fn(0) / n! 。
.
..
...
前面提及,如果我不想在x = 0处研究泰勒公式,要想在x = X0 处研究,那么,自然各个fn(0)得替换为fn(X0)。这样的好处,上面提及了,可以不用展开那么多项;
其次,原公式中,各个x项,是相对于x = 0的,也就是x = x - 0,那现在替换为 x = x - X0
那么,在x = X0 附近的泰勒展开式:f(x) ≈ g(x) = f(X0) + f1(X0) / 1! *(x - X0) + f2(X0) / 2! *(x - X0)2 + ……+ fn(X0) / n! *(x - X0)n
.
..
...
泰勒公式,还可以用来线性化函数
例如:
f(x,y) = a x2y
想要在(X0,Y0)附近,求近似g(x, y)
一阶:
f(x,y) ≈ g(x, y) = f(X0,Y0) + df '(X0,Y0) / dx * (x - X0) + df '(X0,Y0) / dy * (y - y0)
二阶:
f(x,y) ≈ g(x, y) = 一阶 + df ''(X0,Y0) / dxdx / 2! * (x - X0)2 + df ''(X0,Y0) / dydy / 2! * (y - Y0)2 + df ''(X0,Y0) / dxdy / 2! * (x - X0) (y - Y0) + df ''(X0,Y0) / dydx / 2! * (x - X0) (y - Y0)
*df '(X0,Y0) / dx 的意思是,f(x,y)对x求偏导,然后,代入(X0,Y0)
当 x0 = 0 , △x = X 时
对于
sin(x) = x - x3 / 3!+ x5 / 5!+……
cos(x) = 1 - 1/2! * x2 + 1/ 4! * x3 +……
对于泰勒公式用于指数函数,得出欧拉公式:
eix = 1 + ix + 1/2! (ix)2 + 1/3! (ix)3+……
= (1 - 1/2! * x2 + 1/ 4! * x3 +……)+ i *(x - x3 / 3!+ x5 / 5!+……)
= cosx + i sinx
图像:
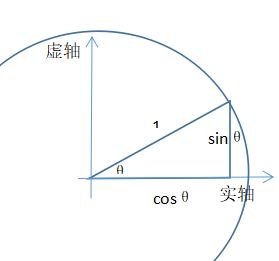
*欧拉公式是傅里叶变换的基础
此式子能解析所有的振动:m * d2y / dt2 + 2 * r * dy / dt + k * y = 0 或 my'' + 2ry' + ky = 0
对于这个方程,要使得其成立的条件,有如下两种情况:
情况一: d2y / dt2 =0
那么可以有 y = c + dt
情况二:m = 0, dy / dt = ay, a = - k / 2r
dy / dt = ay 可以有 y = eat
情况三:r = 0,w2 = k/m , d2y / dt2 = - w2y
d2y / dt2 = - w2y 可以有 y = cos(wt) 或 y = sin(wt) 或 y = c* cos(wt) + d*sint(wt)(通解)
例子一:

物体的重力为m,弹簧的弹力系数是k(每拉长一段距离,就产生多少力)
以向下的距离为正,距离为y(即弹簧自然状态时,y为0)
那么:加速度就是 y''(t) = d2y / dt2
从而, 有 - k y = m * d2y / dt2 (质量成加速度就是力,由于弹力总是和物体的力方向相反,所以左边加上负号)
*r代表空气阻力系数
例子二:
y = eλt
代入公式:
mλ2eλt + 2 r λ eλt + k eλt = 0 化简后得:mλ2+2 r λ + k = 0
r = ± Sqrt(r2 - km) / m
使 m =1 , r = 3 , k = 8 ,解得 λ = -2 , -4, 那么通解 y(t) = Ce-2t + De-4t
例子三:
当m = 1, r = 3, k = 10时,解得 λ = -3 ± i ,是虚数y(t) =Ce(-3+i)t + De(-3-i)t
如果使用欧拉公式,那么:
eit = cos(t) + i * sin(t)
e-it = cos(t) - i * sin(t)
y(t) = A*e-3tcos(t) + B *e-3t *sin(t)
用人话来说,就是y随着时间的改变,其振动的幅度逐渐降低,直到y回到正常的范围值
例子四:
当m = 1, r = 3, k = 10时,解得 λ1 = λ2 = -3
y = y(t) =Ce-3t + De-3t
OK,结论就是:形如 my'' + 2ry' + ky = 0 的线性常系数微分方程,可以通过引入y = eλt 来解决,通过求取λ,符合以上三种情况
式子一: dy/dt = cy y(0) = ... y(t) = y(0) * ect
式子二: dy / dt = cy + s
这个模型可以表示银行存款,c表示利率,s可以表示每次持续存入的额外数额
dy / dt = c ( y + s / c )
d( y + s / c ) / dt = c ( y + s / c)
因为 dy / dt = cy + s
d( y + s / c ) / dt = d( y + s / c ) / dy * dy / dt = c ( y + s / c)
那么,可以看出,dy / dt = c ( y + s / c ),其实是从 (0 , y(0) + s / c )为起点的
结论:
y(t) + s / c = (y(0) + s / c) ect (对应于式子一)
以上说了这么多,就是说,t 时刻 y 的增长速度(dy / dt),受t时刻的状态 y(t) 的影响,所以有各种:
dy / dt = cy + s各式。
应用例子一:
假如有人口方程 p(t) , 那么应该用什么样的微分方程,描述人口增长比较合理?
首先,我们不直接猜想P(t) , 而是P'(t) ,这很重要,也是中心思想。解决这类问题,从猜想其变化速度入手。
dP / dt = cP - sP2, c表示出生率(速度受到出生率的影响),s表示衰减因子(因为可能人太多,出现竞态)导致速度下降。
情况一:dP / dt = 0,表示人口永远不增长,人口保持稳定(或者在某个时刻t,速度变为0)
P = c / s(100亿?)
情况二:P'(0) = A, 表示我们根据历史数据,从计算的时刻t = 0开始,有一个初始速度。
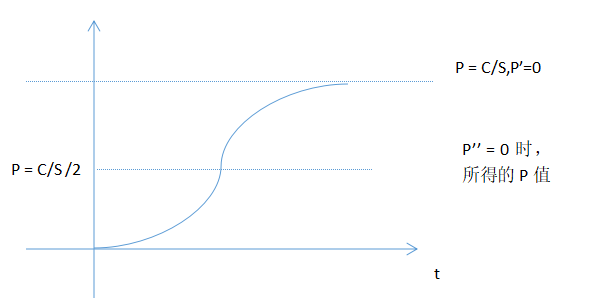
那么,如何求解出P??
方法一:
令 y(t) = 1 / P(t)
那么 dy / dt = -1 / P2(t) * dP/ dt = (cP - sP2) / P2 = s - c / p = s - cy(跟上面提到的式子非常相似)
y(t) - s / c = ( y(0) - s / c ) e-ct
那将y(t)代回,即可得出P(t) ;
*函数在下一刻的速率,受到函数当前的值的影响,必须考虑函数本身就是 y = a * ecx + b 的形式
*这个价值在于,变化的速度,最终的稳定值,会根据自身值调整
应用例子二:
有关捕食者和猎物的关系:猎物不够,捕食者自然减少;捕食者减少,猎物又会自动补充。
捕食者的增长速度:du / dt = - c u + s * u * v ; - c u 表示猎物减少的情况
猎物的增长速度:dv / dt = c v - s * u * v;
记住,六个最基本的导数:
xn nxn-1
sin x cos x
cos x -sin x
ecx cecx
lnx 1/x
二重积分的几何解析
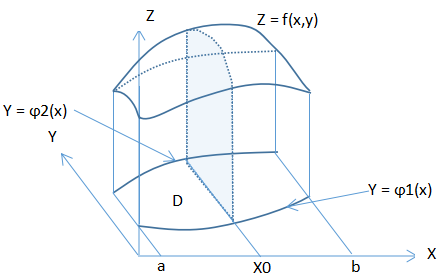
首先,二重积分就是求不规则立方体的体积
V = ∫∫D f(x,y) dx dy
显然,仅仅靠已知f(x, y)和一个符号D是求不到的
所以,D应该有一个范围
D = { (x,y) | a <= x <= b && φ1(x) <= y <= φ2(x)} 意思是,D是x,y平面的一个封闭范围
直观告诉我,体积 = 底面积 * 高
那以X轴方向看过去,以蓝色部分为底面。
1. 先解决底面面积 S :
在X0处,Z = f (X0, y), 如果蓝色部分是矩形的话,也就是X是定值,那么只需要 S = Z * (φ2(x0) - φ1(x0))即可。
但是,由与Z是函数,那么,所以 S = ∫ f(x0,y) dy ,积分区间(φ2(x0) ~ φ1(x0))
对于每处X的截面,都有 S = ∫ f(x,y) dy,积分区间(φ2(x0) ~ φ1(x0))
到此,只解决了一个底面的问题。
2. 假如从a开始,每一个△X,计算一次面积,加起来就是体积,也就是:
V = Σ S △X , 当三角形X被切成无穷小,则有:
V = ∫ S dx ,积分区间(a ,b)
所以,求V分两步走:
1. 求S,将f(x, y) 中的x当做常数,在区间(φ2(x) ~ φ1(x))求积分, 即求出F(φ2(x)) - F(φ1(x)) 。 F即关于y的原函数。
2. V = ∫ S dx 应该只剩x了,按老办法,对S在区间(a ,b)积分。