题意
给你(n)种颜色,让你给一个rhombic hexecontahedron的每一个面染色,要求第(i)种颜色使用不少于(a_i)次,求有多少本质不同的rhombic hexecontahedron。定义本质不同为存在一种旋转方案使得旋转前和旋转后不一样。
答案对任意数(m)取模。
rhombic hexecontahedron是什么呢?

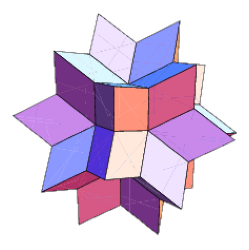
real!
题解
pólya练手题然而并不会。我真是个白学家。
这个rhombic hexecontahedron本质上是从正十二面体进行一些操作变过来的。
正十二面体长这样

容易想到rhombic hexecontahedron的每个面都可以和正十二面体的每个顶点与做一个映射。这不是双射,因为正十二面体的每个顶点被三个面共用,所以要把一个点拆成三个,才能建立双射。
但是实际上并不需要在十二面体上考虑,只是帮助我们思考旋转的问题。
考虑有多少种不同的旋转作用在这个对象集合上:
1.以两个相对面的中心连线为轴,可以旋转(frac {2pi}{5}),(frac {4pi}{5}),(frac {6pi}{5}),(frac {8pi}{5});
2.以两个相对棱的中点连线为轴,可以旋转(pi);
3.以两个相对顶点连线为轴,可以旋转(frac {2pi}{3}),(frac {4pi}{3});
4.不旋转。
任何一种旋转都是这里的一个,所以我们可以确定,整个旋转群里的置换就这么多。
1.(12 / 2 * 4 = 24);
2.(30 / 2 * 1 = 15);
3.(20 / 2 * 2 = 20);
4.(1)。
总共(24 + 15 + 20 + 1 = 60)个置换。
然后套用pólya。
考虑对于共轭的置换一起算,一共有4个共轭类,分别计算即可。
考虑然后计算一个共轭类的答案,以第一种置换为例。
由于这个共轭类内所有置换的所有轮换的长度都是一样的,(len = 5),由于对象数量为(60)(即rhombic hexecontahedron的菱形面数),所以共有(12)个轮换。
考虑设计dp,(f_{i, j})表示用前(i)种颜色,对前(j)个轮换染色的方案数。
转移方程即为:
其中(upper)就是轮换个数,(lower)则是颜色(i)至少用了(a_i)次需要的最少轮换数(在这个共轭类中)。这个可以(O(1))计算。
最后,这个共轭类的答案就是(f_{n, 12} * 24),其中12是轮换个数,24是共轭类大小。
复杂度(O(n 60 ^ 3))。
有一个要注意的地方,因为最后答案还要除掉群的大小,大小是60,可能没有逆元。所以我们一开始把模数设为(m * 60),中间都对这个东西取模(还要要用慢速乘),最后再把(60)除掉。可以用反证来证明这样做的正确性。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 60, G = 4, len[G + 1] = {0, 1, 2, 3, 5}, siz[G + 1] = {0, 1, 15, 20, 24};
int n, m, L; ll mo, tmp, ans;
ll a[N + 1], s[G + 1], C[N + 1][N + 1], f[N + 1][N + 1];
inline int read () {
static int x;
scanf("%d", &x);
return x;
}
inline ll slow_mul (ll a, ll b) {
a %= mo, b %= mo;
ll ret = a * b - (ll)((long double)a * b / mo) * mo;
if ((ret %= mo) < 0) ret += mo;
return ret;
}
void prep () {
C[0][0] = 1;
for (int i = 1; i <= N; ++i) {
C[i][0] = C[i][i] = 1;
for (int j = 1; j < i; ++j)
C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mo;
}
}
int main () {
for (int _ = read(); _; --_) {
n = read(), m = read(), L = 60, ans = 0, mo = (ll)m * N, prep();
for (int i = 1; i <= n; ++i) a[i] = read();
if (m == 1) {puts("0"); continue;}
for (int c = 1, upp, low; c <= G; ++c) {
upp = L / len[c];
memset(f, 0, sizeof f), f[0][0] = 1;
for (int i = 1; i <= n; ++i) {
low = a[i] ? (a[i] - 1) / len[c] + 1 : 0;
for (int j = low; j <= upp; ++j)
for (int k = low; k <= j; ++k)
f[i][j] = (f[i][j] + slow_mul(f[i - 1][j - k], C[j][k])) % mo;
}
ans = (ans + slow_mul(f[n][upp], siz[c])) % mo;
}
printf("%lld
", ans / N);
}
return 0;
}