先挂一个(link)
1、前置技能
(In fact),矩阵树跟树……严格意义上讲，并没有什么很大的关系，因为这个定理是基于图的，而不是基于树的。而对于这个定理，我们需要一系列前置操作：
一、对于矩阵的一堆定义：
(G)是一张无向图:
(D_{I,j})表示为度数矩阵，其中(D_{i,i})记录第(I)个节点的度数。
(A_{I,j})表示为邻接矩阵，其中(A_{i,j})记录这两点之间连了多少条边。
(K_{I,j})称为“基尔霍夫矩阵”((color{cyan}{Kirchhoff})),而基尔霍夫矩阵的定义式为：$$mathcal{K = D - A}$$
以上矩阵显然都会是(N imes N)的qwq。
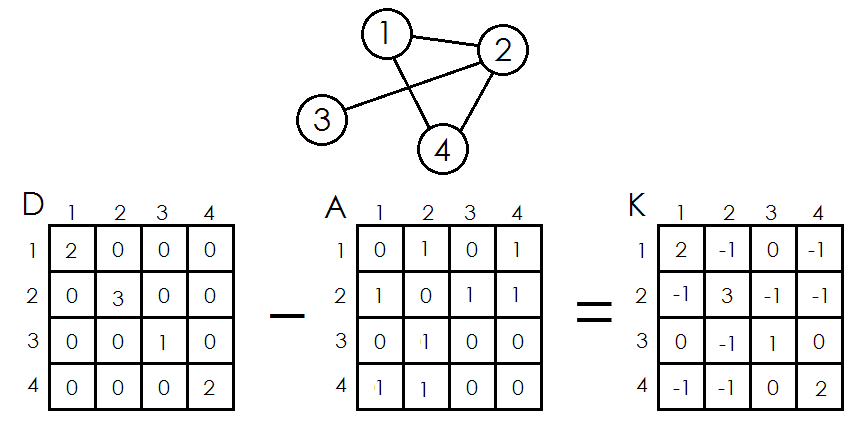下图是从网上扒翻出来的例子QAQ
二、对于行列式的一堆知识：
对于(N)阶行列式(det(A))的“主子式”,可以理解为是$A_{i,i} i in [1,n] $的余子式。
而对于一个行列式，我们要求它的值，可以根据其定义(N!)算出，用到的式子是这个：
$$sumlimits_{}{}{(-1)kprodlimits_{1}^{n}{a_{i,b_i}}} = det(A) $$,
其中(b_1)$b_n$是$1$(n)的一种排列。
显然的是，这个算法是(O(N!))的，所我们并不能这么做。那我们可以根据其性质展开类似高斯消元一样的算法，使其成为倒三角，然后对角线相乘(over).
int I, j, k, ans ;
int Gauss_work()
{
ans = 1;
for(i = 1; i < n; i ++)
{
for(j = i + 1; j < n; j ++)
while(f[j][i]){
t = f[i][i] / f[j][i];
for(k = i; k < n; k ++)
f[i][k] = (f[i][k] - t * f[j][k] + mod) % mod;
swap(f[i], f[j]);
ans = - ans;
}
ans = (ans * f[i][i]) % mod;
}
return (ans + mod) % mod;
}
还是老套路，(i)枚举主对角线上的第几个第几个元素，(j)枚举剩下的行，然后和每一行辗转相除(qwq)，在这时(k)的枚举用来按位加减。
这个玄学的代码，为了防止出现double，所以采取辗转相除的方式，具体的辗转相除是这一段代码
while(f[j][i]){
t = f[i][i] / f[j][i] ;
for(k = i; k < n; k ++){
f[i[k] = f[i][k] - t * f[j][k] ;
}
swap(f[j], f[i]) ;
ans = -ans ;
}
这样既保证了会消成(0)，又可以不出(double)，而我们需要注意在最后，(ans = -ans)，因为对换一行或者一列使得其值取反(qwq)。
2、那么矩阵树该登场啦！
根据基尔霍夫矩阵，我们随意取它的任意一个(n - 1)阶主子式（可证明对于任意的(i)是等价的），然后求出主子式的值，得到的就是在这个图中生成树的数量
然而证明……我并不会证明……我怎么这么弱啊……
放心吧，等到今年暑假结束之前，我一定要回来完善这篇博客的！
扩展定理：
也叫做“变元矩阵树定理”，如果我们把邻接矩阵变成边权矩阵，即(A_{i,j})表示(i,j)两条边之间的边权，(D_{i,i})表示与第(i)个节点的相连的边的边权和，那么我们可以得到基尔霍夫矩阵就是所有生成树中的边权之积的和
也就是$$mathcal{K = D - A } $$ $$mathcal{det(K) = sumlimits_{T}^{}{prodlimits_{I = 1}^{n-1}{w_i}}}$$
先把朴素矩阵树定理的(code)撂这儿吧
#include <cstdio>
#include <cstring>
#include <iostream>
#define il inline
#define MAXN 2225
#define ll long long
using namespace std ;
ll N, T, M, ans = 1;
ll K[MAXN][MAXN] ;
ll a, b, i, j, k, t ;
il ll gauss_work(){
for( i = 1; i < N ; i ++){
for(j = i + 1; j < N ; j ++){
while(K[j][i]){
t = K[i][i] / K[j][i] ;
for(k = i; k < N; k ++)
K[i][k] = K[i][k] - t * K[j][k] ;
swap(K[i], K[j]) ;
ans = -ans ;
}
}
ans *= K[i][i] ;
}
return ans ;
}
int main(){
cin >> T ;
while(T --){
ans = 1 ;
scanf("%d%d", &N, &M) ;
memset(K, 0, sizeof(K)) ;
for(i = 1; i <= M; i ++){
scanf("%d%d", &a, &b) ;
K[a][a] ++ ;
K[b][b] ++ ;
K[a][b] -- ;
K[b][a] -- ;
}
printf("%d
", gauss_work()) ;
}
}
然后高消的，在spoj上过了上一份代码在SPOJ上WA了…但没有大问题，应该是编译器的锅
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std ;
const int MAXN = 3010 ;
const double eps = 1e-12 ;
int N, T, M, a, b, i, j, k, t ; double K[MAXN][MAXN] ;
int _back(int x) {if(x <= eps || x >= -eps ) return 0 ;else return x < 0 ? -1 : 1 ;}
void Gauss_work(){
N -- ; int big ; double t, ans = 1 ;
for(i = 1; i <= N; i ++){
big = i ;
for(j = i + 1 ; j <= N; j ++)
if(_back(K[big][i] - K[j][i]) < 0 ) big = j ;
if(big != i) swap(K[i], K[big]) ; if(!K[i][i]) {printf("0
") ; return ;}
for(j = i + 1; j <= N; j ++){
t = K[j][i] / K[i][i] ;
for(k = i; k <= N + 1; k ++)
K[j][k] -= t * K[i][k] ;
}
}
for(i = 1; i <= N; i ++) ans = ans * K[i][i];
printf("%.0f
",abs(ans)) ;
}
int main(){
cin >> T ;
while(T --){
scanf("%d%d", &N, &M) ;
memset(K, 0, sizeof(K)) ;
for(i = 1; i <= M; i ++){
scanf("%d%d", &a, &b) ;
K[a][a] ++ ;
K[b][b] ++ ;
K[a][b] -- ;
K[b][a] -- ;
}
Gauss_work() ;
}
return 0 ;
}