引言
树作为一种特殊的图,具有很多良好的性质,树的直径便是其中之一。
定义
树的直径有许多相近的定义。但由于没有找到比较权威的定义,就用自己的语言大概表述一下吧。
对于一棵带非负边权的树,定义两点间距离为两点间路径的边权之和,树的直径就是距离最远的两点之间的路径,同时也称该距离为树的直径。
简而言之,树的直径就是树上最长的简单路径。
性质
-
直径两端点一定是两个叶子节点。
-
距离任意点最远的点一定是直径的一个端点。
-
对于两棵树,如果第一棵树直径两端点为(u,v),第二棵树直径两端点为(x,y),用一条边将两棵树连接,那么新树的直径一定是u,v,x,y中的两个点。
性质证明
-
显然成立,证明从略。
-
情况一:点a在直径((u,v))上。若存在点b使得$ dis(a,b) gt dis (a,u) ext{并且} dis(a,b) gt dis (a,v)$ ,则有 (dis(b,v) ext{或} dis(b,u) gt dis(u,v)),即((u,v))不是该树的直径,矛盾。
情况二:点a不在直径((u,v))上。若存在点b使得$ dis(a,b) gt dis (a,u) ext{并且} dis(a,b) gt dis (a,v)$ ,不妨取直径的其中一个端点(u)分析。
分析图如下(灵魂画手上线):
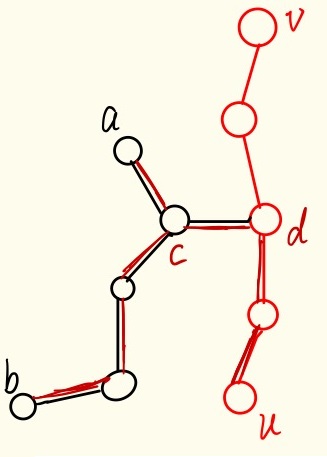
图片注:(u),(v) 为直径端点,(c)为((a,b) ext{与}(a,u))交点,(d)为((a,u) ext{与}(v,u))交点。
由于(dis(a,b) gt dis (a,u)) ,可知 (dis(c,b) gt dis (c,u)),进而得到(dis(d,b) gt dis (d,u)),最终可知(dis(v,b) gt dis (v,u)),即((u,v))不是该树的直径,矛盾。
-
如果新树直径不是原来两棵树中一棵的直径,那么新直径一定经过两棵树的连接边,新直径在原来每棵树中的部分一定是距离连接点最远的点,即一定是原树直径的一个端点。
求解算法
共有两种时间复杂度为 (O(N)) 的算法,一种是dp,另一种是贪心算法。
方法一:动态规划
根据定义,我们只需要求出最大链长即可。
首先将该树转化为有根树。设(f[i])为以节点(i)为根的子树的最大深度,有状态转移方程$$f[i] = max_{j in s(i)}f[j]+1 quad ext{where (s(i)) is the set of the son nodes of node i.}$$那么在该子树中经过节点(i)的最长链长度为 (f[i]) 与次大 (f[j]) (缺省值为0)之和。在整个遍历过程中记录最大链长即可。
方法二:贪心算法
根据树的直径性质2,我们只需要任取一点(s)开始DFS(或BFS)即可找到距离该点的最远点,即直径端点之一,记为(u)。同样的,从节点(u)开始我们便可以找到另一个端点(v),过程中记录距离即可得到树的直径。
相较于方法一,方法二可以更方便地找到直径的端点,进而得到直径的具体路径。
Code
暂略