- SGD
- Momentum
- RMSprop
- Adam

SGD
(g_t= abla_{ heta_{t-1}}{f( heta_{t-1})})
(Delta{ heta_t}=-eta*g_t)
其中,(eta)是学习率,(g_t)是梯度 SGD完全依赖于当前batch的梯度,所以(eta)可理解为允许当前batch的梯度多大程度影响参数更新
缺点
- 选择合适的learning rate比较困难
- 对所有的参数更新使用同样的learning rate。对于稀疏数据或者特征,有时我们可能想更新快一些对于不经常出现的特征,对于常出现的特征更新慢一些,这时候SGD就不太能满足要求了
SGD容易收敛到局部最优,并且在某些情况下可能被困在鞍点
Momentum

十分曲折,走了不少弯路,在纵向我们希望走得慢一点,横向则希望走得快一点,所以才有了动量梯度下降算法。
momentum是模拟物理里动量的概念,积累之前的动量来替代真正的梯度。公式如下:
(m_t=mu*m_{t-1}+g_t)
(Delta{ heta_t}=-eta*m_t)
其中,(mu)是动量因子

梯度下降速度综合之前的步骤,则各个方向上不会波动太大(平均值抵消)超参数 beta=0.9
Root Mean Square Prop
均方根传播
dW变成dW的平方,在下降的时候多除以了一个根号项。
使用指数加权平均计算均方差,然后W,b更新时候除自己方向上的均方差,这样均方差小的,即波动小的步子大。反之步子小。这样就可以消除下降中的摆动,可以采用较大的学习率快速学习。为了确保除以的分母不会为0,在实操上会加上一个很小的数ε。
指数加权平均 (V_t=V_t-1 * alpha + (1-alpha) * heta)
计算步骤:
(S_{dw}=βS_{dw}+(1-β)dw^2)
(S_{db}=βS_{db}+(1-β)db^2)
(w:=w-αfrac{dw}{sqrt{S_{dw}}})
(b:=b-αfrac{db}{sqrt{S_{db}}})
Adam
Momentum是为了对冲mini-batch带来的抖动。
RMSprop是为了对hyper-parameter进行归一。
这两个加起来就是Adam了。

学习率衰减
之前算法中提到的学习率α都是一个常数,这样有可能会一个问题,就是刚开始收敛速度刚刚好,可是在后面收敛过程中学习率偏大,导致不能完全收敛,而是在最低点来回波动
decay_rate:衰减率
epoch_num: 迭代次数
公式:(α=frac{1}{1+decay_rate*epoch_num}α_0)
局部最优
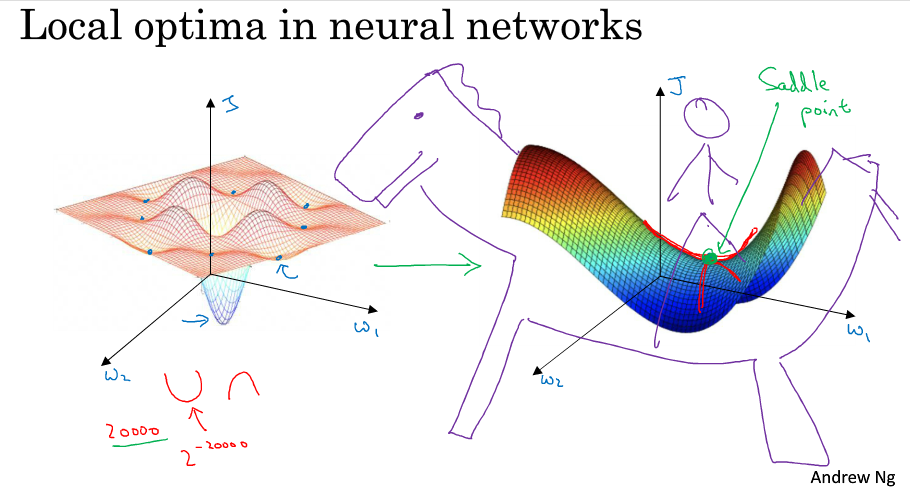
早期,人们总担心一个优化问题可能会出现多个局部最优点,认为很有可能算法陷入局部最优而无法做出正确的求解。
通常梯度为0的点不会是下图左侧的那些局部最优点,而是下图右侧的这个鞍点。鞍点可以理解为在某一方向上是极大值点,在另一方向上是极小值点,可以想象成马背上的马鞍
所以在深度学习中(假设你有大量参数,代价函数被定义在高维空间)你不太可能陷入局部极值点,但是位于鞍点这样的平稳地段你可能学习的非常慢,所以才有了momentum,RMSProp,adam这样的算法来加快运算。