树状数组从入门到入土

我们为什么使用树状数组？

 （参考了 http://hzwer.com/914.html）

如果给定一个数组，要你求里面所有数的和，一般都会想到累加。但是当那个数组很大的时候，累加就显得太耗时了，时间复杂度为O(n)，并且采用累加的方法还有一个局限，那就是，当修改掉数组中的元素后，仍然要你求数组中某段元素的和，就显得麻烦了。所以我们就要用到树状数组，他的时间复杂度为O（lgn），相比之下就快得多。下面就讲一下什么是树状数组：

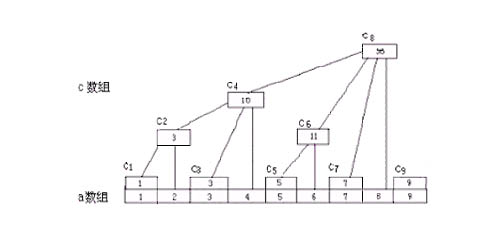
下面来分析一下上面那个图看能得出什么规律：

据图可知：c1=a1，c2=a1+a2，c3=a3，c4=a1+a2+a3+a4，c5=a5，c6=a5+a6，c7=a7，c8=a1+a2+a3+a4+a5+a6+a7+a8，c9=a9，c10=a9+a10，c11=a11……..c16=a1+a2+a3+a4+a5+…….+a16。

分析上面的几组式子可知：

• 当 i 为奇数时，ci=ai ；
• 当 i 为偶数时，就要看 i 的因子中最多有二的多少次幂，例如，6 的因子中有 2 的一次幂，等于 2 ，所以 c6=a5+a6（由六向前数两个数的和），4 的因子中有 2 的两次幂，等于 4 ，所以 c4=a1+a2+a3+a4（由四向前数四个数的和）。

（一）有公式：c_n=a_(n-2^k+1)+………+a_n（其中 k 为 n 的二进制表示中从右往左数的 0 的个数）。

cn包含了从an向前数n-2^k+1的a（即n的因子中的二次幂的a）

那么，如何求 2^k 呢？求法如下：

int lowbit(int x)
{
     return x&(-x);    
}

lowbit（）的返回值就是 2^k 次方的值。

求出来 2^k 之后，数组 c 的值就都出来了；

接下来我们要求数组中元素的和。

（二）当我们求（1, r）的区间和时，在上图看作是从c_r对应的格子出发,不断向左上方移动的过程；统计遇到的每个格子，就能最终求出整个区间的和。（通过前面对cn规律的观察也不难证明）

实现我们利用的还是二进制，即将下标（r）按二进制拆分成几段来统计；

算法流程如下：

（1）首先，令sum=0，转向第二步；

（2）接下来判断，如果 n>0 的话（也就是左上角的红色格子没统计完，也即ci没有加完），就令sum=sum+c_i转向第三步，否则的话，终止算法，返回 sum 的值；

（3）n=n – lowbit（n）（将n的二进制表示的最后一个零删掉），回第二步。

代码实现：

 

 

 

 

 

 

C++

 

int Sum(int n)
{
    int sum=0;
    while(n>0)
    {
         sum+=c[n];
         n=n-lowbit(n);
    }  
    return sum;
}

（三）当数组中的元素有变更时，树状数组就发挥它的优势了，算法如下（修改为给某个节点 i 加上 x /单点修改）：

（1）当 i<=n 时，执行下一步；否则的话，算法结束;

（2）ci=ci+x ，i=i+lowbit（i）（在 i 的二进制表示的最后加零，即不断更新红色格子（ci）），返回第一步。

代码实现：

 

 

 

 

 

 

C++

void update(int i,int x)
{
     while(i<=n){
          c[i]=c[i]+x;
          i=i+lowbit(i);
     }
}

 

（树状数组的基础理论和实现就到此完满结束了）（撒花~❀） 

 

我们可以用树状数组解决什么问题？

基础问题：

• 单点修改，区间询问： https://www.luogu.org/problem/P3374
• 区间修改，单点询问： https://www.luogu.org/problem/P3368

树状数组和差分是好基友，   作为强大的区间数据结构，树状数组常常和差分一起解决问题；

--------------------------------------------------未完待续------------------------------------------------------------