矩阵分析线性系统1 定义、方程组解的表现形式和性质

1. 定义

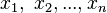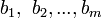线性系统（线性方程组）的一般形式如下，其中 $x_1,\ x_2,...,x_n$ 是未知数, $a_{11},\ a_{12},...,\ a_{mn}$ 是系数, $b_1,\ b_2,...,b_m$ 是常量。

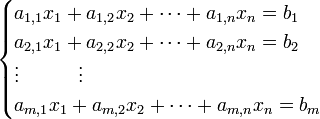
$\begin{cases}a_{1,1}x_{1} + a_{1,2}x_{2} + \cdots + a_{1,n}x_{n}= b_{1} \\ a_{2,1}x_{1} + a_{2,2}x_{2} + \cdots + a_{2,n}x_{n}= b_{2} \\ \vdots \quad \quad \quad \vdots \\ a_{m,1}x_{1} + a_{m,2}x_{2} + \cdots + a_{m,n}x_{n}= b_{m} \end{cases}$

线性方程组的列向量形式如下。从这个角落来看，常量b是系数列向量{a1,a2…,an}基于未知数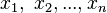 $x_1,\ x_2,...,x_n$ 的加权线性组合（linear combination）。这让我们能够利用向量空间（vector spaces）理论来分析问题。例如，系数列向量{a1,a2…,an}所有线性组合的集合称为它们张成的空间。如果在这个空间上仅有唯一的线性组合，那么这个方程有唯一解。

$x_1 \begin{bmatrix}a_{11}\\a_{21}\\ \vdots \\a_{m1}\end{bmatrix} + x_2 \begin{bmatrix}a_{12}\\a_{22}\\ \vdots \\a_{m2}\end{bmatrix} + \cdots + x_n \begin{bmatrix}a_{1n}\\a_{2n}\\ \vdots \\a_{mn}\end{bmatrix} = \begin{bmatrix}b_1\\b_2\\ \vdots \\b_m\end{bmatrix}$

线性方程组的矩阵形式 $A\bold{x}=\bold{b}$ 。The number of vectors in a basis for the span is now expressed as the rank of the matrix.

$A= \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix},\quad \bold{x}= \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix},\quad \bold{b}= \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix}$

2. 方程组的解

2.1 几何解释

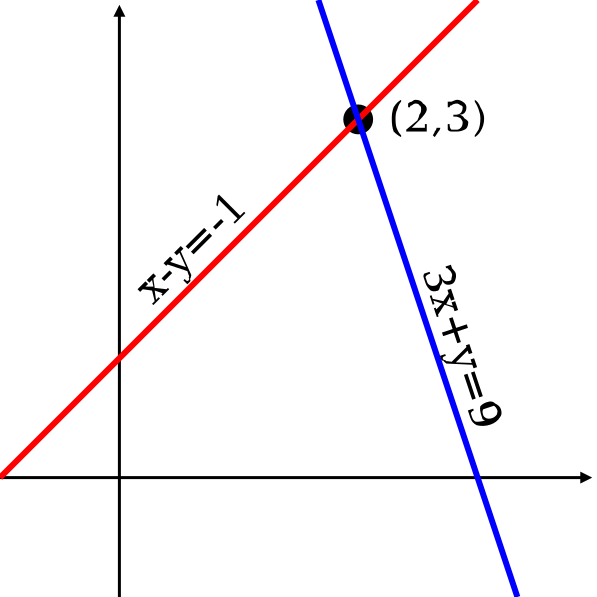
对于两个变量（x 和 y) 的系统，每个线性等式对应xy-平面上的一条线，线上的点满足此线性公式。对于这个线性系统（线性方程组），它的解必须满足所有线性公式，因此它的解是所有线的交集，从而有三种情况：1）交集是一个点，有唯一解；2）是一条直线，有无穷个解；3）是空集，不存在解。

当有3各变量时，每个线性方程对于一个三维空间上的面。当有n各变量时，每个线性方程对于一个n维空间上的超平面。

图.2变量-2线性公式-唯一解图。3变量-2线性公式-无穷解

2.2 解的表现形式

线性方程组的表现取决于方程组个数和未知数个数：

1）通常，方程个数m<未知数个数n时，有无穷多解，在某些情况下有唯一洗漱解（感知压缩，Compressed Sensing)。这样的系统称为欠定系统（underdetermined system）

2）通常，方程个数m=未知数个数n时，有唯一解。这样的系统称为恰定系统。

3）通常，方程个数m>未知数个数n时，没有解。这样的系统称为超定系统（overdetermined system）。

3. 方程组的性质

3.1 独立性（Independence）

当线性方程组任一个方程都不能从其他方程推导出来时，称线性系统的方程是独立的。此时，每个方程含有变量的新信息。线性方程的独立性等价于线性独立（linear independence）。

例如，下面方程组不独立，因为第3各方程是前两个方程的和，图形如下

$\begin{alignat}{5} x &&\; - \;&& 2y &&\; = \;&& -1 & \\ 3x &&\; + \;&& 5y &&\; = \;&& 8 & \\ 4x &&\; + \;&& 3y &&\; = \;&& 7 & \end{alignat}$

3.2 一致性（Consistency）

当线性方程组中方程的解相同时，称线性系统的方程是一致的。当它们不一致时，导致矛盾，如1=3。

例如，下面方程组不一致，因为它导致6=12。由图可见，这两个不一致的方程对应两个平行线。

$3x+2y=6\;\;\;\;\text{and}\;\;\;\;3x+2y=12$