对于一个字符串,请设计一个高效算法,计算其中最长回文子串的长度。
给定字符串A以及它的长度n,请返回最长回文子串的长度。
"abc1234321ab",12
返回:7
1 import java.util.*; 2 //法1:动态规划 时间复杂度O(n^2),空间复杂度O(n^2) 3 public class Palindrome { 4 public int getLongestPalindrome(String A, int n) { 5 // write code here 6 int[][] dp=new int[n][n]; 7 //dp[i][j]表示位置从i到j的元素,若为回文串则存其长度,若不为回文串则为0; 8 for(int i=0;i<n;i++){ 9 dp[i][i]=1; 10 } 11 int max=1; 12 char[]a=A.toCharArray(); 13 for(int len=2;len<=n;len++){ 14 //len表示其子串的长度,由于长度为1的子串必为回文串,所以len从2开始到其最大子串及它本身n 15 for(int i=0;i<=n-len;i++){ 16 //i表示子串的开始位置,j表示子串结束的位置 17 int j=i+len-1; 18 //下面开始比较 19 if(len==2&&a[i]==a[j]){ 20 dp[i][j]=2; 21 max=2; 22 } 23 else if(a[i]==a[j]&&dp[i+1][j-1]!=0){ 24 dp[i][j]=len; 25 max=len; 26 } 27 } 28 } 29 return max; 30 31 } 32 } 33 //*********************************************************************** 34 import java.util.*; 35 //法2:中心扩散法 时间复杂度O(n^2)空间复杂度O(n) 36 public class Palindrome { 37 int max=1; 38 public int getLongestPalindrome(String A, int n) { 39 // write code here 40 char[] a=A.toCharArray(); 41 for(int i=0;i<n;i++){ 42 //此时遍历的是子字符串的中心点 43 findPalindrome(a,i,0); 44 //当最长回文子串长度为奇数时,则中间的数只有一个,用此可找出最长回文子串 45 findPalindrome(a,i,1); 46 //当最长回文子串长度为偶数时,则位于中间的数有2个,用此可找出最长回文子串 47 } 48 return max; 49 } 50 private void findPalindrome(char[] a,int index,int offset){ 51 52 int left=index; 53 int right=index+offset; 54 while(left>=0&&right<a.length&&a[left]==a[right]){ 55 //利用双指针记录位置,从中心往外扩散,只要是回文串,则指针一直往外移 56 left--; 57 right++; 58 } 59 //当循环结束时,left和right的上一个坐标对应的便是此次中心点的最长回文串开始和结束的位置 60 int len=right-left-1; 61 //max=(right-1)-(left+1)+1 62 if(len>max) max=len; 63 //将此次的长度与全局长度比较,若此次较大则更新全局长度 64 } 65 } 66 /*相对于动态规划,从子串长度为2开始遍历,一直到子串长度为n,对于每一个新子串, 67 只要他的两边元素相等且他里面也是回文串则该子串便是回文串,我们通过一个表dp[i][j] 68 来保存每个子串是否为回文串的信息,但是这些信息并不是一直都会用到,长为4的串只 69 会用到长为2的串的信息,长为6的串只会用到长为4的串的信息,而此时长为2的串的信息 70 已经用不到了,所以我们便可以用中心扩散法来保存每次需要的信息即可,让一个中心点 71 从串的开头走到结尾,只要每次满足中心点(即指针)两边元素相等且指针范围在串的长 72 度范围内,便不断向外发散,每次都保存当前最长串的长度,则遍历结束时必然得到最长 73 回文串的长度 74 */
此题还有着时间复杂度为O(n),空间复杂度为O(n)的马拉车算法,先存下,等我开始研究字符串常见算法时,再来实现
又遇到了同类型的题,思路是一模一样的
题目如下:longest-palindromic-substring
Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.
这次是找出最长的回文串
法1:使用中心扩散法
1 public class Solution { 2 int left=0; 3 int max=1; 4 public String longestPalindrome(String s) { 5 char[] cs=s.toCharArray(); 6 for(int i=0;i<cs.length;i++){ 7 findPailndromic(cs,i,i); 8 findPailndromic(cs,i,i+1); 9 } 10 return s.substring(left,left+max); 11 } 12 public void findPailndromic(char[]cs,int i,int j){ 13 while(i>=0&&j<cs.length&&cs[i]==cs[j]){ 14 if(max<j-i+1){ 15 left=i; 16 max=j-i+1; 17 } 18 i--; 19 j++; 20 } 21 } 22 }
法2:使用马拉车算法
1 //时间复杂度(n) 2 public class Solution { 3 public String longestPalindrome(String s) { 4 5 int[] p; 6 StringBuilder sb = new StringBuilder(); 7 //对字符串进行预处理 8 sb.append('$'); 9 sb.append('#'); 10 for(int i=0;i<s.length();i++){ 11 sb.append(s.charAt(i)); 12 sb.append('#'); 13 } 14 int mx=0; 15 int ans=0; 16 int id=0; 17 p=new int[sb.length()]; 18 for(int i=1;i<sb.length();i++){ 19 20 if(mx>i){ 21 p[i]=Math.min(p[2*id-i], mx-i); 22 }else 23 p[i]=1; 24 while(i+p[i]<sb.length()&&i-p[i]>=0&&sb.charAt(i-p[i])==sb.charAt(i+p[i])){ 25 p[i]++; 26 } 27 28 if(p[i]+i>mx){ 29 id=i; 30 mx=p[i]+i; 31 } 32 ans = Math.max(ans, p[i]); 33 } 34 int max=0; 35 int k=0; 36 for(int i=0;i<p.length;i++){ 37 38 if(p[i]>max){ 39 k=i; 40 max=p[i]; 41 } 42 } 43 StringBuilder sb1= new StringBuilder(); 44 for(int i=k-max+1;i<k+max-1;i++){ 45 46 if(sb.charAt(i)!='#'&&sb.charAt(i)!='$'){ 47 sb1.append(sb.charAt(i)); 48 } 49 } 50 return sb1.toString(); 51 } 52 }
下面讲解一下我对马拉车算法的理解:
例如给定一个字符串s=" noon"
如果首先采用中心扩散法求解时,我们需要做的事情依次为:
从第0个字符 ' n'开始向两边扩展,该字符串有偶数个,设最大回文长度为max=1
所以首先判断s[0]是否与s[1]一样,发现不符,此时以该字符为中心的最大回文串长度便为1,更新全局最大的回文长度max,进入下一次循环
判断s[1]y与s[2]是否一样,发现一样,继续判断s[0]与s[3]是否一样,发现一样,继续向两边移动直至超出了边界条件,此时以该字符为中心的最大回文串长度便为2,将此时局部最长的与全局最长的进行比较,更新全局最大的回文长度max=2;
然后我们将中心字符继续往后移动,继续计算当中心字符为s[2]时对应的最大回文串,当中心字符为s[3]时对应的最大回文串
一整趟循环下来,我们会得到全局最长的回文串的长度max
而对于马拉车算法,为什么它要快于中心扩散法,因为其还多做了以下两点
1.首先对于字符串进行预处理,使其不必要进行奇偶的判断
而处理方法很好理解,对于一个长为n的字符串,我再加入n个分割符,此时总长度为2n,必然为偶数,同理,若加入n+1个分隔符,则必然为奇数
2.在找到全局最长的回文子串之前,马拉车算法原理与中心扩散法原理是基本一样的,都是以一个字符为中心向两边扩散,然后记录符合要求的最长子串的信息;
而在找到全局最长的回文子串之后,此时马拉车算法就不再进行计算了,而是直接进行查表,得出所要的信息(感觉此处有点动态规划的味道,只不过并没有显式地把信息存下来)
那么,问题来了,为什么我可以在全局最长的回文串内可以直接查表得到所需信息呢?
这就是马拉车算法的原理
我们以noon这个字符串为例子,进行一下讲解
首先,对于这个字符串进行预处理:
StringBuilder sb = new StringBuilder(); 7 //对字符串进行预处理 8 sb.append('$'); 9 sb.append('#'); 10 for(int i=0;i<s.length();i++){ 11 sb.append(s.charAt(i)); 12 sb.append('#'); 13 }
得到
0 1 2 3 4 5 6 7 8 9
$ # n # o # o # n #
我们使用一个数组p[] 来保存以每个字符p[i]为中心,所能得到的对应最长回文子串的半径,
如对于一个字符串$#n ,当中心字符为#时,它此时所对应的回文子串就是它本身,p[1]=1;
如对于一个字符串 #n#,当中心字符为n时,它所对应的回文子串就是#n#,p[1]=2;
故p[i]就表示以字符串s[i]为中心的最长回文字串的最端右字符到s[i]的长度。
对于上面这个简单的例子,我们可以得到其p数组为
| 序号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 字符串 | $ | # | n | # | o | # | o | # | n | # |
| p[]数组 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 |
如果我们已经知道了p[i]数组,
对于数组p[],有一性质,p[ i ]-1就是该回文子串在原字符串S中的长度 ,那就是p[i]-1就是该回文子串在原字符串S中的长度,至于证明,首先在转换得到的字符串T中,所有的回文字串的长度都为奇数,那么对于以T[i]为中心的最长回文字串,其长度就为2*P[i]-1,经过观察可知,T中所有的回文子串,其中分隔符的数量一定比其他字符的数量多1,也就是有P[i]个分隔符,剩下P[i]-1个字符来自原字符串,所以该回文串在原字符串中的长度就为P[i]-1
另外,由于第一个和最后一个字符都是#号,且也需要搜索回文,为了防止越界,我们还需要在首尾再加上非#号字符,实际操作时我们只需给开头加上个非#号字符,结尾不用加的原因是字符串的结尾标识为'�',等于默认加过了
所以,现在的问题是如何去求出数组p[]
我们继续以上面那个例子来讲
首先
设全局最长的回文串的中心位置为id ( 在上面的例子中对应着p[5],即id=i=5)
mx 代表以p[id]为中心的最长回文最右边界,也就是mx=p[id]+id; (mx对应着上面例子的mx=5+5,即mx=10,mx表示的是最右边界,也就是不能超过或等于它)
整个算法的核心在于这句:
p[i] = i<mx? min(p[2 * id - i], mx - i) : 1;
这句话是用来求p[i]数组初值
可以看出 当i<mx时,也就是当此时的字符在最长回文字符内部时
p[i]=min(p[2*id-i],mx-i);
当i>=mx时,也就是此时的字符在最长回文字符的外面时
p[i]=1;
当 mx - i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 P[i] = P[j],见下图。
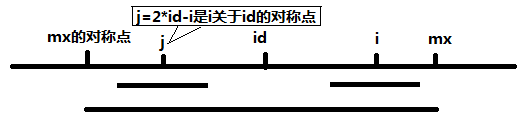
当 P[j] >= mx - i 的时候,以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中,但是基于对称性可知,下图中两个绿框所包围的部分是相同的,也就是说以S[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx - i。至于mx之后的部分是否对称,就只能老老实实去匹配了。
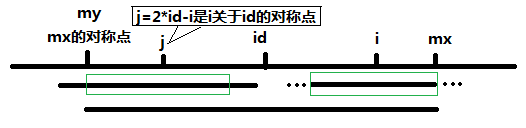
对于 i >=mx 的情况,无法对 P[i]做更多的假设,只能P[i] = 1,然后再去匹配了。
以上这两个图和话直接来自网上,当我看懂马拉车算法后,我觉得这段话讲的很详细,可是,当我在第一次看马拉车算法的时候,我就搞不懂为什么他要这么写,加来加去的还要求最小值
为什么要这样搞?直接看这些结论是不好搞懂的,让我们深入程序执行的整个过程,搞清楚算法做了什么,就比较好明白为什么此处这样写
我们继续以上面那个例子来讲解
整个求p[i]数组的代码如下:
1 int mx = 0, id = 0, resLen = 0, resCenter = 0; 2 for (int i = 1; i < t.size(); ++i) { 3 p[i] =i< mx ? min(p[2 * id - i], mx - i) : 1; 4 while (t[i + p[i]] == t[i - p[i]]) ++p[i]; 5 if (mx < i + p[i]) { 6 mx = i + p[i]; 7 id = i; 8 } 9 if (resLen < p[i]) { 10 resLen = p[i]; 11 resCenter = i; 12 } 13 }
所要求的字符串如下:
| 序号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 字符串t | $ | # | n | # | o | # | o | # | n | # |
首先,我们让全局最长回文串的中心位置id为0,让全局最长回文串的边界mx为0
resLen表示当下此时的回文串的长度,初值也为0,resCenter表示当下此时的回文串的中心位置,初值也为0,
当i=1时,i>mx,即此时字符是t[i]在最长回文子串的外面,是t[1]的回文子串为他自己本身,所以p[1]=1 while (t[i + p[i]] == t[i - p[i]]) ++p[i];,这句话与中心扩散法的原理一样,就是向两边扩散找,对于此例,t[0] != t[2],未进入循环,故p[1]=1不变 此时开始更新全局最长回文串的id 与 mx 由mx < i + p[i] 所以此时mx=i+p[i]=2 ,id=1 此时开始更新当下此时的回文串的 resLen,resCenter 由resLen < p[i] 所以此时 resLen=p[i]=1,resCenter=i=1; 当i=2时 i=mx,即此时字符是t[i]在最长回文子串的边界上,p[2]=1 while (t[i + p[i]] == t[i - p[i]]) ++p[i]; 向两边扩散找,对于此例,t[1] == t[3],故p[2]++,所以p[2]=2; 更新全局 由mx<i+p[i]=4 所以此时 mx=4,id=2 更新当下 由resLen < p[i]=2, 所以resLen=2, resCenter=2; 当i=3时 i<mx p[i]=min(p[2 * id - i],mx-i)
我们在上次循环所求出的全局回文串里看
0 1 2 3 4
$ # n # o
由于中心位置id=2,如果我们以i=2为对称轴,可以看出 p[3]=p[1] ,至于p[1]中的1怎么来的 由图中位的对称关系可以得到 j=id*2-i ,所以有p[i]=p[j]
但是,这只是其中一种情况,如果p[1]=3,那么当p[3]=p[1]=3时,我们发现p[3]的边界(3+p[3]=6>4)已经在当前全局边界的外面了,对于在全局回文串外面的情况,需要另行判断
所以p[i]的取值是受到边界的约束的,即p[i]<=mx-i
所以 p[i]=min(p[2 * id - i],mx-i)
对于此例,p[3]=p[1]=1
while (t[i + p[i]] == t[i - p[i]]) ++p[i]; 向两边扩散找,对于此例,t[2] != t[4],,所以p[3]=1;
更新全局 由mx=i+p[i]=4 所以不变
更新当下 由resLen >p[i]=1, 所以不变
当i=4时,i=mx,所以 p[4]=1
while (t[i + p[i]] == t[i - p[i]]) ++p[i]; 向两边扩散找,对于此例,t[3] == t[5],故p[4]++,所以p[4]=2;
更新全局 由mx<i+p[i]=6 所以mx=6,id=4 更新当下 由resLen =p[i], 所以不变
当 i=5时 i<mx=6 p[i]=min(p[2 * id - i],mx-i)
我们在上次循环所求出的全局回文串里看
2 3 4 5 6
n # o # o
p[5]=p[3]=1
while (t[i + p[i]] == t[i - p[i]]) ++p[i]; 向两边扩散找,对于此例,t[4]== t[6],t[3]==t[7],t[2]==t[8],t[1]==t[9]所以p[3]=5;
更新全局 由mx<i+p[i]=10 所以mx=10,id=5 更新当下 由resLen <p[i]=5, 所以resLen=p[i]=5 , resCenter=i=5
在此处已达最长的回文串,所以全局不会再变了,而对于局部最长的回文串,由于之后碰到的p[i]必定小于此处的p[i],所以局部也不变了
当 i=6 时 i<mx 所以p[6]=min(p[4],4)=2
当i=7,8,9时,同理
最终,函数
return s.substr((resCenter - resLen+1) , resCenter+resLen-1);
然后再去掉之前添加上的'$' 与'#',便得到最长回文子串
现在,我们再返回去看开始时的那两个图,就比较好懂了
参考博客:马拉车算法