主因子分析，在炼数成金课程中提到：
降维的一种方法，是主成分分析的推广和发展
是用于分析隐藏在表面现象背后的因子作用的统计模型。试图用最少个数的不可测的
公共因子的线性函数与特殊因子之和来描述原来观测的每一分量
例子：各科学习成绩（数学能力，语言能力，运劢能力等）
例子：生活满意度（工作满意度，家庭满意度）
例子：薛毅书P522
总结就是：把多个变量，根据主观（业务经验），或客观（具体分类算法），归为几个类别，从而使变量减少，便于分析。比如，
这里，m的值表示最后只需要2个因子，就是说最后这八项指标会变成2项指标，我们可以大概预测一下，这两项指标（因子）一般是短跑能力和长跑能力，当然你可以定义最后
的因子数为3，解释为短跑能力，中长跑能力和长跑能力。
先看这么一个矩阵：
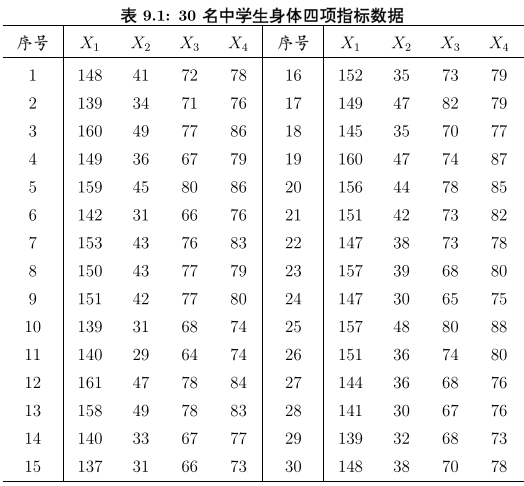
矩阵中有30个学生（样本），每个样本有4个因子，那么问题来了，比如我们希望把这4个因子分类，假设分为2类作为新的样本变量。
抽象为数学公式：
显而易见，这里有p=4，μ1是y1~y30的均值，Var（X）是X1~X4之间的协方差这里：y表示样本数（序号，同学人数），X表示每个样本的内容（测试项目）。
其实我们可以发现一个问题，我们要找的是因子之间的关系，所以只要X之间的关系，跟样本数目y（序号）没有关系，你可以这样认为：体重，身高，胸围和坐高之间肯定存在关系，身高的同学体重一般也大，但这些关系跟观察的同学人数多少没有关系，所以，我们要用的依旧是X之间的关系，即协方差！
所以，每一个观察的样本，可以描述成：
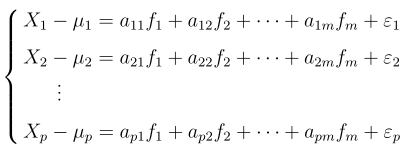
这里，我们对样本X进行了中心化，如果我们m取2，那这里就只有f1，f2两个公共新因子，ε1,ε2,···,εp为特殊因子，每个公共因子fi至少对应两个原变量X，否则就被算入特殊因子。
上述矩阵又可以简写为：
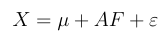
好的，我们X是直接观测得到的，Var(F)是I单位矩阵，所以我们的目的就是求A!!!
先来看三个性质：
说明：1，Σ就是X的协方差矩阵，性质1是推倒出来的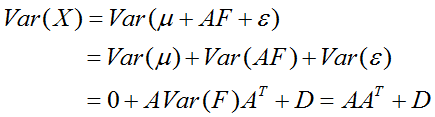
2，X矩阵同时乘以某个系数c，不影响结果。
同时引入两个指标：
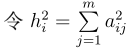
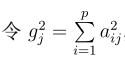
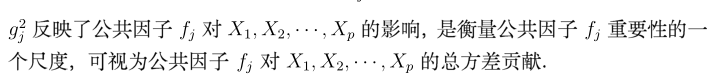
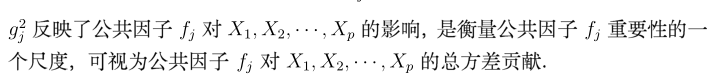
这两个指标，本人觉得没什么大用（可能只是我书读得少）。
废话少说，我们现在要根据性质1，来计算A矩阵！
在计算A矩阵前，我要先引入一个协方差分解定理。
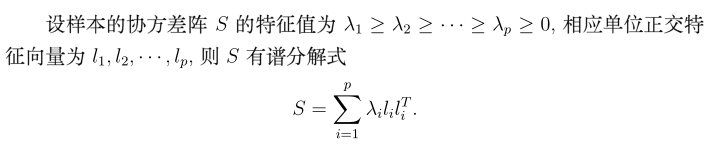
就是说S（协方差），可以拆分成多个特征值*特征向量*特征向量’的和，这里我们就可以发现主成份的影子了，不必要取到p，我们只要取前几个
贡献较大的i值即可。
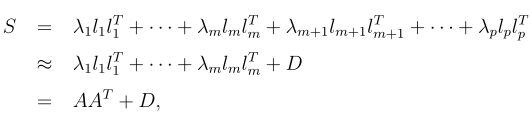
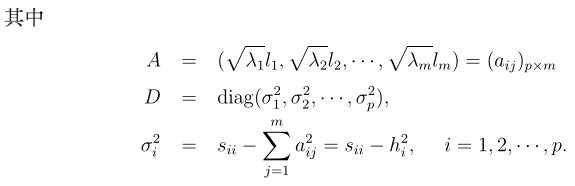
至此，可以通过以上描述求出A，但还存在一个不足
性质：矩阵旋转后，协方差不变。
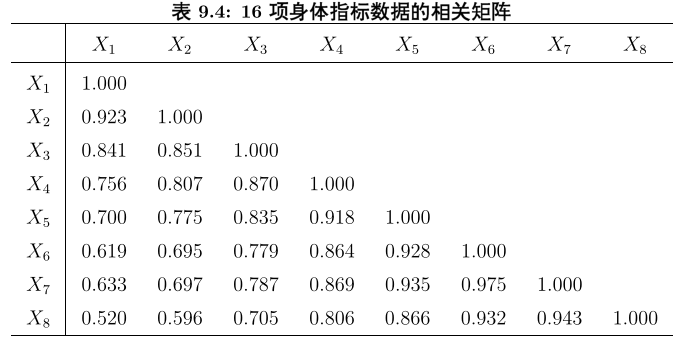
接下来，将用R语言具体分析一个事例：还以最前面的跑步数据做实验。
我们不关心具体样本，所以我们这里拿到协方差矩阵即可
//构造主成份算法的因子分析
factor.analy1<-function(S, m){ p<-nrow(S); //取行数
diag_S<-diag(S); //协方差求迹（对角线元素之和）
sum_rank<-sum(diag_S)
//取行列名 rowname<-paste("X", 1:p, sep="") colname<-paste("Factor", 1:m, sep="") A<-matrix(0, nrow=p, ncol=m, dimnames=list(rowname, colname)) eig<-eigen(S) //根据公式求A for (i in 1:m) A[,i]<-sqrt(eig$values[i])*eig$vectors[,i] //求h h<-diag(A%*%t(A)) rowname<-c("SS loadings", "Proportion Var", "Cumulative Var") B<-matrix(0, nrow=3, ncol=m, dimnames=list(rowname, colname))
for (i in 1:m){ B[1,i]<-sum(A[,i]^2) B[2,i]<-B[1,i]/sum_rank B[3,i]<-sum(B[1,1:i])/sum_rank } method<-c("Principal Component Method") list(method=method, loadings=A, var=cbind(common=h, spcific=diag_S-h), B=B) //diag_S-h求σ
}
根据具体数据：
x<-c(1.000,
0.923, 1.000,
0.841, 0.851, 1.000,
0.756, 0.807, 0.870, 1.000,
0.700, 0.775, 0.835, 0.918, 1.000,
0.619, 0.695, 0.779, 0.864, 0.928, 1.000,
0.633, 0.697, 0.787, 0.869, 0.935, 0.975, 1.000,
0.520, 0.596, 0.705, 0.806, 0.866, 0.932, 0.943, 1.000)
names<-c("X1", "X2", "X3", "X4", "X5", "X6", "X7", "X8")
R<-matrix(0, nrow=8, ncol=8, dimnames=list(names, names))
//补全x矩阵
for (i in 1:8){
for (j in 1:i){
R[i,j]<-x[(i-1)*i/2+j]; R[j,i]<-R[i,j]
}
}
source("E:/mypath/factor.analy1.R")//要写调用函数的绝对路径
fa<-factor.analy1(R, m=2); fa
E<- R-fa$loadings %*% t(fa$loadings)-diag(fa$var[,2])
sum(E^2)
结果截图：
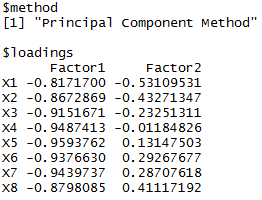
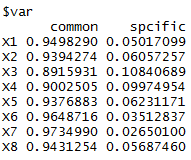
loadings中，factor1和factor2就是两个新的主因子，common=h, spcific=diag_S-h，B无关紧要，当m选择较合理时，S的实际值和估计值差距很小，即E^2很小。
最后一步，旋转因子矩阵，使因子实际意义更明显。
vm1<-varimax(fa$loadings, normalize = F); vm1 /*varimax(x, normalize = TRUE, eps = 1e-5) x载荷和矩阵，normalize是逻辑变量，表示是否进行Kaiser正则化，eps是迭代精度*/
旋转后结果：
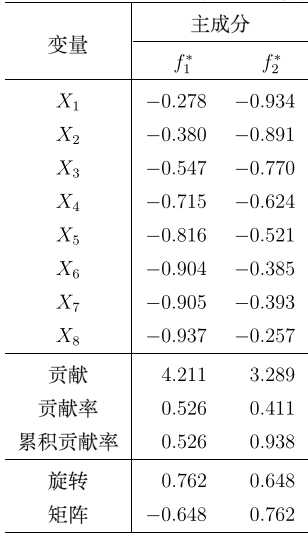可以观察明显发现，f1因子偏向X5，X6，X7，X8（绝对值大），所以可以解释为耐力因子（长跑好），而f2则相反。
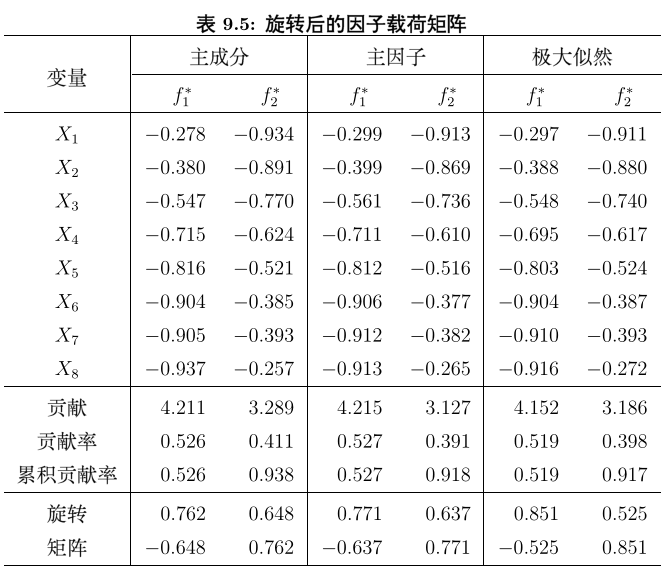
综上，用主成份分析法的因子分析就完整结束，这里需要提及的是，对筛选因子还有主因子法和最大似然法，但具体算法比较复杂，至于本人会不会继续研究还待定，但这三种方法得出的结论是相近的。
ps：本博客的数据和图片均来自薛毅老师的著作《统计建模与R软件》一书，在此表示感谢，若有侵权，马上筛除（应该不会，大家只是用于学习的啦）。