
目录
- 一. 拉普拉斯矩阵性质
- 二. 拉普拉斯矩阵与图分割的联系
- 三. Ratiocut
- 四. 总结
一. 拉普拉斯矩阵性质
这篇文章可能会有些枯燥,着重分享了谱聚类的原理中的一些思想,以及自己本人对谱聚类的一些理解。如果在看完这篇文章后,也能解决你对谱聚类的一些疑问,想必是对你我都是极好的。在之前查阅了很多关于谱聚类的资料,博客,但是发现有些地方仍不是很明白,比如为什么用拉普拉斯矩阵L的特征向量就能表示一个样本,为什么L总会有个最小特征值是0等。
前文简略的介绍了如何将所有样本X构建成拉普拉斯矩阵,利用拉普拉斯矩阵对样本点X进行合适大小的分割,此分割不需要类标,所以是无监督分割。那么这其中具体的原理是什么呢?为什么将n个d维度的样本Xi构建成了相似度矩阵后,构建拉普拉斯矩阵L,就能通过求解L矩阵特征向量后,用特征向量表示Xi,进行kmeans聚类表示Xi的聚类效果呢?
这里我们要知道,拉普拉斯矩阵是基于样本Xi之间构建的相似度矩阵构建的,所以拉普拉斯矩阵相当于是一个图G(V,E),该矩阵(及改图)包含了各个样本点,以及样本点之间的联系的信息。假设有6个样本点,通过构建相似度矩阵,生成了拉普拉斯矩阵,有些样本点是没有联系的,如图一:
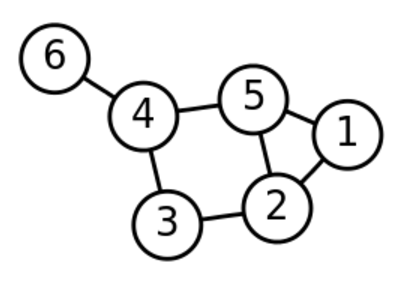
我们想要对图中的节点进行分割归类,得到一个比较合理的样本分割。
分割成如图二的效果:
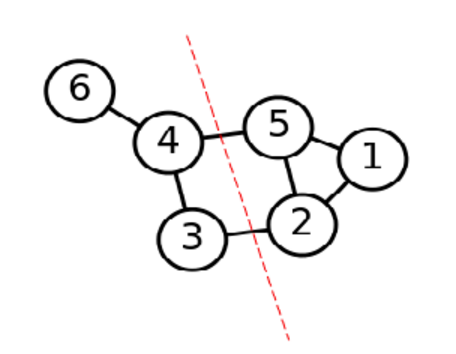
不得不感叹前辈们的聪明智慧,将一个表示样本点联系的图分割,通过拉普拉斯矩阵转换成了矩阵求解的问题。先别着急想拉普拉斯矩阵L与图像分割有什么联系,我们先单纯的从数学角度来L矩阵有什么性质。假设一共有n个样本Xi,现已知得到样本点构建的相似度矩阵S(本章不在此展开,构建相似度矩阵有很多种方式,比如欧式距离,高斯距离等),S是大小为n∗n的矩阵,Sij记录了Xi与Xj样本间的联系。通过相似度矩阵S构建邻接矩阵W(这里构建W的方式也有很多,比如K近邻,全连接构建W等),通过Wij创建对角度矩阵D,大小为n∗n,其中对角线元素,其余位置Dij=0。构建了相似度矩阵W和度矩阵D后,就得到了拉普拉斯矩阵L=D−W。
我们发现L矩阵是一个全对称矩阵,对角线元素是度矩阵中对应的Dij(i=j),其他位置的元素Lij=−Wij(i�=j)。
1. 拉普拉斯性质一
该矩阵第一个性质,任意一个1∗n维的f向量,我们都能得到如下公式,具体推导如公式一:
f′Lf=f′Df−f′Wf=∑i=1ndifi2−∑i,j=1nfifjwij=21(∑i=1ndifi2−2∑i,j=1nfifjwij+∑j=1ndjfj2)=21∑i,j=1nwij(fi−fj)2
性质有什么用呢,举个例子,我们知道L是一个矩阵,假设该L代表的样本Xi是全连接的,一个类。f是任意一个向量,其实Lf=λf,即λ是L的特征值,而f是L的特征向量。所以f’Lf=f’λf=λf’f,而f’∗f是一个常数,所以我们会发现f’Lf是一个定值,假如λ=0,则f’Lf=0,求出来的f就是L对应特征值为0的特征向量。根据性质一,我们会发现Wij>0,则要想f’Lf=0,必须有fi=fj。我们发现Xi的真实情况是都在一类中,而求出来的f’Lf=0中的特征向量有fi=fj这个性质。我们可以将真实情况中Xi彼此为一类的现象与L的0特征值对应的fi=fj这个性质联系,发现二者始终同步且二者只能互相依存。所以在此,我们可以设置拉普拉斯矩阵L的0特征值对应的特征向量f为全1向量,可以用fi在某种程度代表Xi。求出的L的0特征值对应特征向量fi=fj,刚好可以代表Xi与Xj都是同一类。
2. 拉普拉斯矩阵性质二
拉普拉斯矩阵L求出的0特征值个数即对应有几个聚类。聚类间的Xi互不联系。
之前假设的是L中n个样本点全是一类,这是极特殊的现象,一般情况中假设L中有k个部分L1,L2,...Lk,这样的矩阵Li中的元素互为同一类,如图三所示:
L=⎝⎜⎜⎛L1L2⋱Lk⎠⎟⎟⎞
在这种理想情况下,我们已知有k个聚类,而聚类之间元素没有联系,置为0。L矩阵除了对角的L1,L2,...,Lk矩阵以外的位置上元素都是0。我们发现求出L对应的0特征值个数k,即代表了整个图中聚类的个数。求出对应每个0特征值对应的特征向量fi可以做Xi样本的聚类指示器。eg:假设L是一个77的矩阵,其中L1是个33的矩阵,那么代表X1,X2,X3是同一类,则求出L的其中一个0特征值,与之对应的特征向量可以表示为f1=[1,1,1,0,0,0,0]。通过该0特征值对应的特征向量,我们可以看见f中为1的下标对应的样本Xi在同一类。
当然上述只是一种理想情况,在已知聚类结果的条件下,构建了此拉普拉斯矩阵L,让不在同一类的样本W_ij=0。得到0特征值对应特征向量做指示器,未免有些马后炮的感觉。但是在此,我们也有了一个发现,就是拉普拉斯矩阵L的特征向量,在一定程度上可以表示样本Xi。
3. 拉普拉斯矩阵性质三
拉普拉斯矩阵L至少有一个特征值为0。
通过性质二,我们很容易发现,一个L代表的样本Xi,至少也会有一个类,也就是Xi与Xj之间互相都有联系,Lij>0。所以根据性质二反推,则一个拉普拉斯矩阵L至有一个特征值为0。
二. 拉普拉斯矩阵与图分割的联系
介绍完了拉普拉斯矩阵的性质后,我们来讲下拉普拉斯与图分割的联系。
在开始我们交代过,有6个样本点,我们用图来表示这6个样本点,希望能通过图分割出比较好的几个部分,即代表了这几个样本点的聚类。图四就是我们想要的比较好的分割效果:
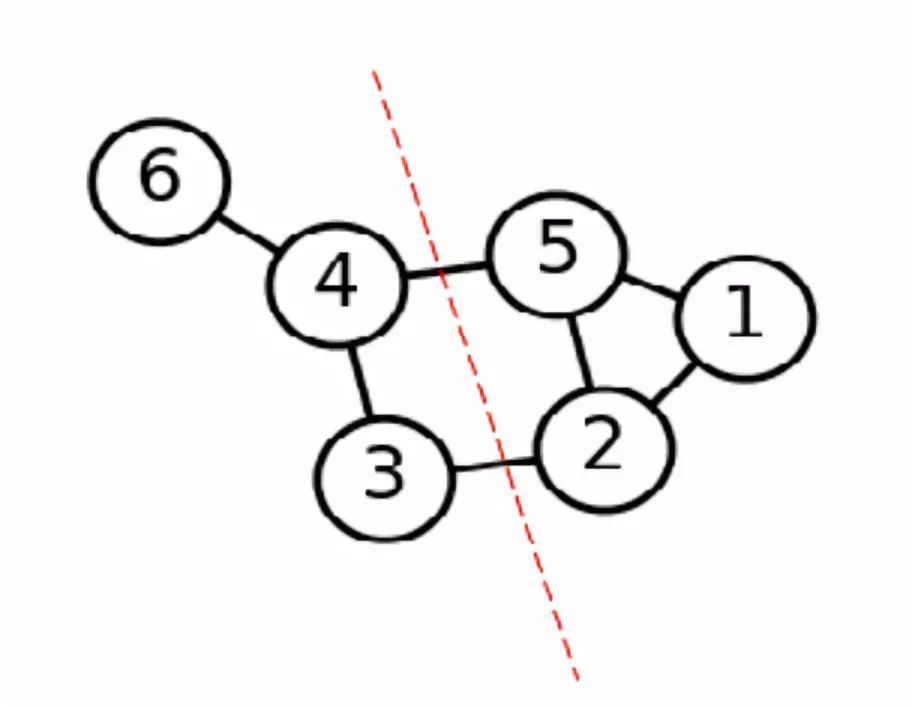
我们希望将所有样本点分成A1,A2,...,Ak个部分,我们想要分割的代价最小,用如下公式表示该分割效果:
cut(A1,A2,⋯,Ak)=21i∑kW(Ai,Ai)
其中我们想要不同类之间有联系的样本点权值相加,切割的部分即这些不同类的样本点之间的边,所以我们想要cut(A1,A2,...,Ak)最小。但是我们会发现,这种策略下的分割很容易造成分割不均匀的现象,如图五所示:
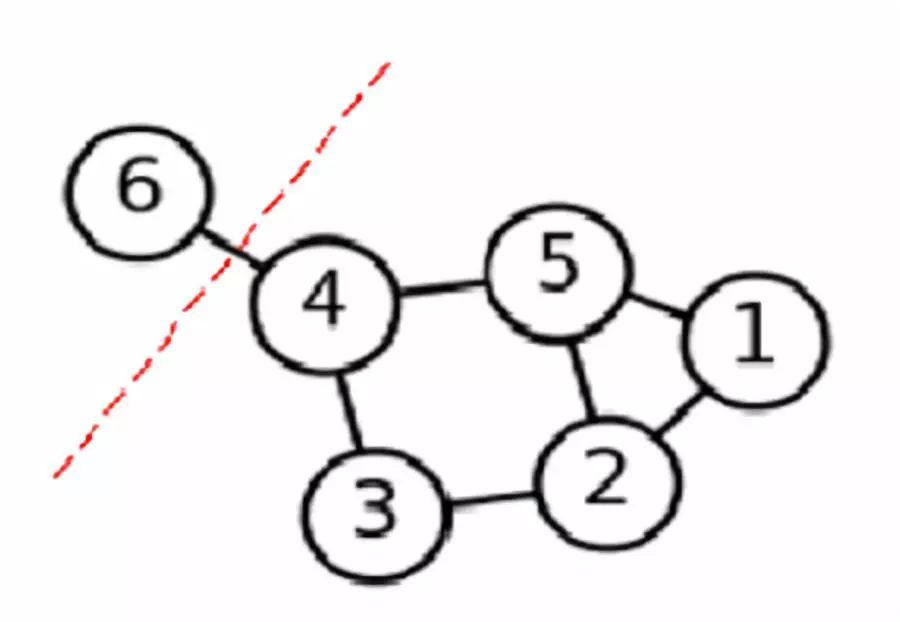
图五这样的切割结果不是我们想要的分割结果,虽然分割的cut(A1,A2,...,Ak)最小,但是会造成分割出很多单个离散的样本点作为一类,分割的类别不均匀。因此,我们提出了Ratiocut和Ncut两种能够均匀地切割图的方法,分别如公式三所示:
Ratiocut(A1,A2,⋯,Ak)=21∑ik∣Ai∣W(Ai,Ai)Ncut(A1,A2,⋯,Ak)=21∑ikvol(Ai)W(Ai,Ai)
其中Ratiocut中|Ai|代表Ai类别中样本点的个数,Ncut中vol(Ai)代表Ai类别中所有边的权重和。两种切割方法都能很好的抑制样本被过于极端的分割造成分割不均匀的现象。
三. Ratiocut
1. L的特征向量h(指示器)
关键来了,拉普拉斯矩阵跟Ratiocut或者Ncut有什么联系呢?在这里我们以Ratiocut为例,我们想要minRatiocut(A1,A2,...,Ak)。和上文中的L向量的特征向量f(做指示器)一样,现在引入A1,A2,...,Ak的指示向量hj=[h1,h2,...,hk],其中j=1,2,...,k,其中hj的具体表达如公式四所示:
hj,i={∣Aj∣1,0, if vi∈Aj if vi∈/Aj
由拉普拉斯性质二最后得到的心得可以看到,在这里我们可以让hj中的h1,h2等可以分别表示样本X1,X2等,并且hj∗1=0。这里要注意hj表示的是Aj类别的指示器,hj中的数值只能表示在Aj中(1/(∣Aj∣)),和不在Aj中(0),所以hj指示器只能局限的表示所有样本是否在一种类别Aj上,不能表示样本与别的类别Ai之间的联系。我们需要更多的指示器hi来表示样本点与别的各类别之间的关系。
2. 拉普拉斯矩阵min(f’Lf)等价min Ratiocut(Ai,~Ai)
指示器hj是一个向量,那么可以利用拉普拉斯矩阵性质一,用hj向量来进行推导。推导过程公式五六所示:
hiTLhi=hiT(D−W)hi=hiTDhi−hiTWhi=m=1∑m=1n=1∑nhi,mhi,nDm,n−m=1∑n=1∑hi,mhi,nwm,n=m=1∑m=1hi,m2Dm,m−m=1∑n=1∑hi,mhi,nwm,n=21(m=1∑2hi,m2Dm,m−2m=1∑hi,mhi,nwm,n+n=1∑hi,n2Dn,n)(5)
hiTLhi=21(m=1∑2hi,m2Dm,m−2m=1∑n=1∑hi,mhi,nwm,n+n=1∑hi,n2Dn,n)=21(m=1∑n=1∑hi,m2wm,n−2m=1∑n=1∑hi,mhi,nwm,n+n=1∑m=1∑hi,n2wn,m)=21m=1∑n=1∑wn,m(hi,m−hi,n)2(6)
这里推导过程于拉普拉斯的性质一推导相同,我们设定了hj中的值,将hj替换成设定的值,继续化简,会发现化简到最后就是Ratiocut。
hiTLhi=21m=1∑n=1∑wm,n(hi,m−hi,n)2=21⎝⎛m∈A,n∈Ai∑wm,n(∣Ai∣1−0)2+m∈Ai,n∈Ai∑wm,n(0−∣Ai∣1)2⎠⎞=21⎝⎛m∈A,n∈Ai∑wm,n∣Ai∣1+m∈Ai,n∈Ai∑wm,n∣Ai∣1⎠⎞=21(cut(Ai,Ai)∣Ai∣1+cut(Ai,Ai)∣Ai∣1)=∣Ai∣cut(Ai,Ai)=Ratiocut(Ai,Ai)
我们发现设定一个指示器hj,拉普拉斯矩阵L表示Xi,hj做拉普拉斯矩阵L的特征向量后,根据L的性质一,竟然hi’Lhi=Ratiocut(Ai, Ai)。也就是说,我们可以将求解拉普拉斯矩阵性质一与Ratiocut(Ai,~Ai)等价。成功的将最小切割图问题转化成了求解矩阵特征向量的问题。之前我们说了,hj指示器中的值只能表示所有样本点是否在类别Aj的关系,需要更多的指示器hi来表示所有样本点跟别的类别的关系。而h_j对于拉普拉斯矩阵L,是L的特征向量。所以需要更多的hi就转换成了需要L更多的特征向量。根据min(hi’∗L∗hi)=min(hi’∗λ∗hi)=min(λhi’∗hi)=min (λ*常数),求解多分类的极小化问题转换成了如下所示,约束条件由开始设定hj’∗1向量=0.得:
argminHTr(HTLH), s.t. HTH=I
我们需要最小的特征值,而L矩阵最小的特征值必为0,对应特征向量是全1向量,对于预测所有样本与类别Ai间的联系没有帮助,所以我们求得倒数二小的特征值开始的前k个特征值对应的特征向量做指示器,因为每个L的特征向量都是对某一类的指示,所以现在要聚k个类,我们就讲这前k个特征向量组成一个矩阵,大小为n∗k。其中每一列是特征向量hi,每一行i有k个位置,分别代表h1,h2,...,hk指示器对该样本Xi与不同类别A1,A2,...,Ak的关系,间接表示一个样本,这样我们就可以通过前k个特征向量表示每个样本Xi后,用K-means对这些间接表示的样本进行聚类。(这其中放宽了公式八多分类的约束条件,因为公式八是hj中是离散数值,这样会造成NP-hard问题)最终,前辈们成功的将图分割问题与求解拉普拉斯矩阵L的特征向量成功联系在一起,给前辈们一个赞!Ncut原理也与Ratiocut类似,在此不重复介绍。
3. 疑问
不过在整个推理谱聚类的过程中还存在一个问题,没有搞明白,谱聚类中核心是对拉普拉斯矩阵进行特征分解,求其最小k个特征向量,用这些特征向量降维表示Xi,然后kmeans聚类。但是如公式八所示,最小化图分割问题里,求解出来的特征向量是有约束条件的,怎么能保证求得的倒数k个小特征值对应的特征值向量hi就一定满足hi∗1=0呢?
四. 总结
拉普拉斯矩阵L有很多特殊的性质,通过这些性质我们发现了L矩阵的特征向量中每个元素i可以一定程度上与表示样本Xi。通过这个特性,前辈们成功的通过求解L的k个特征向量,综合来表示样本Xi,等价求解将整个图的最小化分割问题。所以,可以说拉普拉斯矩阵的作用是对所有样本进行了降维表示,因为是用特征向量表示,所以整个图拉普拉斯矩阵在用k个特征向量表示后也保留了很多关键信息,最后通过kmeans对这些降维后的Xi进行聚类。
对深度学习感兴趣,热爱Tensorflow的小伙伴,欢迎关注我们的网站!http://www.panchuang.net 我们的公众号:磐创AI。