线性判据与回归
线性判据基本概念
生成模型
给定训练样本{(x_n)},直接在输入空间内学习其概率密度函数p(x)
优势
- 可以根据p(x)采样新的样本数据(synthetic data)
- 可以检测出较低概率的数据,实现离群点检测(outlierdetection)
劣势
- 高维下,需要大量的训练样本才能准确估计p(x),否则出现维度灾难问题
判别模型
判别模型:给定训练样本{(x_n)},直接在输入空间内估计后验概率$p(C_i|x)
优势
- 快速直接、省去了耗时的高维观测似然概率估计
线性判据
定义
如果判别模型f(x)是线性函数,则f (x)为线性判据
优势
计算量少,适用于训练样本较少的情况下
模型

判别式
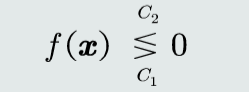
决策边界
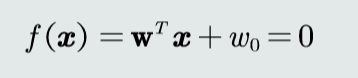
其中w是决策边界法向量,样本到决策边界的距离(r=frac{f(x)}{||w||})
并行感知机算法
目标
学习参数w和(w_0)
预处理
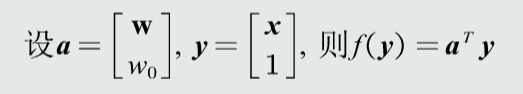

目标函数

梯度下降法,更新参数a
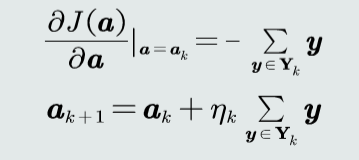
算法流程

串行感知机算法
训练样本串行给出
目标函数
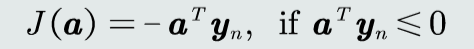
算法流程

Fisher线性判据
找到一个最合适的投影轴,投影后,使得不同类别样本分布的类间差异尽可能大,同时使得各自类内样本分布的离散程度尽可能小
目标函数

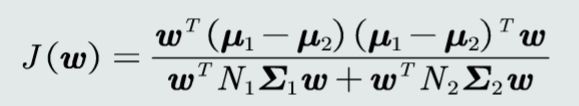
类间散度和类内散度

求解w和(w_0)
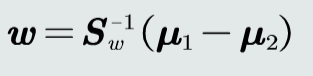
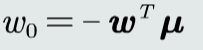
Fisher线性判据
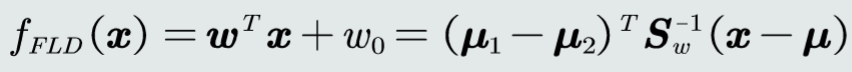
决策边界

支持向量机(SVM)
给定一组训练样本,使得两个类中与决策边界最近的训练样本到决策边界之间的间隔最大
间隔的定义
- 在两个类的训练样本中,分别找到与决策边界最近的两个训练样本,记作(x_+)和(x_-)
- (x_+)和(x_-)到决策边界的垂直距离叫作间隔,记作(d_+)和(d_-)
支持向量(support vector)
- 决策边界记作(Π),平行于11且分别通过(x_+)和(x_-)的两个超平面记作(Π_+)和(Π_-),称为间隔边界
- 位于(Π_+)和(Π_-)上的样本则称为支持向量
目标函数
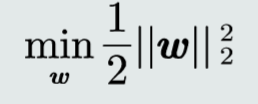
约束条件
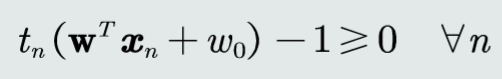
拉格朗日乘数法
等式约束问题的转换

不等式约束问题的转换
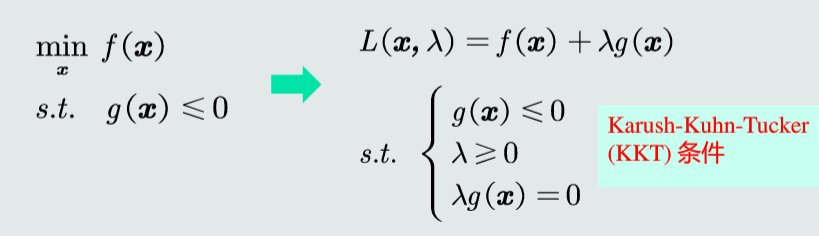
拉格朗日对偶问题
将原问题转化为等价优化问题

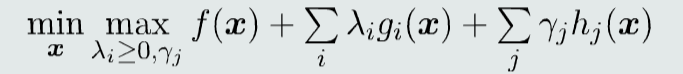
对偶函数
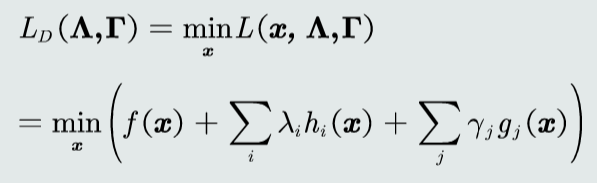
对偶问题
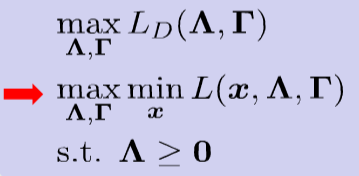
弱对偶性
- 设对偶问题的最优值为 d,主问题的最优值为 p
- 对于所有的优化问题都存在 d* <= p*
强对偶性
- d* = p*
- 强对偶成立条件:
- f(x) 是凸函数
- g(x) 是凸函数
- h(x) 是仿射函数
- 在可行域至少有一点使得不等式约束严格成立
支持向量机学习算法
构建拉格朗日函数
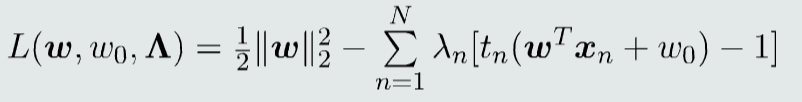
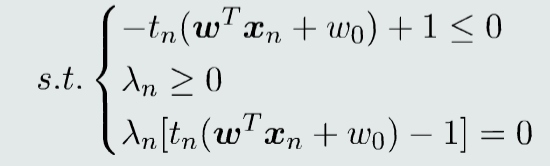
构建对偶函数
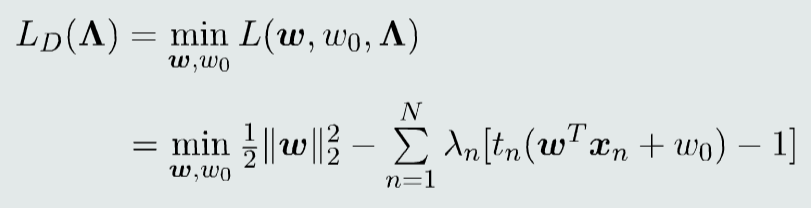
(L_D)对w和(w_0)求偏导,并设偏导等于0,再将结果代入,从而消去w和(w_0)
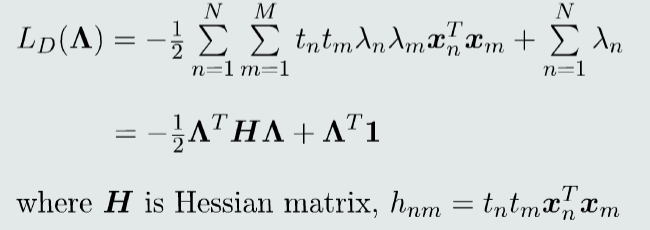
对偶问题

- 该问题为标准的二次规划问题,可调用软件函数求解
求解支持向量
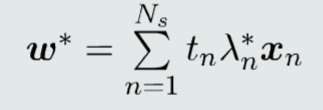

识别决策