【欧几里得算法】辗转相除法
1.被整除数的性质:若c|a,c|b,则c|(ma+nb)
整除数的性质:若a|c,b|c,gcd(a,b)=1,则ab|c。(否则lcm(a,b)|c)
2.gcd的定义
若c|a,c|b,则c为a和b的公因数。当c能被a和b的所有公因数整除时,c是a和b的最大公因数,记为gcd(a,b)。
若c|gcd(a,b)的充要条件是c|a&&c|b。
带余除法:a=bq+r,证明常用。
当gcd(a,b)=1时,称a和b互素。
最小公倍数lcm(a,b)=a*b/gcd(a,b)。
3.证明:gcd(a,b)=gcd(b,a%b)
a可以表示成a=k*b+r,其中r=a%b。
假设d|a,d|b,则r=a-k*b,r/d=a/d-k*b/d=m,m为整数,故d|r。
所以若d是a和b的公因数,则d也是b和a%b的公因数。
必要性同理易证。
4.辗转相除法:根据3递归,终止于gcd(a,0)=a。
更相减损术:gcd(a,b)=gcd(b,a-b)。
感性理解:gcd(a,b)是组成a和b的基本单位,相减或相除都一定不会丢失,直到不能进行为止就是答案。

ll gcd(ll a,ll b) {return b==0?a:gcd(b,a%b);} ll lcm(ll a,ll b) {return 1ll*a/gcd(a,b)*b;}
另外,gcd可以O(n^2)批量预处理。
5.最大公因数gcd的相关推论
(1)转为互素:gcd(a,b)=d的充要条件是gcd(a/d,b/d)=1
数乘:若gcd(a,b)=d,则gcd(ka,kb)=kd。
(2)gcd乘法:gcd(a1,b2)*gcd(b1,b2)=gcd(a1b1,a1b2,a2b1,a2b2)
(3)消除:若gcd(a,c)=1,则gcd(ab,c)=gcd(b,c)
6.相减树理论:根据更相减损术的推广,若干数字的gcd可以转化为这些数的相减树+任意一个原数字,如gcd(a,b,c,d,e)=gcd(a-b,b-c,c-d,d-e,e)。
感性理解,只要有一个原数就可以通过相减树得到其它所有数字,辗转相除同理,虽然不能还原出原数,但是信息全部继承了。
7.大量gcd求解技巧:设b[x]表示数列中有多少数字是x的倍数,求解b[x]可以O(n ln n)枚举每个数字的倍数或者O(n log n)线性筛后对每个数分解素因数。
序列中公因数有x的子集个数是2^b[x]-1,运用容斥原理即可得到gcd为对应数字的子集个数。
8.容斥:求所有满足是给定的n个数字的倍数的数字的信息,从最大数字m枚举到1,每次将
例题:【SRM20】数学场
9.辗转相除法对于负数:会得到两个数的gcd,但正负不确定。
辗转相除法对于0:会得到另一个原数。
【扩展欧几里德算法】(不定方程,模线性方程)
参考:jumping_frog(扩欧)
刘汝佳《算法竞赛入门经典 第二版》
【基本算法】对于不完全为 0 的非负整数 a,b,gcd(a,b)表示 a,b 的最大公约数,必然存在整数对 x,y ,使得gcd(a,b)=ax+by。
证明:设 a>b。
1,显然当 b=0,gcd(a,b)=a。此时 x=1,y=0;
2,ab!=0 时
设 ax1+by1=gcd(a,b);
bx2+(a mod b)y2=gcd(b,a mod b);
根据朴素的欧几里德原理有 gcd(a,b)=gcd(b,a mod b);
则:ax1+by1=bx2+(a mod b)y2;
即:ax1+by1=bx2+(a-(a/b)*b)y2=ay2+bx2-(a/b)*by2;
根据恒等定理得:x1=y2; y1=x2-(a/b)*y2;
这样我们就得到了求解 x1,y1 的方法:x1,y1 的值基于 x2,y2.
上面的思想是以递归定义的,因为 gcd 不断的递归求解一定会有个时候 b=0,所以递归可以结束。

void gcd(ll a,ll b,ll& d,ll& x,ll& y) { if(!b){d=a;x=1;y=0;} else{gcd(b,a%b,d,y,x);y-=x*(a/b);} }
上面求出ax+by=gcd(a,b)的一组解(x1,y1),任取另外一组解(x2,y2),令g=gcd(a,b),则有:
ax1+by1=ax2+by2
a(x1-x2)=b(y2-y1) 两边同除以g
a'(x1-x2)=b'(y2-y1) 此时a'与b'互素,因此(x1-x2)一定是b‘的整数倍
x1-x2=kb' 代入得 y2-y1=ka'
注意上述推导并没有用到ax+by的右边是什么,也就是说只要求出一组解就可以写成任意解,一切都只需要求出一组解。
结论:设a,b,c为任意整数,若方程ax+by=c的一组整数解为(x0,y0),则它的任意整数解都可以写成(x0+kb',y0-ka'),其中a'=a/gcd(a,b),b'=b/gcd(a,b),k取任意整数。
所以一定要先求出特解(利用右边),然后纯粹利用左边求出通解,在下面不定方程的求解中这个顺序尤为重要。
注意:再次强调,扩欧只能用于求解ax+by=gcd(a,b),特殊地,用于求解a'x+b'y=1(a'与b'互质)。
【应用一:求解不定方程】
(丢番图方程) ax+by=c 求解步骤:
1.求g=gcd(a,b)。
2.若c%g≠0,方程无解。(扩欧只能求解ax+by=gcd(a,b)的整数解,如果整体乘上c/gcd(a,b)后不是整数了就无解,开始先同除g方便操作)
3.方程两边同时除以g,得到a'x+b'y=c'。(此方程完全等价,因为解没有变化)
4.通过扩展欧几里德算法求解a'x+b'y=1的一组解(x0,y0)
5.得到原不定方程的一组解(X=x0*c',Y=y0*c')
6.得到原不定方程通解(X+kb',Y-ka')注意一正一负
7.得到最小非负整数解:x=((X%b‘)+b’)%b‘ , y=((Y%a’)+a‘)%a’(+a或b转为正数)
PS:x、y可能为0,若要求正解要再次特判+a或+b。
PPS:除以g是为了方便计算,对解没有影响。除以g后扩欧只能计算a'x+b'y=1的方程,这时候解就要乘c/g得到原解。
PPPS:一个问题
{
求解不定方程时,我们通过ax+by=gcd(a,b)整体扩大c/gcd(a,b)倍来得到方程ax+by=c的解。
对于ax+by=gcd(a,b),通解是(x0+ka/g,y0-kb/g),所以我之前以为ax+by=c的通解应该由ax+by=gcd(a,b)的每一个解扩大c/gcd(a,b)得到。
换句话说,我以为ax+by=c的通解是(c/g*(x0+ka/g),c/g*(y0-kb/g)),后来发现我错了。
紫书中有句不起眼的话:“注意,上面的推导过程并没有用到“ax+by”的右边是什么”。
所以,ax+by=c的通解同样是(x0+ka/g,y0-kb/g),而(c/g*(x0+ka/g),c/g*(y0-kb/g))会让通解的数量减少。
那为什么之前会有错误的认识呢?其实(c/g*(x0+ka/g),c/g*(y0-kb/g))没有包含的那些通解就是除以c/g后不是整数的解。
换句话说,ax+by=gcd(a,b)中的有一些非整数解,扩大c/gcd(a,b)倍后就变成了ax+by=c的整数解。
综上,ax+by=c的通解求法是先求特解(X=x0*c/gcd(a,b),Y=y0*c/gcd(a,b)),后求通解(X+kb'/g,Y-ka'/g)。
}
//???紫书中似乎提到一个扩欧解x0,y0的特性:“x可能为负数,但因为|x|+|y|最小,所以加上n以后一定非负”???
【应用二:模线性方程组】
---
题外话:
减法取模:(a-b)%n=((a%n)-(b%n)+n)%n 注意加n
大整数取模:自左向右逐个加入,每次乘10后取模。
幂取模:快速幂运算
---
目标:给定a,b,n,解方程ax≡b(%n)。
a≡b(%n)的含义是“a和b除以n的余数相同“,其充要条件是”a-b是n的整数倍“。
eg. a mod 3 = 1等价于a≡1(mod 3)等价于a-1=k*3。
---
同余性质证明模板:
性质:如果a≡b(mod m),x≡y(mod m),则a+x≡b+y(mod m)。
证明:条件告诉我们,可以找到p和q使得a-mp = b-mq,也存在r和s使得x-mr = y-ms。于是a-mp + x-mr = b-mq + y-ms,即a+x-m(p+r) = b+y-m(q+s),这就告诉我们a+x和b+y除以m的余数相同。
---
同余性质:
1.支持同余数的两边同加减乘幂,对于同余运算来说重要的只有余数部分,无关整的部分。
2.除法:若ac≡bc(%m),c≠0则a≡b(% m/gcd(c,m) )其中gcd(c,m)表示c,m的最大公约数 (简证:g=gcd(c,m),ac'g-bc'g=k*m'g,约去g,则可得到特殊情况。)
所以,同余符号左右和模数可以同时除以公约数。
特殊地 ,gcd(c,m)=1则a≡b(%m)
{证明:g=gcd(c,m)
ac'g-bc'g=k*m'g,约去g,得到ac'-bc'=k*m'那么得到特殊情况ac≡bc(%m),gcd(c,m)=1。
ac-bc=k*m即(a-b)c=k*m,由于c与m互质,则(a-b)=k*m即a≡b(%m),得证。
}
3.若a ≡ b (mod m),n|m,则 a ≡ b (mod n)
若a ≡ b (mod mi) (i=1,2...n) 则 a ≡ b (mod [m1,m2,...mn]) 其中[m1,m2,...mn]表示m1,m2,...mn的最小公倍数
---
ax≡b(%n)
ax-b=ny即ax-ny=b。令g=gcd(a,n),方程有解当且仅当g|b。
同除以g,得a'x-n'y=b'。
利用扩欧解a'x-n'y=1,本质上是在解ax≡g(%n),此时的解距离x0还差b/g倍。
x0=(x*b/g)%n,xi=x0+k*(n/g)。
1.证明方程有一解:当g|b时,x为ax≡g(%n)的解,则x0=(x*b/g)%n为ax0≡b(%n)的一解。
2.证明方程有g个解:一解相当于一个同余等价类,x0等价于所有x%n=x0的解x,这里有g个解是指有g个同余等价类。(我觉得紫书中也是这个意思,但非要用y来说明,令人浮想联翩……)
首先证明xi=x0+k*(n/g)也是方程的解,前已证得x0为ax0≡b(%n)的一解,则:
axi=a(x0+k*n/g)(%n)=ax0+ak*n/g(%n) 由于g|a即a'=a/g,所以axi=ax0(%n),得证。
然后显然xi至多有g个,k的取值为0~g-1。当k≥g时,k=(g*[k/g]+k%g),[k/g]*(g*n/g)部分可以约去,则实际上与0~g-1等价。
3.解的间隔显然是n/g。
特别注意:大多数题目要求的解是非负数或正数,而扩欧解出来不一定是!!!
【乘法逆元(a-1)】
逆元详解 by ACdreamer
乘法逆元小结 by Tuesday..
乘法逆元:方程ax≡1(%n)的解称为a关于模n的逆(记得模n)。当gcd(a,n)=1时,该方程有唯一解(同余等价类);否则,该方程无解。
可以理解为倒数,a*x模n下等于1。在模n意义下,除以a等价于乘a的逆元,即a^(-1)≡a^(φ(n)-1) (%n)。
求逆元的方法:O(log(n))
前提:gcd(a,n)=1即a,n互素。
1.若n为素数(n=p),则由费马小定理a^(p-1)≡1(%p)得x=a^(p-2)%p。
2.若n不为素数,则由欧拉定理a^φ(n)≡1(%n)的x=a^(φ(n)-1)%n。
3.前两种方法需要快速幂运算,为了方便也可以直接用扩欧解ax-ny=1得到的解x即为逆元。
5.对于x=a!/b!(%p),b!|a!,若gcd(b!,p)>1,可以使用中国剩余定理求解(不会爆数据),过程见下面“中国剩余定理”。

ll inv(ll a,ll n) { ll d,x,y; gcd(a,n,d,x,y); //return d==1?(x+n)%n:-1; return (x%n+n)%n; }
<线性求1~n的乘法逆元及其应用>
乘法逆元函数inv(x)是完全积性函数,即inv(xy)=inv(x)*inv(y)或(xy)^(-1)=x^(-1)*y^(-1) (%p)。
过程:
1.过程中所有数都mod p,实际上在模运算中只要不涉及除法都可以模。
2.首先求出1!,2!,...,n!的值并记录,然后求出n!的逆元。
由与逆元是积性函数,有:
(n!)^(-1)=(n-1)!^(-1)*n^(-1),移项得
( (n!)^(-1) )/( n^(-1) ) = (n-1)! ^ (-1)
根据除以一个数等价于乘以这个数的逆元
(n!)^(-1)*n=(n-1)^(-1)
从而逆向求出1!,2!,...,n!的逆元。
3.接下来利用阶乘的逆求出每个数的逆。
( (n-1)! ^ (-1) ) * n ^ (-1) = (n!) ^ (-1) 移项得
n ^ (-1) = ( (n!) ^ (-1) ) / ( (n-1)! ^ (-1) )
根据除以一个数等价于乘以这个数的逆元
n^(-1)=(n!)^(-1)*(n-1)!
注意,两次变换都是根据(n!)^(-1)=(n-1)!^(-1)*n^(-1)【(n!)-1=((n-1)!)-1*(n)-1】进行的(不同的数字除过去),这基于乘法逆元是积性函数。

void gcd(int a,int b,int &x,int &y) { if(b==0){x=1;y=0;} else{gcd(b,a%b,y,x);y-=x*(a/b);} } void pre_inv() { fac[0]=fac[1]=1; for(int i=2;i<p;i++)fac[i]=(fac[i-1]*i)%p; int xx,yy; gcd(fac[p-1],p,xx,yy); inv[p-1]=((xx%p)+p)%p;//扩欧解不一定是最小非负解! for(int i=p-2;i>=0;i--)inv[i]=(inv[i+1]*(i+1))%p; }
【欧拉函数(phi)】
参考:欧拉函数 by handsomecui
欧拉函数求法与应用 by sentimental_dog
1.定义欧拉函数φ(n)表示1~n中与n互素的数的个数。
φ(x)=x(1-1/p(1))(1-1/p(2))(1-1/p(3))(1-1/p(4))…..(1-1/p(n)) 其中p(1),p(2)…p(n)为x的所有素因子
欧拉函数数列:1 1 2 2 4 2
公式的简单理解:对于每个素因子pi,x范围内pi的倍数有x/pi个,即不含pi的有x*(1-1/pi),连乘起来即可。
2.性质:
(1)对于质数p,φ(p)=p-1,φ(p^k)=p^k-p^(k-1)=(p-1)p^(k-1)。(p^(k-1)个p)
(2)欧拉函数是不完全积性函数——若m,n互质,φ(mn)=φ(m)φ(n)。
3.公式:n=∑d|nφ(d)
证明:考虑n的所有数字x∈[1,n],有(n,x)=d即(n/d,x/d)=1,所以满足(n,x)=d的所有的x的个数为φ(n/d),那么所有n的因子的φ就是答案。
4.公式:1~n中与n互质的整数和是为( n*φ(n)+[n=1] )/2,证明:gcd(n,i)=gcd(n,n-i),所以互素数总是成对出现。(但约数和不是n*(n+1)/2-n*φ(n)/2+1……)。
5.求Σgcd(i,n),i=1~n
解:设g(i)=gcd(i,n),显然g(i)是积性函数。积性函数得前缀和也是积性函数,所以f(n)=Σgcd(i,n),i=1~n也是积性函数,由唯一分解定理:
f(n)=f(p1^a1)*...*f(pk^ak)
又因为f(n)=Σd|nφ(d)*n/d(参考n=∑d|nφ(d)的证明,所有φ(d)的gcd是n/d)
所以f(p^k)=p^k+(p-1)p^0 * p^(k-1) + (p-1)p^1 * p^(k-2) + ... + (p-1)p^(k-1) * p^0=(p-1)*p^(k-1)*k+p^k

int get_phi(int n) { //phi(n)=n*(1-1/p1)*(1-1/p2)...*(1-1/pk) int m=(int)sqrt(n+0.5); int ans=n; for(int i=2;i<=m;i++) if(n%i==0) { ans=ans/i*(i-1);//在允许的情况下,先除后乘避免爆范围 while(n%i==0)n/=i; } if(n>1)ans=ans/n*(n-1); return ans; }
【欧拉定理&费马小定理】
欧拉定理:a,n为正整数且互素,a^φ(n)≡1(%n)
费马小定理:p为素数,a^(p-1)≡1(%p)
★重要应用:简化幂的模运算 a^b=a^(b%φ(p)) mod p
例如: 计算 7^222的个位数,实际上是求7^222被10除的余数。
且7与10互质,φ(10)=1,由欧拉定理知7^4= 1mod 10
故7^222=(7^4)^55*(7^2)=>(1^55)*(7^2)=>49=>9 mod 10
【欧拉线性筛】
引用自:贾志鹏线性筛
只要一个函数满足三个条件就可以线性筛:
1.p是素数,O(1)求f(p)。
2.f(i)是积性函数
3.f(i*prime[j])可以用f(i)和prime[j]快速算出,其中prime[j]是i的最小素因子。
<素数筛>
本质:每个数字只被最小的素数筛去,把每个数字分解为[素数*倍数]即[prime[j]*i],其中prime[j]为最小素数。
枚举i=1~n,每次选择比i小的素数组合为合数筛选。
if(i%prime[j]==0)break;如果当前素数已经能整除i,则这个倍数i中有质因数prime[j],之后筛的prime[j+1]*i这个数字的最小素数是prime[j],所以后面一定会被prime[j]乘一个倍数筛掉,此时筛就没有必要。

#include<cstdio> #include<algorithm> #include<cstring> const int maxsize=1000010; int n,prime[maxsize],tot; bool mark[maxsize]; int main() { scanf("%d",&n); memset(mark,0,sizeof(mark)); tot=0; for(int i=2;i<=n;i++) { if(!mark[i])prime[++tot]=i; for(int j=1;j<=tot;j++) { if(i*prime[j]>n)break; mark[i*prime[j]]=1; if(i%prime[j]==0)break; } } printf("tot=%d ",tot); for(int i=1;i<tot;i++)printf("%d ",prime[i]); printf("%d ",prime[tot]); return 0; }
找一个数字的所有质因数:记录每个数字的最小素数,然后对目标不断除最小素数就可以得到所有质因数。
线性筛求每个数的每个质因数可以用上面的方法,也可以枚举素数的方数的倍数。下面的方法复杂度也差不多。
遍历每个数字的每个质因数:c[i]记录数字i剩余数字,对每个数字i找其所有倍数j的c[j]除以c[i](c[i]=1就不执行),这样会自然的使用所有素数方数筛选,只不过多一些不影响复杂度的枚举,大概可以跑1千万。
<积性函数>
积性函数:对于所有互质的正整数a和b有f(ab)=f(a)f(b)的数论函数。
完全积性函数:对于所有正整数a和b有f(ab)=f(a)f(b)的数论函数
f(1)=1
1.性质一:对于n=∏pi^ki,有f(n)=∏f(pi^ki)
2.性质二:对于完全积性函数,还有f(n)=∏f(pi)^ki以及f(n^k)=f(n)^k
3.常见积性函数:欧拉函数,莫比乌斯函数,乘法逆元函数等。
4.积性函数的约数和、前缀和也是积性函数。
<欧拉函数>
线性筛欧拉函数本质上是因为欧拉函数是积性函数(但不是完全积性函数)。
欧拉函数是积性函数的原因可以从公式上显然看出。
欧拉函数:φ(x)=x(1-1/p(1))(1-1/p(2))(1-1/p(3))(1-1/p(4))…..(1-1/p(n)) 其中p(1),p(2)…p(n)为x的所有质因数
筛选过程和素数筛十分相似,因为本质上都是根据唯一分解定理,一个数由其最小的素数筛掉,只是过程中顺便求phi。
1.若i为素数,phi[i]=i-1。
2.若i%prime[j]==0,则i中有prime[j],那么phi[i*prime[j]]中有的素数phi[i]都有,差的只是最前面乘的数字多个prime[j],即phi[i*prime[j]]=phi[i]*prime[j]。然后和素数筛一样退出。
3.若i%prime!=0,则i中没有prime[j],那么phi[i*prime[j]]中缺少prime[j],最前面乘的数字多个prime[j],那么就是乘上(prime[j]-1)/prime[j]和prime[j],约分得phi[i*prime[j]]=phi[i]*(prime[j]-1)。

void pre_phi(int x) { phi[1]=1;int tot=0; memset(mark,0,sizeof(mark)); for(int i=2;i<=x;i++) { if(!mark[i]) { prime[++tot]=i; phi[i]=i-1; } for(int j=1;j<=tot;j++) { if(i*prime[j]>x)break; mark[i*prime[j]]=1;//筛 if(i%prime[j]==0){phi[i*prime[j]]=phi[i]*prime[j];break;} else phi[i*prime[j]]=phi[i]*(prime[j]-1); } } }
<莫比乌斯函数>
1.μ(1)=1。
2.x含有奇数个素因子,μ(x)=-1。
3.x含有重复素因子,μ(x)=0。
4.x含有偶数个素因子,μ(x)=1。
显然,μ函数是积性函数,那么根据μ(1)=1和μ(p)=-1(p为素数),可以筛出所有莫比乌斯函数。
另有埃式筛法,μ(x)是其所有因子的μ和取反。
例题:【CodeForces】585 E. Present for Vitalik the Philatelist
<最小素因子幂次>
1.p,d=1
2.i%prime[j],d=1
3.i%prime[j]==0,d=d[i]+1
<约数个数>
1.p,e=2
2.i%prime[j],e=e[i]*e[prime[j]]=e[i]*2
3.i%prime[j]==0,e=e[i]/(d[i]+1)*(d[i]+2)
<约数和>
1.p,f=i+1
2.i%prime[j],f=f[i]*f[prime[j]]
3.i%prime[j]==0,f=f[i]+f[i/mi[i]]*mi[i]*prime[j]
【中国剩余定理(CRT)】
引用自:孙子定理_百度百科
由于公式较多,就直接贴图片了。
详细过程看百科,只要顺序看下来就能理解了,下面的过程是从那里简化的。
中国剩余定理实际上实在求解一元同余方程组(S)

<中国剩余定理的通解>
当m1...mn两两互质时有解,通解可以采用构造法获得。


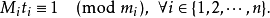 注意此时逆元必定只针对模mi意义下成立(mi之间两两互质)
注意此时逆元必定只针对模mi意义下成立(mi之间两两互质)
方程组(S)的通解形式为:
★在模M意义下只有唯一解: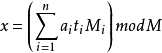
<证明>


由以上两条就很容易看出构造法的神奇了,在%mi意义下,ti*Mi=1(gcd(Mi,mi)=1),而其它ajtjMj由于模数互质无法变1,又因为Mj中含mi而约去,最终剩下ai。
由于mi两两互质,显然下一个解间隔为M,故得证。
★重要应用:处理非互素逆元
【BZOJ】2142 礼物 CRT
【排列组合】
具体内容见计数问题——onion_cyc。
<二项式定理>
观察杨辉三角可以发现,它的第i行的数字是C(i-1,0),C(i-1,1)...C(i-1,i-1),即同一行同下标,上标从0开始递增。
由杨辉三角也可以发现组合数的两大核心性质(同行左右对称,每个数等于上面和上面左边两数之和)。
另一方面,把(a+b)^n展开的多项式系数和杨辉三角一致,由此可得
★二项式定理: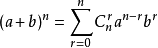
其中组合数对应杨辉三角也对应系数,后边对应项的内容。
也可以理解为n个括号,多少个选a,多少个选b出来的结果。
而求解系数可以使用组合数性质4。
【组合数取模】lucas定理
引用自:lucas_百度百科(证明)
组合数取模 by ACdreamers
证明过程见百度百科,大概是根据二项式定理左右变换后展开推导。
★Lucas定理:C(n,m)=C(n%p,m%p)*C(n/p,m/p) mod p 对于C(n/p,m/p)递归处理。
注意p应是素数。
定理的本质是把n和m看成p进制数,对于C(n,m)%p,如果

则有
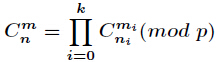

#include<cstdio> #include<algorithm> #include<cstring> using namespace std; const int p=10007; int fac[p+10],inv[p+10]; void gcd(int a,int b,int &x,int &y) { if(b==0){x=1;y=0;} else{gcd(b,a%b,y,x);y-=x*(a/b);} } void pre_inv() { fac[0]=fac[1]=1; for(int i=2;i<p;i++)fac[i]=(fac[i-1]*i)%p; int xx,yy; gcd(fac[p-1],p,xx,yy); inv[p-1]=((xx%p)+p)%p;//扩欧解不一定是最小非负解! for(int i=p-2;i>=0;i--)inv[i]=(inv[i+1]*(i+1))%p; } int C(int n,int m) { if(n<m)return 0; if(n<p&&m<p)return (1ll*fac[n]*inv[m]*inv[n-m])%p; return (C(n%p,m%p)*C(n/p,m/p))%p; } int main() { pre_inv(); int T,n,m; scanf("%d",&T); //for(int i=0;i<10;i++)printf("inv_%d=%d ",i,inv[i]); while(T--) { scanf("%d%d",&n,&m); printf("%d ",C(n,m)); } return 0; } BZOJ 2982
简单总结:
1.模数为素数:lucas
模数分解后无平方因子,直接分开计算素模数lucas后用CRT合并。
2.模数为素数平方:扩展lucas
模数分解后有平方因子,分成若干p^k后提取上下的因子p抵消后快速幂加回。
这种算法称为扩展lucas,再用CRT合并。
lucas的复杂度瓶颈都是模数范围的阶乘预处理,即O(min(n,p)),p是分解后的模数。所以一般用于n太大而p不大的情况。
3.例题:【BZOJ】1485: [HNOI2009]有趣的数列
这题求组合数,p较大且不一定是素数,n较小。
采用的方法是对每个数字分解素因数,统计每个素因子最终的出现次数,分子+分母-,最后直接模p。
有点厉害……
【素数测试】Miller-Rabin算法
引用自:数论部分第一节:素数与素性测试 by Matrix67
当p为素数时,根据费马小定理,有$a^{p-1}=1(\%p)$。
根据Miller-Rabin测试原理,当$x^2=1(\%p)$时,有$x=n-1||x=1$,因为x^2-1=(x+1)(x-1)。
也就是可以提取指数中的因子2,则当$a^{2k}=1(\%p)$时,需要满足$a^k=1(\%p)$或$a^k=p-1(\%p)$。
探测过程:选择一个底数px,分解$n-1=d*2^k$,初始为d每次乘2到n-1为止,每次进行Miller-Rabin测试,最后进行Fermat测试。
底数2,7,61即可探测出所有int范围内的素数。
需要特别注意,选为底数的数字要特判。(2,7,61)

#include<cstdio> const int px[]={2,7,61}; int power(int x,int k,int m){ int ans=1; while(k){ if(k&1)ans=1ll*ans*x%m; x=1ll*x*x%m; k>>=1; } return ans; } bool prime(int n){ for(int i=0;i<=2;i++){ if(px[i]==n)return 1;//!!! int x=n-1; while(!(x&1))x>>=1; int now=power(px[i],x,n),last; while(x<n-1){ last=now;now=1ll*now*now%n;x<<=1; if(now==1&&last!=1&&last!=n-1)return 0;//Miller-Rabin } if(now!=1)return 0;//fermat } return 1; } int main(){ int p;scanf("%d",&p); printf("isprime=%d ",prime(p)); return 0; }
【扩展欧拉定理】
直接看:【CodeForces】906 D. Power Tower 扩展欧拉定理
【莫比乌斯反演】解决因子或素因数个数有关的问题
参考:莫比乌斯反演课件 by PoPoQQQ
★概念:对于函数F(n)=Σd|nf(d)(即满足积性函数),根据莫比乌斯反演定理,可得f(n)=Σd|nμ(d)*F(n/d)或f(n)=Σn|dμ(d/n)*F(d)。(若F(n)可以表示成所有因子f值的和,f值就可以通过F反演得到)
定义:μ(d)为莫比乌斯函数,定义如下:(本质上是一个关于因子的容斥系数函数)
(1) d=1,μ(d)=1
(2) d含重复素因子,μ(d)=0
(3) 否则,设素因子个数为k,μ(d)=(-1)^k
性质:对于任意正整数n,有:
n=1,Σd|nμ(d)=1
n>1,Σd|nμ(d)=0
证明:将n唯一分解,则μ≠0的只有次数为1的因子,组合数带入二项式定理得证(详见课件)。
性质:莫比乌斯函数是非完全积性函数,可以用欧拉线性筛求解。f(1)=1,积性函数的前缀和也是积性函数
莫比乌斯函数可以用于和因子或素因数个数有关的容斥题目。
反演定理形式1:对于函数F(n)=Σd|nf(d),可得f(n)=Σd|nμ(d)*F(n/d)。
证明:
1.f(n)=Σd|nμ(d)*F(n/d)
2.=Σd|nμ(d)*Σk|(n/d)f(k)(由函数F(n)=Σd|nf(d)得到)
3.=Σk|nf(k)*Σd|(n/k)μ(d)
解释:已知k|n,求满足d|n,k|(n/d)的d。
k*x=n/d即k*x*d=n,由k|n得x*d=n/k即d|(n/k)
4.=f(n)(由前面的性质只有k=n时Σd|(n/k)μ(d)结果为1)
反演定理形式2:对于函数F(n)=Σn|df(d),可得f(n)=Σn|dμ(d/n)*F(d)
证明同理,第三步如下:
已知n|k,求满足n|d,d|k的d。
n*x=d d*y=k,两式相乘得n*x*y=k,又n|k,所以x*y=k/n。
由一式x=d/n,代入得y*d/n=k/n即(d/n)|(k/n),故得证。
应用:
1.容斥原理:和素因子个数有关容斥。
例题:【BZOJ】2440: [中山市选2011]完全平方数
2.数对问题
①令f[x]表示满足给定条件的gcd(a,b)=x的数对个数,F[x]表示满足给定条件的满足 x | gcd(a,b) 的数对个数,则F[x]=Σx|df(d)。
易得F[x]=(n/x)*(m/x),那么根据莫比乌斯反演定理,f(x)=Σx|dμ(d/n)*F(d)=Σx|dμ(d/n)*(n/d)*(m/d)。
f(x)=Σx|d μ(d/n) * (n/d) * (m/d),最后由gcd(a,b)=x等价于gcd(a/x,b/x)=1,令n/=x,m/=x就可以对f(1)进行取值分块优化。
②对于gcd(a,b)=x的数对个数,由[gcd(i,j)=1] <=> Σd|i^d|j μ(d),可得
f(x)=Σd<=mins μ(d)*(n/xd)*(m/xd),mins=min(n/x,m/x),可以直接进行取值分块优化。
例题:
(1)【BZOJ】2301: [HAOI2011]Problem b 由Σd|n得到Σt=1~N/d从而分块取值优化
(2)【BZOJ】2820: YY的GCD 多组询问,交换两个Σ的顺序,前面√n回答询问,后面预处理前缀和。
(3)【BZOJ】3529: [Sdoi2014]数表 多组询问,交换Σ,前面√n回答询问,后面预处理前缀和。
(4)【BZOJ】2154: Crash的数字表格 推出前后两次分块取值优化
(5)【BZOJ】2693: jzptab 多组询问,合并前两个Σ,前面√n回答询问,后面预处理前缀和。
公式推导常用技巧:
1.“Σ”的移动与合并。
//2.Σi=1~nΣj=1~i (i,j) <==> [ Σi=1~nΣj=1~n (i,j)+Σi=1~n (i,i) ] /2
3.由Σd|n得到Σt=1~N/d从而分块取值优化
//4.n/a/b <=> n/ab,分块取值优化
5.Σi=1~nΣj=1~m (i,j) <=> Σx=1~nmΣd|x (d,x/d)
6.上界为n,实际只有√n
7.[gcd(i,j)=1] <=> Σd|i^d|j μ(d)
8.f,F可以简单定义为满足指定条件了的数对,第二步反演可以变成,f(x)=Σx|dμ(d/n)*F(d),令i=d/n,f(x)=Σi=1~x/dμ(i)*F(in)。
9.Σd|nμ(d)/d=φ(n)/n
【补充知识】
1.高斯函数(下取整函数)至多有2*√n个取值,即f(i)=[n/i]。
2.调和级数:1+1/2+1/3+...+1/n,数量级为ln n。
3.约数相关:
数字n的约数个数:num=(a1+1)(a2+1)...(ak+1)
1~n中所有数的约数个数和num=[n/1]+[n/2]+...+[n/n],数量级为n ln n,计算O(√n)(见1)。
数字n的约数和约数和:√n
1~n中所有数的约数和num= i * (n/i+1)*(n/i)/2。(O(√n))(枚举约数贡献等差数列)
约数有对应关系,d1*dk=d2*d(k-1)=...=n
互素数有对应关系,gcd(i,n)=gcd(n-i,n)
4.两个相邻奇数互素
5. 满足x%a&&x%b的数字和满足x%ab的数字一一对应
