$ color{#0066ff}{ 题目描述 }$
轻车熟路的 Zayid 顺利地通过了海选,接下来的环节是导师盲选,这一阶段的规则是这样的:
总共 (n) 名参赛选手(编号从 (1) 至 (n) )每人写出一份代码并介绍自己的梦想。接着 由所有导师对这些选手进行排名。为了避免后续的麻烦,规定不存在排名并列的情况。
同时,每名选手都将独立地填写一份志愿表,来对总共 (m) 位导师(编号从 (1) 至 (m) )作出评价。志愿表上包含了共 (m) 档志愿。对于每一档志愿,选手被允许填写最多 (C) 位导师,每位导师最多被每位选手填写一次(放弃某些导师也是被允许的)。
在双方的工作都完成后,进行录取工作。每位导师都有自己战队的人数上限,这意味着可能有部分选手的较高志愿、甚至是全部志愿无法得到满足。节目组对“前 iii 名的录取结果最优”作出如下定义:
- 前 (1) 名的录取结果最优,当且仅当第 (1) 名被其最高非空志愿录取(特别地,如果第 (1) 名没有填写志愿表,那么该选手出局)。
- 前 (i) 名的录取结果最优,当且仅当在前 (i - 1) 名的录取结果最优的情况下,第 (i) 名 被其理论可能的最高志愿录取(特别地,如果第 (i) 名没有填写志愿表,或其所有志愿中的导师战队均已满员,那么该选手出局)。
如果一种方案满足“前 (n) 名的录取结果最优”,那么我们可以简称这种方案是最优的。
举例而言,(2) 位导师 ( m T) 老师、 ( m F) 老师的战队人数上限分别都是 (1) 人;(2) 位选手 Zayid 、DuckD 分列第 (1) 、 (2) 名。那么下面 (3) 种志愿表及其对应的最优录取结果如表中所示:
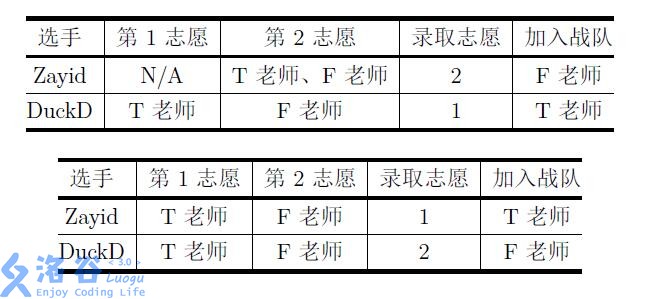
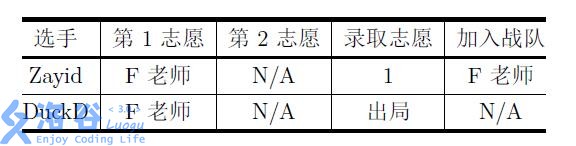
可以证明,对于上面的志愿表,对应的方案都是唯一的最优录取结果。
每个人都有一个自己的理想值 (s_i) ,表示第 (i) 位同学希望自己被第 (s_i) 或更高的志愿录取,如果没有,那么他就会非常沮丧。
现在,所有选手的志愿表和排名都已公示。巧合的是,每位选手的排名都恰好与它们的编号相同。
对于每一位选手,Zayid 都想知道下面两个问题的答案:
- 在最优的录取方案中,他会被第几志愿录取。
- 在其他选手相对排名不变的情况下,至少上升多少名才能使得他不沮丧。
作为《中国新代码》的实力派代码手,Zayid 当然轻松地解决了这个问题。不过他还是想请你再算一遍,来检验自己计算的正确性。
(color{#0066ff}{输入格式})
每个测试点包含多组测试数据,第一行 (2) 个用空格隔开的非负整数 (T,C) ,分别表示数据组数、每档志愿最多允许填写的导师数目。
接下来依次描述每组数据,对于每组数据:
- 第1 行两个用空格隔开的正整数 (n,m) 。
(n,m) 分别表示选手的数量、导师的数量。
- 第 (2) 行 (m) 个用空格隔开的正整数:其中第 (i) 个整数为 (b_i) 。
(b_i) 表示编号为 (i) 的导师战队人数的上限。
第 (3) 行至第 (n + 2) 行,每行 (m) 个用空格隔开的非负整数:其中第 (i + 2) 行左起第 (j) 个数为 (a_{i,j}) 。
(a_{i,j}) 表示编号为 (i) 的选手将编号为 (j) 的导师编排在了第 (a_{i,j}) 志愿。特别地,如果 (a_{i,j}= 0) ,则表示该选手没有将该导师填入志愿表。
在这一部分,保证每行中不存在某一个正数出现超过 (C) 次( (0) 可能出现超过 (C) 次),同时保证所有 (a_{i,j} leqslant m) 。
- 第 (n + 3) 行 (n) 个用空格隔开的正整数,其中第 (i) 个整数为 (s_i) 。
(s_i) 表示编号为 (i) 的选手的理想值。
在这一部分,保证 (s_i leqslant m) 。
(color{#0066ff}{输出格式})
按顺序输出每组数据的答案。对于每组数据,输出 (2) 行:
-
第 (1) 行输出 (n) 个用空格隔开的正整数,其中第 (i) 个整数的意义为:
在最优的录取方案中,编号为i 的选手会被该档志愿录取。
特别地,如果该选手出局,则这个数为 (m + 1) 。
-
第 (2) 行输出 (n) 个用空格隔开的非负整数,其中第 (i) 个整数的意义为:
使编号为 (i) 的选手不沮丧,最少需要让他上升的排名数。
特别地,如果该选手一定会沮丧,则这个数为 (i) 。
(color{#0066ff}{输入样例})
6
1 8 5 10 8
1 6 7 2 6
0 2
0 9
1 4 7 6 7
0 5
(color{#0066ff}{输出样例})
2
0
3
(color{#0066ff}{数据范围与提示})
对于 30%的数据,n ≤ 1000
对于 100%的数据,1 ≤ n ≤ (10^5), 1 ≤ k, x0, x1 ≤ 39989, 1 ≤ y0 ≤ y1 ≤ (10^9)
(color{#0066ff}{题解})
其实就是匈牙利+乱搞qwq
对于每个人,按照志愿顺序匹配,如果那个导师名额没满,显然根据题目,直接选这个志愿就行了
如果满了,那么我们枚举选了这个导师的人, 看能不能让他换导师,自己选这个,这样就可以跑匈牙利了
第一问就这样处理出来了,考虑第二问,对于当前的人,到底哪些人的排名可以对当前的人产生贡献
其实就是这个点在增广的时候,增广路上的排名比它小的人的排名
为什么呢,因为那些人肯定能选他的最优解,那么你在增广路的时候遍历到了他,那你在他的位置肯定能选到你要的导师
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; LL x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
const int maxn = 220;
int f[maxn][maxn][13], g[maxn][maxn], lim[maxn];
int to[maxn], choose[maxn], min[maxn], now, s[maxn], max, n, m;
bool vis[maxn];
bool dfs(int x, int k) {
if(x < now) max = std::max(max, x);
for(int i = 1; i <= g[x][k]; i++) {
int go = f[x][k][i];
if(vis[go]) continue;
vis[go] = true;
if(lim[go]) return lim[go]--, choose[x] = k, to[x] = go, true;
for(int j = 1; j <= n; j++) {
if(j == x || to[j] != go) continue;
if(dfs(j, choose[j])) return to[x] = go, choose[x] = k, true;
}
}
return false;
}
int main() {
int T = in(), x; in();
while(T --> 0) {
n = in(), m = in();
memset(g, 0, sizeof g);
memset(to, 0, sizeof to);
for(int i = 1; i <= m; i++) lim[i] = in();
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++) {
if(!(x = in())) continue;
f[i][x][++g[i][x]] = j;
}
for(int i = 1; i <= n; i++) s[i] = in(), min[i] = i, choose[i] = m + 1;
for(int i = 1; i <= n; i++) {
memset(vis, 0, sizeof vis);
now = i;
for(int j = 1; j <= m; j++) {
if(!g[i][j]) continue;
max = 0;
if(dfs(i, j)) { if(j <= s[i]) min[i] = 0; break; }
if(j <= s[i]) min[i] = std::min(min[i], i - max);
}
}
for(int i = 1; i <= n; i++) printf("%d%c", choose[i], i == n? '
' : ' ');
for(int i = 1; i <= n; i++) printf("%d%c", min[i], i == n? '
' : ' ');
}
return 0;
}