先放图:
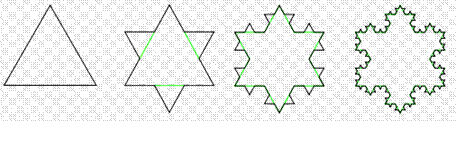
诶?真是奇怪,为啥这些由直线构成的图形叫做曲线呢?
因为这个图形可以无限变换,无数条直线,组合起来不就是一条曲线吗?比如说圆,我们可以说它是曲线图形,也可以说它是正无限多边形。
这个Koch曲线又叫雪花曲线,每一次的变化就是把每一条边,长度变为原来的(frac{4}{3})。
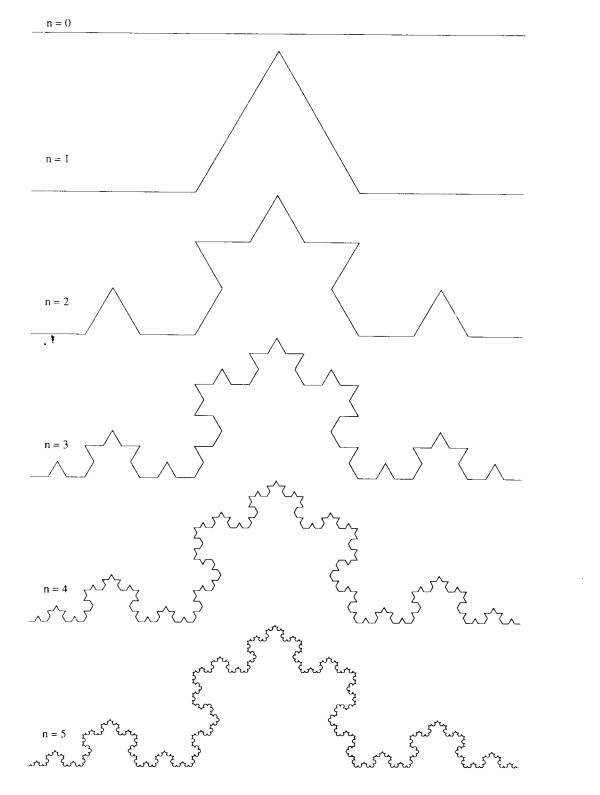
每一次,每条边就从中间凸起一个正三角形,然后周长增加(frac{1}{3})。
然后,我们再来分析一下这个Koch曲线的诡异性质:
性质1:它虽然连续,但是没有切线,不可微。
性质2:它是自相似的,自相似就是指把图形一部分放大,其形状与整体相同。
性质3:它的周长可以无限延长,但是面积始终是收敛的。
好毒瘤的性质啊。
特别是性质3。
为什么它的周长可以无限延长但是面积却可以不超过某个值呢?
先发扬我们Oier的优良传统:推式子
周长:
假设初始的正三角形的周长为(L),那么每经过一次变化,周长就能增加到原来的(frac{4}{3}),,所以说,如果用(L_n)来表示n次变换后的周长,那么当(n oinfty)的时候,周长(L_n oinfty)即(limlimits_{n oinfty}L_n=infty)
面积:
面积的推导有点麻烦,但是如果用上OI中的递推法和一点点小学数学就能推出。
设,(S_n)表示第n个图形的面积,(S)为初始的正三角形面积,易知(S=S_1)
接着往下推导:
(S_2=S_1+3 imes4^0 imes(frac{1}{3})^2S)
(S_3=S_2+3 imes4^1 imes(frac{1}{3})^{2 imes2}S)
(……………………)
(S_n=S_{n-1}+3 imes4^{n-2} imes(frac{1}{3})^{2(n-1)}S)
然后迭代展开,得到:
(S_n=S_1+3 imes4^0 imes(frac{1}{3})^2 S+3 imes4^1 imes(frac{1}{3})^{2 imes2}S+……+3 imes4^{n-2} imes(frac{1}{3})^{2(n-1)}S)
其实这一步在OI中把递归改为了线性递推式。
提取公因式,得:
(S_n=S_1+3S[4^0 imes(frac{1}{3})^2 S+4^1 imes(frac{1}{3})^{2 imes2}+……+4^{n-2} imes(frac{1}{3})^{2(n-1)}])
设中括号中的式子为(A),推导(A):
中括号内的数列为等比数列,首项为((frac{1}{3})^2),公比为(4 imes(frac{1}{3})^2),然后套等比数列的式子,得到
(A=frac{(frac{1}{3})^2 imes {1-[4 imes(frac{1}{3})^2]^{n-1}}}{1-4 imes(frac{1}{3})^2})
然后经过一番计算后(实际上是我懒得打(LaTeX)),推导出来:
(A=frac{1}{5} imes[1-(frac{4}{9})^{n-1}])
然后把(A)带回去,得到:
(S_n=S_1+frac{3}{5}[1-(frac{4}{9})^{n-1}]S)
(∵S_1=S)
(∴S_n={1+frac{3}{5}[1-(frac{4}{9})^{n-1}]}S)
当(n oinfty)时,(S_n=limlimits_{n oinfty}{1+frac{3}{5}[1-(frac{4}{9})^{n-1}]}S)
然后?要求极限了……菜鸡scw数列的极限没学好555……
(S_n=limlimits_{n oinfty}{1+frac{3}{5}[1-(frac{4}{9})^{n-1}]}S)
(={limlimits_{n oinfty}1+limlimits_{n oinfty}frac{3}{5} imeslimlimits_{n oinfty}[1-(frac{4}{9})^{n-1}]}S)
(=S+frac{3}{5} imes[limlimits_{n oinfty}1-limlimits_{n oinfty}(frac{4}{9})^{n-1}]S)
(=S+frac{3}{5} imes(1-0)S)
(=S+frac{3}{5}S)
(=1.6S)
呼~终于推完式子了……
看到了嘛,这个在无限变化后,面积收敛于一开始正三角形面积的1.6倍。
好鬼畜啊qwq
(未完待续qwq)