基础-递归

递归原理

递归是一种解决问题的有效方法，在递归过程中，函数将自身作为子例程调用

你可能想知道如何实现调用自身的函数。诀窍在于，每当递归函数调用自身时，它都会将给定的问题拆解为子问题。

递归调用继续进行，直到到子问题无需进一步递归就可以解决的地步。

为了确保递归函数不会导致无限循环，它应具有以下属性：

一个简单的基本案例（basic case）（或一些案例） —— 能够不使用递归来产生答案的终止方案。---终止条件
一组规则，也称作递推关系（recurrence relation），可将所有其他情况拆分到基本案例。 ---递推关系

注意，函数可能会有多个位置进行自我调用。

示例

让我们从一个简单的编程问题开始：

以相反的顺序打印字符串。

你可以使用迭代的办法轻而易举地解决这个问题，即从字符串的最后一个字符开始遍历字符串。但是如何递归地解决它呢？

首先，我们可以将所需的函数定义为 printReverse(str[0...n-1])，其中 str[0] 表示字符串中的第一个字符。然后我们可以分两步完成给定的任务：

printReverse(str[1...n-1])：以相反的顺序打印子字符串 str[1...n-1] 。
print(str[0])：打印字符串中的第一个字符。

请注意，我们在第一步中调用函数本身，根据定义，它使函数递归。

例子：

private static void printReverse(char [] str) {
  helper(0, str);
}

private static void helper(int index, char [] str) {
  if (str == null || index >= str.length) {
    return;
  }
  // 这可以理解为，先输出当前index之后索引的字符（即index+1），且该方法可以宏观理解为，已经输出后后边所有的字符了，接下来输出当前字符  
  helper(index + 1, str);
  System.out.print(str[index]);
}

递归例子：

一、反转字符串

问题：

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

package com.example.demo;

public class TestString0001 {

    public void reverseString(char[] s) {
        int len = s.length;

        swap(s, 0, len - 1);
    }

    private void swap(char[] s, int left, int right) {
        if (left > right) {
            return;
        }
        char temp = s[left];
        s[left] = s[right];
        s[right] = temp;

        swap(s, left+1, right-1);
    }

    public static void main(String[] args) {

        TestString0001 t = new TestString0001();
        char[] arr = {'H', 'a', 'n', 'n', 'a', 'h'};
        t.reverseString(arr);
        for (char c : arr) {
            System.out.println(c);
        }
    }
}

二、问题

两两交换链表中的节点

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。
你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

class Solution {
    public ListNode swapPairs(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode temp = head;
        head = head.next;
        temp.next = head.next;
        head.next = temp;

        //下一个交换
        head.next.next = swapPairs(head.next.next);
        return head;
    }
}

递推关系：

在实现递归函数之前，有两件重要的事情需要弄清楚:

递推关系：一个问题的结果与其子问题的结果之间的关系。
基本情况: 不需要进一步的递归调用就可以直接计算答案的情况。有时，基本案例也被称为 bottom cases，因为它们往往是问题被减少到最小规模的情况，也就是如果我们认为将问题划分为子问题是一种自上而下的方式的最下层。

一旦我们计算出以上两个元素，再想要实现一个递归函数，就只需要根据递推关系调用函数本身，直到其抵达基本情况。

为了解释以上几点，让我们来看一个经典的问题，帕斯卡三角（Pascal's Triangle）:

帕斯卡三角形是排列成三角形的一系列数字。在帕斯卡三角形中，每一行的最左边和最右边的数字总是 1。对于其余的每个数字都是前一行中直接位于它上面的两个数字之和。

下面的插图给出了一个 5 行的帕斯卡三角：

Pascal_Triangle

根据上面的定义，我们生成一个具有确定行数的帕斯卡三角形。

帕斯卡三角的递推关系：

首先，我们定义一个函数

我们可以用下面的公式来表示这一递推关系：

因此，我们可以将基本情况定义如下:

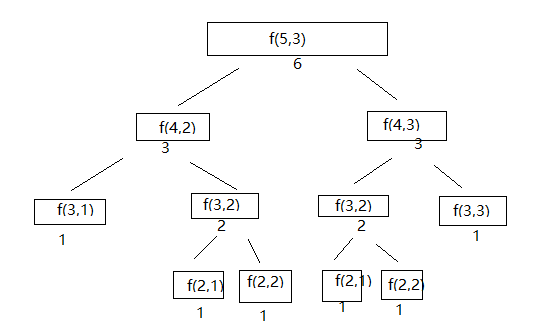
在上边可以观察到，递归会产生一些重复计算问题

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]

class Solution {
       /**
     * 杨辉三角输出 递归方式（该问题也属于基本的动态规划问题，可以使用动态规划方法解答）
     * 最左边和最右边都为1，且j<=i，
     * f(i,j)：第i行第j列的数字，当i=1 时，f(1,j) = 1,当i==j时，f(i,j) = 1;其他情况，f(i,j) = f(i-1,j-1) + f(i-1,j)
     *
     * @param numRows
     * @return
     */
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> res = new ArrayList<>();
        if(numRows == 0){
            return res;
        }

        digui(res, 1, numRows);
        return res;
    }

    public void digui(List<List<Integer>> list, int cur, int numRows) {
        if (cur > numRows) {
            return;
        }

        List<Integer> curList = new ArrayList<>();
        for (int i = 1; i <= cur; i++) {
            if (i == 1 || i == cur) {
                curList.add(1);
            } else {
                List<Integer> pre = list.get(cur - 2);
                int s = pre.get(i - 2) + pre.get(i-1);
                curList.add(s);
            }
        }
        list.add(curList);

        digui(list, cur + 1, numRows);

    }
}