约瑟夫环

1. 报数，删除报到k的人，直到只剩下一个人

题目：已知n个人（以编号1，2，3...n分别表示）围坐在一张圆桌周围。从编号为1的人开始报数，数到m的那个人出列；他的下一个人又从1开始报数，数到m的那个人又出列；依此规律重复下去，直到圆桌周围的人全部出列。通常，我们会要求输出最后一位出列的人的序号。那么这里主要研究的是最后一个出列的人的序号要怎么确定。

首先，数组写成以0开头更便于计算，所以后面的分析都是以0开头的。

分析：

举个栗子：总人数sum为10人，从0开始，每报到4就把一人扔下去（value=4）。

初始情况为:　　　0 1 2 3 4 5 6 7 8 9

扔下去一个之后:　0 1 2 4 5 6 7 8 9

此时，这些编号已经不能组成一个环，但是可以看出4至2之间还是连着的（4 5 6 7 8 9 0 1 2），且下一次报数将从4开始。但是，之后的报数将总要考虑原编号3处的空位问题。

如何才能避免已经产生的空位对报数所造成的影响呢？

可以将剩下的9个连续的数组成一个新的环（将2、4连接），这样报数的时候就不用在意3的空位了。但是新产生的环的数字并非连续的，报数时不像之前那样好处理了（之前没人被扔海里时下一个报数的人的编号可以递推，即(当前编号+1)%sum ），无法不借助存储结构得知下一个应该报数的现存人员编号。

如何使新环上的编号能够递推来简化我们之后的处理呢？

可以建立一种有确定规则的映射，要求映射之后的数字可以递推，且可以将在新环中继续按原规则报数得到的结果逆推出在旧环中的对应数字。

方法：将它与 sum-1 个人组成的（0 ~ sum-1）环一一映射。

比如之前的栗子，将剩余的 9 人与 9 人环（0~8）一一映射

既然 3 被扔到海里之后，报数要从4开始（4 其实在数值上等于最大报数值），那么就将4映射到0~8的新环中0的位置，也就是说在新环中从0开始报数即可，且新环中没有与3对应的数字，因此不必担心有空位的问题。从旧环的 4 开始报数等效于从新环中的 0 开始报数。

原始 0 1 2 3 4 5 6 7 8 9

旧环 0 1 2 4 5 6 7 8 9

新环 6 7 8 0 1 2 3 4 5

新环有这么一个优势: 相比于旧环中2与4之间在数学运算上的不连续性，新环8和0之间在对9取余的运算中是连续的，也就是说根本不需要单独费心设计用以记录并避开已产生的空位（如编号3）的机制，新环的运算不受之前遗留结果的掣肘。同时只要能将新环与旧环的映射关系逆推出来，就能利用在新环中报数的结果退出之前旧环中的报数结果。

以下是新环与旧环中下一个要人扔海里的人位置:

旧环 0 1 2 4 5 6 7 8 9

新环 6 7 8 0 1 2 3 4 5

如何由新环中的 3 得到旧环中的 7 呢。其实可以简单地逆推回去 : 新环是由 (旧环中编号-最大报数值)%旧总人数 得到的，所以逆推时可以由 ( 新环中的数字 + 最大报数值 )% 旧总人数 取得。即 old_number = ( new_number + value ) % old_sum.

如 : ( 3 + 4 ) % 10 =7 .

也就是说在，原序列( sum ) 中第二次被扔入海中编号可以由新序列( sum - 1) 第一次扔海里的编号通过特定的逆推运算得出。

而新序列 (sum -1)也是（从0开始）连续的，它的第二次被扔入海中的编号由可以由（sum - 2）的第一次扔入海里的编号通过特定的逆推运算得出，并且它的第二次被扔入海中的编号又与原序列中的第三次被扔入海里的编号是有对应关系的。

也求是说有以下推出关系: (sum-2)环的第1次出环编号 >>>(sum-1)环的第2次出环编号 >>>(sum)环的第3次出环编号

即在以 k 为出环报数值的约瑟夫环中， m人环中的第n次出环编号可以由 (m-1) 人环中的第 (n-1) 次出环编号通过特定运算推出。

幸运的是，第一次出环的编号是可以直接求出的，也就是说，对于任意次出环的编号，我们可以将之一直降到第一次出环的编号问题，再一一递推而出。

注意以下图示中的环数字排列都是顺序的，且从编号0开始。

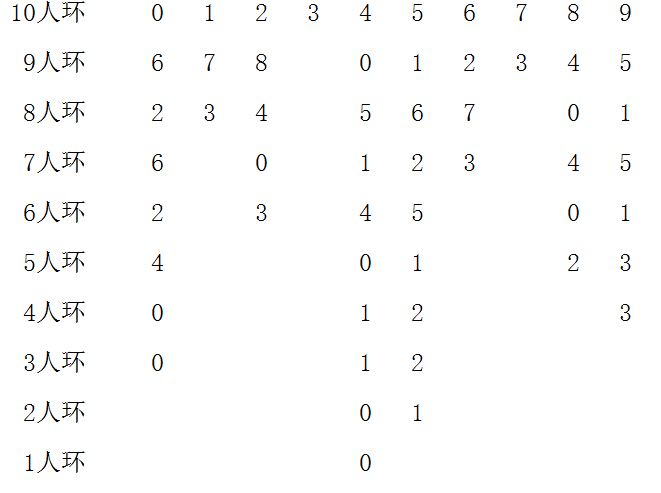
由图知，10人环中最后入海的是4号，现由其在1人环中的对应编号0来求解。

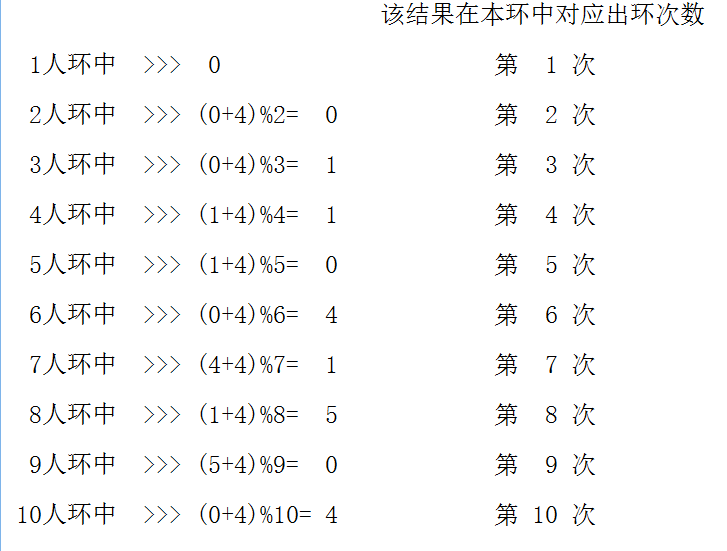
　　通过以上运算，其实我们已经求出分别位于9个环中九个特定次数的结果，只不过我们需要的是10人环的结果罢了。

　　这种方法既可以写成递归也可以写成循环，它对于求特定次数的出环编号效率较高。递归就比较好写了，出口即是当次数为1时。实际编号是从1开始，而不是0，输出时要注意转换

代码1：

def lastRemaining(n,m):
    if n < 1:
        return -1
    con = list(range(n))
    final = -1
    start = 0
    while con:
        k = (start+m-1)%n
        final = con.pop(k)
        n -= 1
        start = k
    return final
    
res = lastRemaining(10,4)
print(res)

代码2: 一共有三十个人，从1-30依次编号。每次隔9个人就踢出去一个人。求踢出的前十五个人的号码：

a = [ x for x in range(1,31) ] #生成编号
del_number = 8 #该删除的编号
for i in range(15):
   print a[del_number]
   del a[del_number]
   del_number = (del_number + 8) % len(a)

2. 按递增间隔删数，直到最后只剩下一个数

题目：有数组A，每个元素存放相应的下标,即A[i]=i，要求按照1,2,3,...的规律删除数组中的元素,第一次间隔1个数，第二次间隔2个数,依次类推，到末尾时循环至开头继续进行,求最后一个被删掉的数的原始下标位置

思路：

count用来记录要删除的数在数组中的下标，num是要删除的间隔

step1：删除第一个元素，num=1，count=1，删除1

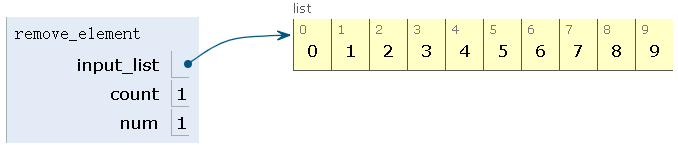
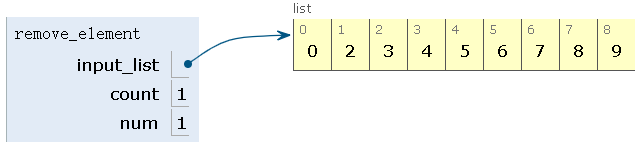
step2：删除第二个元素，num=2，count=1+2=3，删除4

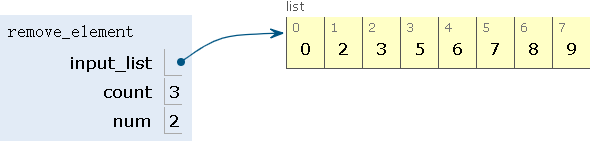
step3：删除第三个元素，num=3，count=3+3=6，删除8

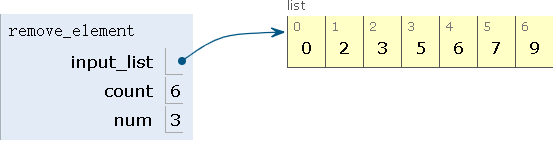
step4：删除第四个元素，num=4，count=6+4=10>7,count=10%7=3，删除5

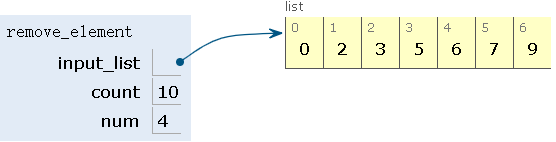
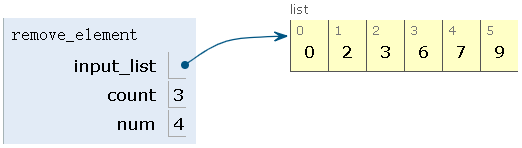
step5：删除第五个元素，num=5，count=3+5=8>7,count=8%6=2,删除3

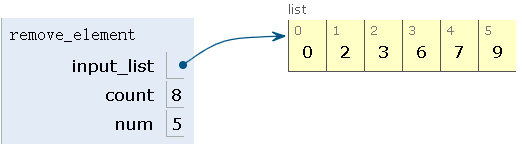
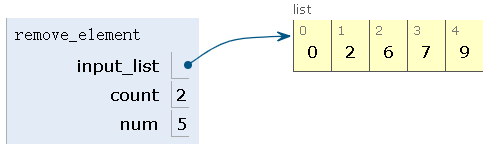
step6：删除第六个元素，num=6，count=2+6=8>5,count=8%5=3,删除7

step7：删除第七个元素，num=7，count=3+7=10>4,count=10%4=2,删除6

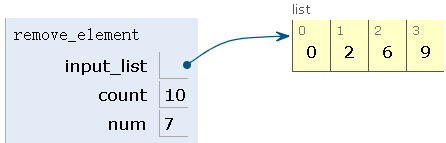
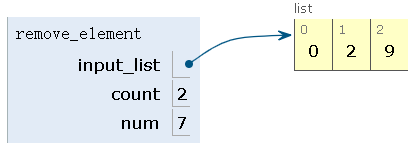
step8：删除第八个元素，num=8，count=2+8=10>3,count=10%3=1,删除2

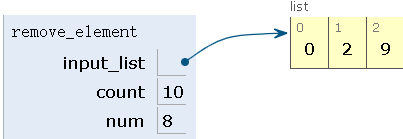
step9：删除第九个元素，num=9，count=1+9=10>2,count=10%2=0,删除0

代码如下：

def remove_element(input_list):
    count = 0
    num = 0
    while len(input_list) != 1:
        num += 1#间隔1,2,3,...直到只剩下一个数
        count = count + num#1 3 6 10 15% 21 28 36
        #按间隔排的数1,3,6,10,8,8,10,10,10---1,3,6,3,2,3,2,1,0
        # print('count=%s'%count)
        if count >= len(input_list):
            count = count % len(input_list)
        print('count=%s,删除%s'%(count,input_list[count]))
        input_list.pop(count)
    print(input_list[0])

remove_element([0,1,2,3,4,5,6,7,8,9])

最后剩下的数为9

参考文献：

【4】约瑟夫环问题