我们来看一个场景, 假设您有一个未排序的列表。您想知道列表中是否存在一个数量占列表的总数一半以上的元素, 我们称这样一个列表元素为 Majority 元素.如果有这样一个元素, 求出它?如果没有,你需要知道没有。你想要尽可能高效地完成这个工作。
这个问题的一个常见场景可能是容错计算, 您执行多个冗余计算,然后验证大多数结果是否一致。
Majority Element
Boyer-Moore 算法在 Boyer-Moore Majority Vote Algorithm 中提出。该算法使用 O(1) 额外空间和 O(N) 时间。它只需要遍历输入列表中 2 遍。实现这一点也很简单,虽然有点麻烦来了解它的工作原理。
算法描述
第一次遍历列表,会生成 Majority 元素的候选值。 第二遍只是计算该元素的频数以确认是否是 Majority 元素。
在第一次遍历列表时,我们需要记录 2 个值:
- candidate, Majority候选值, 可初始化为任何值。
- count, 候选值净获取的投票计数(总支持-总反对票), 初始化为0。
算法流程
对于输入列表中的每个元素,我们首先判断当前元素是不是等于候选值。
- 如果当前元素等于候选值, 计数器加1, continue
- 如果当前元素不等与候选值, 检查计数器
- 如果计数器等于0, 令当前元素为候选值, 计数器设置为1, continue
- 如果计数器不为0, 计数器减一, continue
def majority(nums):
candidate = 0
cnt = 0
# 第 1 次遍历
for value in nums:
if candidate == value:
cnt += 1
elif cnt != 0:
cnt -= 1
else:
candidate, cnt = value, 1
# 第 2 次遍历
maj = nums.count(candidate)
if maj > len(nums) / 2:
return maj
第 1 次遍历结束时,如果存在 Majority,候选值将是 Majority。
第 2 次历可以验证候选值 candidate 是否是 Majority。
算法解析
为了看这是如何工作的,我们只需要考虑包含 Majority 的情况。如果该列表不包含 Majority 元素,则第二次遍历会轻易地拒绝该候选者。
首先,考虑第一个元素不是 Majority 元素的列表,例如,Majority为 0 的列表:
[5,5,0,0,0,5,0,0,5]
当处理第一个元素时,我们将 5 分配给候选值,计数器初始化为 1。由于 5 不是 Majority,在遍历到列表的最后一个元素之前的某个时刻,count 将会下降到 0。在上面的例子中,这发生在第 4 个元素:
列表值:
[5,5,0,0,...
计数值:
[1,2,1,0,...
在计数返回到 0 的时候,我们已经消耗了和元素 5 相同数量的其他元素。如果所有其他元素都是这种情况下的 Majority 元素,那么我们已经消耗了 2 个 Majority 元素和 2 个非 Majority 元素。这是我们可以消费的最多的Majority元素,但即使这样, Majority 元素仍然是输入列表剩余部分的大部分(在我们的示例中,余数为... 0,5,0,0,5])。
(color{red}{关键思想})
如果第一个元素是 Majority 元素,并且在某个时间点计数器下降到 0,那么我们还可以看到,多数元素仍然是输入列表剩余部分的大部分,因为我们消耗了相等数的 Majority 元素和非 Majority 元素。我们可以一遍又一遍地重复地抛弃我们前面输入的范围,直到找到一个范围,该范围是以 Majority 元素开头且 count 计数器不会降到 0.
如果第一个元素不是 Majority 元素, 那么该元素可能消耗 Majority 也可能消耗非 Majority 元素, 那么多数元素仍然是输入列表剩余部分的大部分
(color{red}{所以, 列表中的元素的排列顺序不影响我们算法执行的最终结果.}), 不妨假设 Majority 元素都排在列表的首部
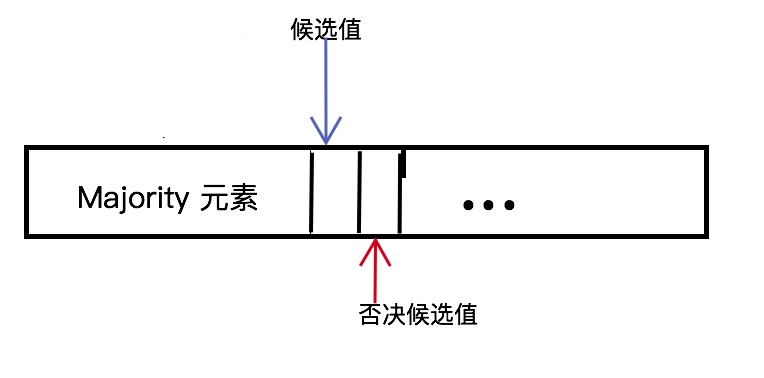 

因此,如果 Majority 如果存在, 候选值必须是该列表的 Majority,并且是输入列表中的 Majority 的唯一可能的候选值.
Majority Element II
给定一个大小为 n 的整数数组,找到所有出现次数超过 (lfloor frac{1}{3} floor) 次的元素。该算法在线性时间 O(n) 和额外的 O(1) 空间复杂度内完成计算
思路: 首先就是看看列表中最多会有几个这样的 Majority 元素, 由于这里的 Majority 元素的为频数大于 (lfloor frac{1}{3} floor), 所以这样的元素最多有 2 个. 下面是 Most voted Solution, 灵活的使用的了 Boyer-Moore Voted Algorithm.
def majority(nums):
if not nums:
return []
# 这里 candidate1 和 candidate2 设置为不同值为了
# 防止Majority 就等于 candidate1 或 candidate2,
# 那么如果只有一 Majority, 那么却返回两个相同的, 所以要初始化为不同值
count1, count2, candidate1, candidate2 = 0, 0, 0, 10
# 第一轮循环
for n in nums:
if n == candidate1:
count1 += 1
elif n == candidate2:
count2 += 1
elif count1 == 0:
candidate1, count1 = n, 1
elif count2 == 0:
candidate2, count2 = n, 1
else:
count1, count2 = count1 - 1, count2 - 1 # 1个同时否决两个, 很重要
# 第二轮循环
res = [n for n in (candidate1, candidate2) if nums.count(n) > len(nums) // 3]
return res
共有有 3 种情况:
- 列表没有 Majority 元素, 那么第一轮选出的候选值在第二轮都会被淘汰
- 列表只有 1 个 Majority 元素, 那么第一轮选出的 2 个候选值中会有 1 个在第二轮都会被淘汰
- 列表有 2 个 Majority 元素, 那么第一轮选出的 2 个候选值都是 Majority
第 1 种情况
由于列表没有 Majority 元素, 自然没有元素的频数大于 (lfloor frac{1}{3} floor), 第二轮 2 个候选值都会被淘汰. 难缠的是第 2 种情况, 所以放在最后, 下面先说第 3 种情况
第 2 种情况
如果只有 1 个 Majority 元素,
列表只有 1 个 Majority 元素, 数量是超过列表元素的 (frac{1}{3}), 那么非 Majority 元素的数量可能大于总数的 (frac{1}{2}), 那我们选择的候选值中会包括 Majority 元素吗?
假设非 Majority 元素不会相互取消投票, 所有的非 Majority 元素都用来否决 Majority 的投票. 那么非 Majority 在否决 Majority 的同时也会否决另一个 非 Majority, 也就是说想要否决超过总数 (frac{1}{3}) 的 Majority 需要超过总数 (frac{2}{3}) 的非 Majority 元素, 这是不可能的, 所以 Majority 元素一定会成为候选者之一.
在第二轮循环中, 通过奇数排除 非Majority元素, 搞定
第 3 种情况
首先, 我们先考虑会不会出现两个 Majority 相互取消彼此投票的可能 ?
如果有两个 Majority 元素, 那么非 Majority 元素的数量少于总数的 (frac{1}{3})
假设两个 Majority 元素分别为 Majority A 和 Majority B, Majority A 为当前候选值之一, 如果 Majority B 要取消 Majority A 的投票, 那么一定还会取消另一个非 Majority 元素的投票, 又由于 非 Majority 元素的数量少于总数的 (frac{1}{3}), 那么最后 Majority B 一定会成为候选者之一.
(候选者还会取消彼此的投票, 这时候更不可能有非 Majority 元素成为候选者之一)