使用《python数据分析与数据化运营》一书的代码及数据。
用决策树做分类:
#导入库
import numpy as np import pandas as pd from sklearn import tree #导入决策树库 import prettytable #导入表格库 import matplotlib.pyplot as plt #导入图形展示库 import pydotplus #导入dot插件库 from sklearn.model_selection import train_test_split #数据分区库,用于数据将数据分为训练集、测试集 from sklearn.metrics import confusion_matrix,accuracy_score,auc,f1_score,precision_score,recall_score,roc_curve #导入指标库
#导入数据
df=pd.read_csv(r'E:data analysis estclassification.csv')
#输出数据整体信息
print('samples:%d features:%d' % (x.shape[0],x.shape[1])) #整体数据的信息,一共有多少个样本,多少个特征
print(70*'-')
samples:21927 features:4
#分割数据
x=df.ix[:,:-1] #分割x y=df.ix[:,-1] #分割y x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=0)
#将数据分为训练集,测试集,设置random_state等于固定的值,则每次得到的训练集是一样的、测试集也是一样的
train_test_split(train_data,train_target,test_size, random_state):用于分割数据集
参数:
train_data:所要划分的样本特征集,即x
train_target:所要划分的样本结果,即y
test_size:测试集的占比,如果是整数的话就是样本的数量。
random_state:是随机数的种子。种子不同,产生不同的随机数;种子相同,即使实例不同也产生相同的随机数。
#训练分类模型
model_tree=tree.DecisionTreeClassifier(random_state=0) #建立决策树模型对象。决策树的生成过程中,往往引入随机数,这是为了得到更好的分类间隔。如数据本身的特征是连续的,计算分割点就需要随机。 model_tree.fit(x_train,y_train) #将训练集导入模型 pre_y=model_tree.predict(x_test) #将测试集的x导入建好的决策树模型,得出测试集的y
#计算混淆矩阵,用于评价决策树
confusion_m=confusion_matrix(y_test,pre_y) #获得混淆矩阵 confusion_table=prettytable.PrettyTable() #创建表格 confusion_table.add_row(confusion_m[0,:]) #将混淆矩阵的第一行添加到表格的第一行 confusion_table.add_row(confusion_m[1,:]) #将混淆矩阵的第二行添加到表格的第二行 print(confusion_table)
+---------+---------+
| Field 1 | Field 2 |
+---------+---------+
| 5617 | 282 |
| 321 | 359 |
+---------+---------+
#从准确率(accuracy)、精确度(precision)、召回率(recall)、F1得分值,AUC(ROC曲线下的面积),这5个指标评价决策树
accuracy_s=accuracy_score(y_test,pre_y) #计算准确度 precision_s=precision_score(y_test,pre_y) #计算精确度 recall_s=recall_score(y_test,pre_y) #计算召回率 f1_s=f1_score(y_test,pre_y) #计算F1得分
y_score=model_tree.predict_proba(x_test) #获得决策树的预测概率,predict_proba返回的是一个 n 行 k 列的数组, 第 i 行 第 j 列上的数值是模型预测 第 i 个预测样本为某个标签的概率,并且每一行的概率和为1。 fpr,tpr,thresholds=roc_curve(y_test,y_score[:,1]) auc_s=auc(fpr,tpr) #计算AUC
core_metrics=prettytable.PrettyTable() #创建表格 core_metrics.field_names=['auc','accuracy','precision','recall','f1'] #定义表格列名 core_metrics.add_row([auc_s,accuracy_s,precision_s,recall_s,f1_s]) #增加数据 print(core_metrics)
+---------------+----------------+----------------+----------------+----------------+
| auc | accuracy | precision | recall | f1 |
+---------------+----------------+----------------+----------------+----------------+
| 0.75004437442 | 0.908344733242 | 0.560062402496 | 0.527941176471 | 0.543527630583 |
+---------------+----------------+----------------+----------------+----------------+
混淆矩阵:

ture positive(TP):本来是正例,分类成正例
false positive(FP):本来是负例,分类成正例
false negative(FN):本来是正例,分类成负例
true negative(TN):本来是负例,分类成负例
准确度(accuracy):A=(TP+TN)/(TP+FP+FN+TN),取值范围 [0,1],值越大说明分类结果越准确。
精确度(precision):P=TP/(TP+FP),取值范围 [0,1],值越大说明分类结果越准确。
召回率(recall):R=TP/(TP+FN),取值范围 [0,1],值越大说明分类结果越准确。
F1得分:是准确度和召回率的调和均值,F1=2*(P*R)/(P+R),取值范围 [0,1],值越大说明分类结果越准确。
ROC曲线:
ROC观察模型正确地识别正例的比例与模型错误地把负例数据识别成正例的比例之间的权衡。TPR的增加以FPR的增加为代价。AUC(Area under roccurve),即ROC曲线下的面积,是模型准确率的度量。
纵坐标:真正率(True Positive Rate , TPR)或灵敏度(sensitivity)
TPR = TP /(TP + FN) (正样本预测结果数 / 正样本实际数)
横坐标:假正率(False Positive Rate , FPR)
FPR = FP /(FP + TN) (被预测为正的负样本结果数 /负样本实际数)
如何画ROC 曲线,对于一个特定的分类器和测试数据集,显然只能得到一个分类结果,即一组FPR和TPR结果,而要得到一个曲线,我们实际上需要一系列FPR和TPR的值。分类器的一个重要功能“概率输出”,即表示分类器认为某个样本具有多大的概率属于正样本(或负样本)。阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。
AUC的取值
AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
#图形显示ROC曲线
plt.plot(fpr,tpr,label='ROC') plt.plot([0,1],[0,1],linestyle='--',color='k',label='random chance') #画随机状态下的准确率线 plt.xlabel('false positive rate') #x轴标签 plt.ylabel('true positive rate') #y轴标签 plt.legend(loc='best') #图例,图例位于best位置 plt.show()
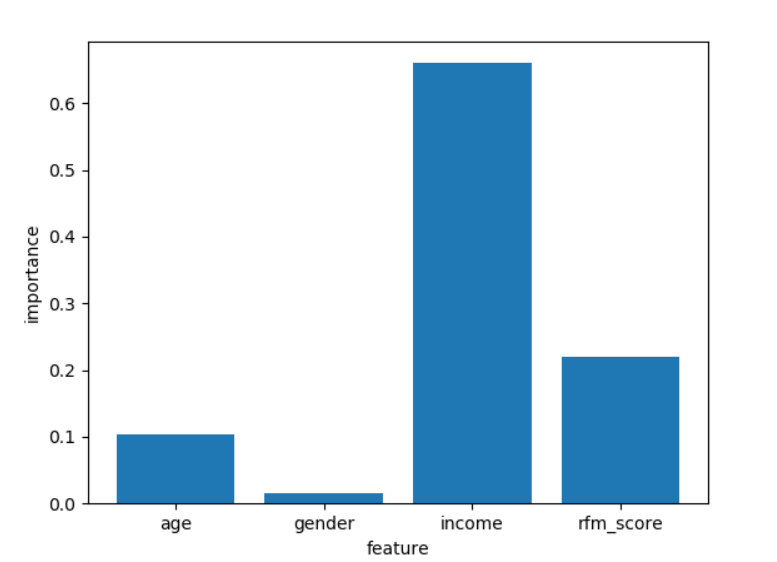
#画出指标的重要性
names_list=['age','gender','income','rfm_score'] #定义特征值的名称(就是x的名称)
feature_importance=model_tree.feature_importances_ #从决策树中获取指标重要性
plt.bar(np.arange(feature_importance.shape[0]),feature_importance,tick_label=names_list) #画出柱状图
plt.xlabel('feature')
plt.ylabel('importance')
plt.show()
#模型应用
x_new=pd.DataFrame([[40,0,55616,0],[17,0,55568,0],[55,1,55932,1]]) y_pre_new=model_tree.predict(x_new) print(y_pre_new)
#将决策树图保存为pdf文件
dot_data=tree.export_graphviz(model_tree,out_file=None,max_depth=5,feature_names=names_list,filled=True,rounded=True) #将决策树生成dot对象 graph=pydotplus.graph_from_dot_data(dot_data) #通过pydotplus将决策树规则解析为图形 graph.write_pdf('tree.pdf') #将决策树规则保存为图形
参考:
http://www.dataivy.cn/blog/classification_with_skelarn_tree/#more-655
http://alexkong.net/2013/06/introduction-to-auc-and-roc/
https://blog.csdn.net/tanzuozhev/article/details/79109311